- Research Article
- Open access
- Published:
Positive Solutions for Boundary Value Problems of 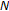 -Dimension Nonlinear Fractional Differential System
-Dimension Nonlinear Fractional Differential System
Boundary Value Problems volume 2008, Article number: 437453 (2009)
Abstract
We study the boundary value problem for a kind  -dimension nonlinear fractional differential system with the nonlinear terms involved in the fractional derivative explicitly. The fractional differential operator here is the standard Riemann-Liouville differentiation. By means of fixed point theorems, the existence and multiplicity results of positive solutions are received. Furthermore, two examples given here illustrate that the results are almost sharp.
-dimension nonlinear fractional differential system with the nonlinear terms involved in the fractional derivative explicitly. The fractional differential operator here is the standard Riemann-Liouville differentiation. By means of fixed point theorems, the existence and multiplicity results of positive solutions are received. Furthermore, two examples given here illustrate that the results are almost sharp.
1. Introduction
We are interested in the following  -dimension nonlinear fractional differential system:
-dimension nonlinear fractional differential system:

that is subject to the boundary conditions

where  is the standard Riemann-Liouville fractional derivative of order
is the standard Riemann-Liouville fractional derivative of order 



 , and
, and  ,
, 

Recently, fractional differential equations (in short FDEs) have been studied extensively. The motivation for those works stems from both the development of the theory of fractional calculus itself and the applications of such constructions in various sciences such as physics, mechanics, chemistry, engineering, and so on. For an extensive collection of such results, we refer the readers to the monographs by Samko et al. [1], Podlubny [2], Miller and Ross [3], and Kilbas et al. [4].
Some basic theory for the initial value problems of FDE involving Riemann-Liouville differential operator has been discussed by Lakshmikantham [5–7], El-Sayed et al. [8, 9], Diethelm and Ford [10], and Bai [11], and so on. Also, there are some papers which deal with the existence and multiplicity of solutions for nonlinear FDE boundary value problems (in short BVPs) by using techniques of topological degree theory. For example, Su [12] considered the BVP of the coupled system

By using the Schauder fixed point theorem, one existence result was given.
In [13], Bai and Lü obtained positive solutions of the two-point BVP of FDE

by means of Krasnosel'skii fixed point theorem and Leggett-Williams fixed point theorem.  is the standard Riemann-Liouville fractional derivative.
is the standard Riemann-Liouville fractional derivative.
Zhang discussed the existence of solutions of the nonlinear FDE

with the boundary conditions


in [14, 15], respectively. Since conditions (1.6) and (1.7) are nonzero boundary values, the Riemann-Liouville fractional derivative  is not suitable. Therefore, the author investigated the BVPs (1.5)-(1.6) and (1.5)–(1.7) by involving in the Caputo fractional derivative
is not suitable. Therefore, the author investigated the BVPs (1.5)-(1.6) and (1.5)–(1.7) by involving in the Caputo fractional derivative  .
.
From above works, we can see a fact, although the BVPs of nonlinear FDE have been studied by some authors, to the best of our knowledge, higher-dimension fractional equation systems are seldom considered. Su in [12] studied the two-dimension system, however, the Schauder fixed point theorem cannot ensure the solutions to be positive. Since only positive solutions are useful for many applications, we investigate the existence and multiplicity of positive solutions for BVP (1.1)-(1.2) in this paper. In addition, two examples are given to demonstrate our results.
2. Preliminaries
For the convenience of the reader, we first recall some definitions and fundamental facts of fractional calculus theory, which can be found in the recent literatures [1–4].
Definition 2.1.
The fractional integral of order  of a function
of a function  is given by
is given by

provided that the integral exists, where  is the Euler gamma function defined by
is the Euler gamma function defined by

for which, the reduction formula

the Dirichlet formula

hold.
Definition 2.2.
The fractional derivative of order  of a continuous function
of a continuous function  can be written as
can be written as

where  denotes the integer part of
denotes the integer part of  , provided that the right side is pointwise defined on
, provided that the right side is pointwise defined on  .
.
Remark 2.3.
The following properties are useful for our discussion:

In the following, we present the useful lemmas which are fundamental in the proof of our main results.
Lemma 2.4 (see [16]).
Let  be a convex subset of a normed linear space
be a convex subset of a normed linear space  and
and  be an open subset of
be an open subset of  with
with  . Then every compact continuous map
. Then every compact continuous map  has at least one of the following two properties:
has at least one of the following two properties:
(A1) has a fixed point;
has a fixed point;
(A2)there is an  with
with  for some
for some  .
.
Definition 2.5.
The map  is said to be a nonnegative continuous concave functional on a cone
is said to be a nonnegative continuous concave functional on a cone  of a real Banach space
of a real Banach space  provided that
provided that  is continuous and
is continuous and

for all  and
and  .
.
Let  and
and  be nonnegative continuous convex functionals on the cone
be nonnegative continuous convex functionals on the cone  ,
,  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on  . Then for positive real numbers
. Then for positive real numbers  and
and  , one defines the following convex sets:
, one defines the following convex sets:

The assumptions below about the nonnegative continuous convex functionals  ,
,  will be used as follows:
will be used as follows:
(B1)there exists  such that
such that  for all
for all  ;
;
(B2) for all
for all  .
.
Lemma 2.6 (see [17]).
Let  be a cone in a real Banach space
be a cone in a real Banach space  ,
,  , and
, and  . Assume that
. Assume that  and
and  are nonnegative continuous convex functionals satisfying (B1) and (B2),
are nonnegative continuous convex functionals satisfying (B1) and (B2),  is a nonnegative continuous concave functional on
is a nonnegative continuous concave functional on  such that
such that  for all
for all  and
and  is a completely continuous operator. Suppose
is a completely continuous operator. Suppose
(C1) ,
,  , for
, for  ;
;
(C2) ,
,  , for all
, for all  ;
;
(C3) for all
for all  with
with  .
.
Then  has at least three fixed points
has at least three fixed points  with
with

3. Related Lemmas
Let  with the norm
with the norm

where  ,
,  with
with

where  is the standard sup norm of the space
is the standard sup norm of the space  . Throughout, we denote
. Throughout, we denote  and
and  . Then
. Then  is a Banach space (see [12]).
is a Banach space (see [12]).
Define the cone  by
by

Lemma 3.1.
If  , then
, then  ,
,  .
.
Proof.
For  , we have
, we have

That is,  ,
,  .
.
It is well known that the solution for the system BVP (1.1)-(1.2) is equivalent to the fixed point of the following integral system:

for  , where
, where

Denote  , we can see
, we can see

 . For the Green functions
. For the Green functions  ,
,  , we can obtain
, we can obtain
(i) for
for  ,
,  for
for  ,
,  , where
, where

here,  is the unique solution of the equation
is the unique solution of the equation

(ii) and
and  .
.
Lemma 3.2.
 is completely continuous.
is completely continuous.
Proof.
We divide the proof into three steps.
Step 1.
 . In fact, for any
. In fact, for any  , since
, since  for
for  and
and  for
for  ,
,  for
for  . Moreover,
. Moreover,  implies that
implies that  .
.
Step 2.
 is continuous on
is continuous on  , which is valid due to the continuity of the function
, which is valid due to the continuity of the function  .
.
Step 3.
We will show that  is relatively compact. For any given bounded set
is relatively compact. For any given bounded set  , there exists
, there exists  such that
such that  for all
for all  . We take
. We take  For
For  , let
, let  be such that
be such that  , we have
, we have

Notice that

one gets

where  , we can see that
, we can see that  is an equicontinuous set. Now, we proof that
is an equicontinuous set. Now, we proof that  is uniformly bounded. For any
is uniformly bounded. For any  ,
,

where  . That is,
. That is,  is uniformly bounded. Thus,
is uniformly bounded. Thus,  is relatively compact. By means of the Arzela-Ascoli theorem,
is relatively compact. By means of the Arzela-Ascoli theorem,  is completely continuous.
is completely continuous.
4. The Existence of One Positive Solution
Theorem 4.1.
If there exist  ,
,  satisfying
satisfying

such that

Then the BVP (1.1)-(1.2) has at least one positive solution.
Proof.
Lemma 3.2 indicates that  is completely continuous.
is completely continuous.
For  , let
, let

Define  , then
, then  . For
. For  ,
,  . Thus,
. Thus,  and
and  :
:

indicate that  , and then
, and then  . Take
. Take  in Lemma 2.4, for any
in Lemma 2.4, for any  ,
,  does not hold. Hence, the operator
does not hold. Hence, the operator  has at least a fixed point, then the BVP (1.1)-(1.2) has at least one positive solution.
has at least a fixed point, then the BVP (1.1)-(1.2) has at least one positive solution.
Example 4.2.
Consider the problem

where

Choose

It is easy to check that (4.1) holds. Thus, by Theorem 4.1, the BVP (4.5) has at least one positive solution. In fact,  is such a solution.
is such a solution.
5. The Existence of Triple Positive Solutions
Let the nonnegative continuous convex functionals  ,
,  and the nonnegative continuous concave functional
and the nonnegative continuous concave functional  be defined on the cone
be defined on the cone  by
by

Obviously,  and
and  satisfy (B1) and (B2),
satisfy (B1) and (B2),  for all
for all  .
.
For simplicity, we denote

Theorem 5.1.
Assume that there exist constants  such that
such that  for
for  . Suppose
. Suppose
(H1) ,
,  ;
;
(H2) ,
,  ;
;
(H3) ,
,  ;
;
(H4) ,
, 
Then the BVP (1.1)-(1.2) has at least three positive solutions  ,
,  and
and  such that
such that

Proof.
Lemma 3.2 has showed that  is completely continuous. Now, we will verify that all the conditions of Lemma 2.6 are satisfied. The proof is based on the following steps.
is completely continuous. Now, we will verify that all the conditions of Lemma 2.6 are satisfied. The proof is based on the following steps.
Step 1.
We will show that (H1) implies  .
.
In fact, for  ,
,  ,
,  , and then
, and then  ,
,  ,
,  . In view of (H1), we have
. In view of (H1), we have

Then  and
and  , that is,
, that is,  .
.
Step 2.
To check the condition (C1) in Lemma 2.6, we choose 
 ,
,  . It is easy to see that
. It is easy to see that

Consequently,  . For any
. For any  , from (H2), one gets
, from (H2), one gets

then we can obtain  .
.
Step 3.
It is similar to Step 1 that we can prove  by condition (H3), that is, (C2) in Lemma 2.6 holds.
by condition (H3), that is, (C2) in Lemma 2.6 holds.
Step 4.
We verify that (C3) in Lemma 2.6 is satisfied. For  with
with  , we have
, we have

Thus,  , (C3) in Lemma 2.6 is satisfied.
, (C3) in Lemma 2.6 is satisfied.
Therefore, the operator  has three points
has three points  with
with

Then the BVP (1.1)-(1.2) has three positive solutions  such that
such that

Example 5.2.
Consider the problem

where

Here, we have  ,
,  ,
,  ,
,  . By choosing
. By choosing  and the definition of
and the definition of  and
and  ,
,  ,
,  , one gets
, one gets

Taking  ,
,  and
and  , we have
, we have

that is,  satisfies the conditions (H1)–(H4) of Theorem 5.1. Similarly, we can show that
satisfies the conditions (H1)–(H4) of Theorem 5.1. Similarly, we can show that  satisfies (H1)–(H4). Thus, by Theorem 5.1, the BVP (5.10) has at least three positive solutions
satisfies (H1)–(H4). Thus, by Theorem 5.1, the BVP (5.10) has at least three positive solutions  ,
,  and
and  such that
such that

Remark 5.3.
The particular case  has been studied by [12] for the existence of one solution, our paper generalizes [12] for the obtaining of one and three positive solutions. For
has been studied by [12] for the existence of one solution, our paper generalizes [12] for the obtaining of one and three positive solutions. For  , we develop [13–15] by the nonlinear terms
, we develop [13–15] by the nonlinear terms  involved in the
involved in the  -order Riemann-Liouville derivative explicitly.
-order Riemann-Liouville derivative explicitly.
References
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, New York, NY, USA; 1993:xxxvi+976.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science, Amsterdam, The Netherlands; 2006:xvi+523.
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Vatsala AS: General uniqueness and monotone iterative technique for fractional differential equations. Applied Mathematics Letters 2008,21(8):828-834. 10.1016/j.aml.2007.09.006
El-Sayed AMA, El-Mesiry AEM, El-Saka HAA: On the fractional-order logistic equation. Applied Mathematics Letters 2007,20(7):817-823. 10.1016/j.aml.2006.08.013
El-Sayed AMA, El-Maghrabi EM: Stability of a monotonic solution of a non-autonomous multidimensional delay differential equation of arbitrary (fractional) order. Electronic Journal of Qualitative Theory of Differential Equations 2008, (16):1-9.
Diethelm K, Ford NJ: Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications 2002,265(2):229-248. 10.1006/jmaa.2000.7194
Bai C: Positive solutions for nonlinear fractional differential equations with coefficient that changes sign. Nonlinear Analysis: Theory, Methods & Applications 2006,64(4):677-685. 10.1016/j.na.2005.04.047
Su X: Boundary value problem for a coupled system of nonlinear fractional differential equations. Applied Mathematics Letters 2009,22(1):64-69. 10.1016/j.aml.2008.03.001
Bai Z, Lü H: Positive solutions for boundary value problem of nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2005,311(2):495-505. 10.1016/j.jmaa.2005.02.052
Zhang S: Existence of solution for a boundary value problem of fractional order. Acta Mathematica Scientia 2006,26(2):220-228. 10.1016/S0252-9602(06)60044-1
Zhang S: Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electronic Journal of Differential Equations 2006,2006(36):1-12.
Mawhin J: Topological Degree Methods in Nonlinear Boundary Value Problems, CBMS Regional Conference Series in Mathematics. Volume 40. American Mathematical Society, Providence, RI, USA; 1979:v+122.
Bai Z, Ge W: Existence of three positive solutions for some second-order boundary value problems. Computers & Mathematics with Applications 2004,48(5-6):699-707. 10.1016/j.camwa.2004.03.002
Acknowledgments
This work is supported by National Natural Science Foundation of China (NNSF) (10671012) and the Specialized Research Fund for the Doctoral Program of Higher Education (SRFDP) of China (20050007011).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, A., Ge, W. Positive Solutions for Boundary Value Problems of 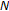 -Dimension Nonlinear Fractional Differential System.
Bound Value Probl 2008, 437453 (2009). https://doi.org/10.1155/2008/437453
-Dimension Nonlinear Fractional Differential System.
Bound Value Probl 2008, 437453 (2009). https://doi.org/10.1155/2008/437453
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/437453