- Research Article
- Open access
- Published:
Global Behavior for a Diffusive Predator-Prey Model with Stage Structure and Nonlinear Density Restriction-I: The Case in 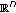
Boundary Value Problems volume 2009, Article number: 378763 (2009)
Abstract
This paper deals with a Holling type III diffusive predator-prey model with stage structure and nonlinear density restriction in the space  . We first consider the asymptotical stability of equilibrium points for the model of ODE type. Then, the existence and uniform boundedness of global solutions and stability of the equilibrium points for the model of weakly coupled reaction-diffusion type are discussed. Finally, the global existence and the convergence of solutions for the model of cross-diffusion type are investigated when the space dimension is less than 6.
. We first consider the asymptotical stability of equilibrium points for the model of ODE type. Then, the existence and uniform boundedness of global solutions and stability of the equilibrium points for the model of weakly coupled reaction-diffusion type are discussed. Finally, the global existence and the convergence of solutions for the model of cross-diffusion type are investigated when the space dimension is less than 6.
1. Introduction
Population models with stage structure have been investigated by many researchers, and various methods and techniques have been used to study the existence and qualitative properties of solutions [1–9]. However, most of the discussions in these works are devoted to either systems of ODE or weakly coupled systems of reaction-diffusion equations. In this paper we investigate the global existence and convergence of solutions for a strongly coupled cross-diffusion predator-prey model with stage structure and nonlinear density restriction. Nonlinear problems of this kind are quite difficult to deal with since the usual idea to apply maximum principle arguments to get priori estimates cannot be used here [10].
Consider the following predator-prey model with stage-structure:

where  ,
,  denote the density of the immature and mature population of the prey, respectively,
denote the density of the immature and mature population of the prey, respectively,  is the density of the predator. For the prey, the immature population is nonlinear density restriction.
is the density of the predator. For the prey, the immature population is nonlinear density restriction.  is assumed to consume
is assumed to consume  with Holling type III functional response
with Holling type III functional response  and contributes to its growth with rate
and contributes to its growth with rate  . For more details on the backgrounds of this model see references [11, 12].
. For more details on the backgrounds of this model see references [11, 12].
Using the scaling  and redenoting
and redenoting  by
by  , we can reduce the system (1.1) to
, we can reduce the system (1.1) to

where 
To take into account the natural tendency of each species to diffuse, we are led to the following PDE system of reaction-diffusion type:

where  is a bounded domain in
is a bounded domain in  with smooth boundary
with smooth boundary  ,
,  is the outward unit normal vector on
is the outward unit normal vector on  , and
, and  .
.  are nonnegative smooth functions on
are nonnegative smooth functions on  . The diffusion coefficients
. The diffusion coefficients  are positive constants. The homogeneous Neumann boundary condition indicates that system (1.3) is self-contained with zero population flux across the boundary. The knowledge for system (1.3) is limited (see [13–17]).
are positive constants. The homogeneous Neumann boundary condition indicates that system (1.3) is self-contained with zero population flux across the boundary. The knowledge for system (1.3) is limited (see [13–17]).
In the recent years there has been considerable interest to investigate the global behavior for models of interacting populations with linear density restriction by taking into account the effect of self-as well as cross-diffusion [18–26]. In this paper we are led to the following cross-diffusion system:

where  are the diffusion rates of the three species, respectively.
are the diffusion rates of the three species, respectively.  are referred as self-diffusion pressures, and
are referred as self-diffusion pressures, and  is cross-diffusion pressure. The term self-diffusion implies the movement of individuals from a higher to a lower concentration region. Cross-diffusion expresses the population fluxes of one species due to the presence of the other species. The value of the cross-diffusion coefficient may be positive, negative, or zero. The term positive cross-diffusion coefficient denotes the movement of the species in the direction of lower concentration of another species and negative cross-diffusion coefficient denotes that one species tends to diffuse in the direction of higher concentration of another species [27]. For
is cross-diffusion pressure. The term self-diffusion implies the movement of individuals from a higher to a lower concentration region. Cross-diffusion expresses the population fluxes of one species due to the presence of the other species. The value of the cross-diffusion coefficient may be positive, negative, or zero. The term positive cross-diffusion coefficient denotes the movement of the species in the direction of lower concentration of another species and negative cross-diffusion coefficient denotes that one species tends to diffuse in the direction of higher concentration of another species [27]. For  , problem (1.4) becomes strongly coupled with a full diffusion matrix. As far as the authors are aware, very few results are known for cross-diffusion systems with stage-structure.
, problem (1.4) becomes strongly coupled with a full diffusion matrix. As far as the authors are aware, very few results are known for cross-diffusion systems with stage-structure.
The main purpose of this paper is to study the asymptotic behavior of the solutions for the reaction-diffusion system (1.3), the global existence, and the convergence of solutions for the cross-diffusion system (1.4). The paper will be organized as follows. In Section 2 a linear stability analysis of equilibrium points for the ODE system (1.2) is given. In Section 3 the uniform bound of the solution and stability of the equilibrium points to the weakly coupled system (1.3) are proved. Section 4 deals with the existence and the convergence of global solutions for the strongly coupled system (1.4).
2. Global Stability for System (1.2)
Let  . If
. If  , then (1.2) has semitrivial equilibria
, then (1.2) has semitrivial equilibria  , where
, where  . To discuss the existence of the positive equilibrium point of (1.2), we give the following assumptions:
. To discuss the existence of the positive equilibrium point of (1.2), we give the following assumptions:

where  . Let one curve
. Let one curve  :
:  , and the other curve
, and the other curve  :
:  . Obviously,
. Obviously,  passes the point
passes the point  . Noting that
. Noting that  attains its maximum at
attains its maximum at  , thus when
, thus when  ,
,  .
.  has the asymptote
has the asymptote  and passes the point
and passes the point  . In this case,
. In this case,  and
and  have unique intersection
have unique intersection  , as shown in Figure 1.
, as shown in Figure 1. is the unique positive equilibrium point of (1.2), where
is the unique positive equilibrium point of (1.2), where  ,
,  ,
,  . In addition, the restriction of the existence of the positive equilibrium can be removed, if
. In addition, the restriction of the existence of the positive equilibrium can be removed, if  .
.

Figure 1
The Jacobian matrix of the equilibrium  is
is

The characteristic equation of  (
( ) is
) is  .
.  is a saddle for
is a saddle for  . In addition, the dimensions of the local unstable and stable manifold of
. In addition, the dimensions of the local unstable and stable manifold of  are 1 and 2, respectively.
are 1 and 2, respectively.  is locally asymptotically stable for
is locally asymptotically stable for  .
.
The Jacobian matrix of the equilibrium  is
is

where  . The characteristic equation of
. The characteristic equation of  (
( ) is
) is  , where
, where

According to Routh-Hurwitz criterion,  is locally asymptotically stable for
is locally asymptotically stable for  and
and  , that is,
, that is,  and
and  .
.
The Jacobian matrix of the equilibrium  is
is

where

The characteristic equation of  (
( ) is
) is  , where
, where

According to Routh-Hurwitz criterion,  is locally asymptotically stable for
is locally asymptotically stable for  . Obviously,
. Obviously,  can be checked by (2.1).
can be checked by (2.1).
Now we discuss the global stability of equilibrium points for (1.2).
Theorem 2.1.
-
(i)
Assume that (2.1),
 (2.8)
(2.8)
hold, then the equilibrium point  of (1.2) is globally asymptotically stable.
of (1.2) is globally asymptotically stable.
-
(ii)
Assume that
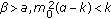 , and
, and 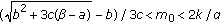 hold, then the equilibrium point
hold, then the equilibrium point 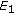 of (1.2) is globally asymptotically stable.
of (1.2) is globally asymptotically stable. -
(iii)
Assume that
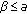 holds, then the equilibrium point
holds, then the equilibrium point 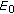 of (1.2) is globally asymptotically stable.
of (1.2) is globally asymptotically stable.
Proof.
-
(i)
Define the Lyapunov function
 (2.9)
(2.9)
Calculating the derivative of  along the positive solution of (1.2), we have
along the positive solution of (1.2), we have

When  , the minimum of
, the minimum of  and
and  is
is  and 0, respectively; the maximum of
and 0, respectively; the maximum of  is
is  are
are  and
and  , respectively. Thus, when (2.8) hold,
, respectively. Thus, when (2.8) hold,  According to the Lyapunov-LaSalle invariance principle [28],
According to the Lyapunov-LaSalle invariance principle [28],  is globally asymptotically stable if (2.1)–(2.3) hold.
is globally asymptotically stable if (2.1)–(2.3) hold.
-
(ii)
Let
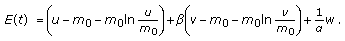 (2.11)
(2.11)
Then

Noting that the maximum of  is
is  , and
, and  , we find
, we find  . Therefore,
. Therefore, 
-
(iii)
Let
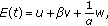 (2.13)
(2.13)
then

Thus,  for
for  . This completes the proof of Theorem 2.1.
. This completes the proof of Theorem 2.1.
3. Global Behavior of System (1.3)
In this section we discuss the existence, uniform boundedness of global solutions, and the stability of constant equilibrium solutions for the weakly coupled reaction-diffusion system (1.3). In particular, the unstability results in Section 2 also hold for system (1.3) because solutions of (1.2) are also solutions of (1.3).
Theorem 3.1.
Let  be nonnegative smooth functions on
be nonnegative smooth functions on  . Then system (1.3) has a unique nonnegative solution
. Then system (1.3) has a unique nonnegative solution  , and
, and

on  . In particular, if
. In particular, if  , then
, then  for all
for all  .
.
Proof.
It is easily seen that  is sufficiently smooth in
is sufficiently smooth in  and possesses a mixed quasimonotone property in
and possesses a mixed quasimonotone property in  . In addition,
. In addition,  and
and  are a pair of lower-upper solutions of problem (1.3) (cf.
are a pair of lower-upper solutions of problem (1.3) (cf.  in (3.1)). From [29, Theorem 5.3.4], we conclude that (1.3) exists a unique classical solution
in (3.1)). From [29, Theorem 5.3.4], we conclude that (1.3) exists a unique classical solution  satisfying (3.1). According to strong maximum principle, it follows that
satisfying (3.1). According to strong maximum principle, it follows that  . So the proof of the Theorem is completed.
. So the proof of the Theorem is completed.
Remark 3.2.
When  (namely
(namely  ), system (1.3) reduces to a system in which the immature population of the prey is linear density restriction. Similar to the proof of Theorem 3.1, we have
), system (1.3) reduces to a system in which the immature population of the prey is linear density restriction. Similar to the proof of Theorem 3.1, we have

Now we show the local and global stability of constant equilibrium solutions  for (1.3), respectively.
for (1.3), respectively.
Theorem 3.3.
-
(i)
Assume that (2.1) holds, then the equilibrium point
 of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable. -
(ii)
Assume that
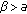 ,
, 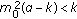 , and
, and 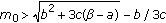 hold, then the equilibrium point
hold, then the equilibrium point  of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable. -
(iii)
Assume that
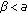 holds, then the equilibrium point
holds, then the equilibrium point 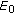 of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable.
Proof.
Let  be the eigenvalues of the operator
be the eigenvalues of the operator  on
on  with Neumann boundary condition, and let
with Neumann boundary condition, and let  be the eigenspace corresponding to
be the eigenspace corresponding to  in
in  . Let
. Let

where  is an orthonormal basis of
is an orthonormal basis of  , then
, then

 Let
Let  ,
,  , where
, where

The linearization of (1.3) is  at
at  . For each
. For each  ,
,  is invariant under the operator L, and
is invariant under the operator L, and  is an eigenvalue of L on
is an eigenvalue of L on  , if and only if
, if and only if  is an eigenvalue of the matrix
is an eigenvalue of the matrix  . The characteristic equation is
. The characteristic equation is  , where
, where

From Routh-Hurwitz criterion, we can see that three eigenvalues (denoted by  ,
,  ,
,  ) all have negative real parts if and only if
) all have negative real parts if and only if  . Noting that
. Noting that  , we must have
, we must have  . It is easy to check that
. It is easy to check that  if
if  (see Section 2).
(see Section 2).
We can conclude that there exists a positive constant  , such that
, such that

In fact, let  , then
, then

Since  as
as  , it follows that
, it follows that

Clearly,  has the three roots
has the three roots  . Let
. Let  . By continuity, there exists
. By continuity, there exists  such that the three roots
such that the three roots  of
of  satisfy
satisfy

Let  , then
, then  . Let
. Let  , then (3.7) holds. According to [30, Theorem 5.1.1], we have the locally asymptotically stability of
, then (3.7) holds. According to [30, Theorem 5.1.1], we have the locally asymptotically stability of  .
.
-
(ii)
The linearization of (1.4) is
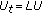 at
at 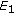 , where
, where 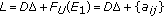 , and
, and 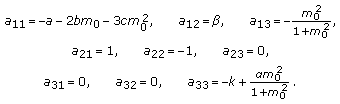 (3.11)
(3.11)
The characteristic equation of  is
is  , where
, where

The three roots of  all have negative real parts for
all have negative real parts for  and
and  . Namely,
. Namely,  is the locally asymptotically stable, if
is the locally asymptotically stable, if  and
and  .
.
-
(iii)
The linearization of (1.3) is
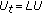 at
at  , where
, where  , and
, and 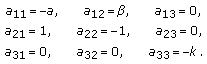 (3.13)
(3.13)
Similar to (i),  is locally asymptotically stable, when
is locally asymptotically stable, when  .
.
Remark 3.4.
When  denote
denote  . If
. If  , then (1.3) has the semitrivial equilibrium point
, then (1.3) has the semitrivial equilibrium point  , where
, where  . If
. If  , then (1.3) has a unique positive equilibrium point
, then (1.3) has a unique positive equilibrium point  . Similar as Theorem 3.3, we have the following.
. Similar as Theorem 3.3, we have the following.
(i)If  ,
,  , and
, and  (namely,
(namely,  ,
,  ,
,  ), then
), then  is locally asymptotically stable.
is locally asymptotically stable.
(ii)If  and
and  , then
, then  is locally asymptotically stable.
is locally asymptotically stable.
(iii)If  , then
, then  is locally asymptotically stable.
is locally asymptotically stable.
Before discussing the global stability, we give an important lemma which has been proved in [31, Lemma  ] or in [32, Lemma
] or in [32, Lemma  ].
].
Lemma 3.5.
Let  be positive constants. Assume that
be positive constants. Assume that  ,
,  , and
, and  is bounded from below. If
is bounded from below. If  and
and  for some positive constant
for some positive constant  , then
, then 
Theorem 3.6.
-
(i)
Assume that (2.1),
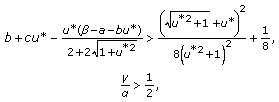 (3.14)
(3.14)
hold, then the equilibrium point  of system (1.3) is globally asymptotically stable.
of system (1.3) is globally asymptotically stable.
-
(ii)
Assume that
 , and
, and  hold, then the equilibrium point
hold, then the equilibrium point 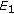 of system (1.3) is globally asymptotically stable.
of system (1.3) is globally asymptotically stable.
(iii)Assume that  and
and  hold, then the equilibrium point
hold, then the equilibrium point  of system (1.3) is globally asymptotically stable.
of system (1.3) is globally asymptotically stable.
Proof.
Let  be the unique positive solution of (1.3). By Theorem 3.1, there exists a positive constant C which is independent of
be the unique positive solution of (1.3). By Theorem 3.1, there exists a positive constant C which is independent of  and
and  such that
such that  , for
, for  . By [33, Theorem
. By [33, Theorem  ],
],

-
(i)
Define the Lyapunov function
 (3.16)
(3.16)
By Theorem 3.1,  is defined well for all solutions of (1.3) with the initial functions
is defined well for all solutions of (1.3) with the initial functions  . It is easily see that
. It is easily see that  and
and  if and only if
if and only if  .
.
Calculating the derivative of  along positive solution of (1.3) by integration by parts and the Cauchy inequality, we have
along positive solution of (1.3) by integration by parts and the Cauchy inequality, we have

It is not hard to verify that

if (3.14) hold. Applying Lemma 3.5, we can obtain

Recomputing  , we find
, we find

From (3.15), we can see that  is bounded in
is bounded in  ,
,  . It follows from Lemma 3.5 and (3.15) that
. It follows from Lemma 3.5 and (3.15) that  as
as  . Namely,
. Namely,

Using the Pioncaré inequality, we have

where  Noting that
Noting that

according to (3.19) and (3.22), we can see

Thus, there exists  as
as  . Applying the boundness of
. Applying the boundness of  , there exists a subsequence of
, there exists a subsequence of  , denoted still by
, denoted still by  , such that
, such that  On the one hand
On the one hand

On the other hand

According to (3.19) to compute the limit of the previous equation and using the uniqueness of the limit, we have  , and
, and

It follows from (3.15) that there exists a subsequence of  , denoted still by
, denoted still by  , and nonnegative functions
, and nonnegative functions  , such that
, such that

Applying (3.19)–(3.27), we obtain that  , and
, and

In view of Theorem 3.3, we can conclude that  is globally asymptotically stable.
is globally asymptotically stable.
-
(ii)
Let
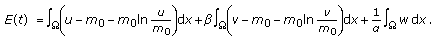 (3.30)
(3.30)
Then

Therefore,  It follows that the equilibrium point
It follows that the equilibrium point  of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable.
-
(iii)
Define
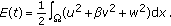 (3.32)
(3.32)
Then

When  ,
,

The following proof is similar to (i).
Remark 3.7.
When  , Theorem 3.6 shows the following.
, Theorem 3.6 shows the following.
-
(i)
Assume that
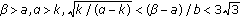 ,
,  (3.35)
(3.35)
hold, then the equilibrium point  of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable.
-
(ii)
Assume that
 hold, then the equilibrium point
hold, then the equilibrium point  of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable. -
(iii)
Assume that
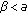 and
and 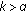 hold, then the equilibrium point
hold, then the equilibrium point 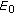 of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable.
Example 3.8.
Consider the following system:

Using the software Matlab, one can obtain  ,
,  . It is easy to see that the previous system satisfies the all conditions of Theorem 3.6(i). So the positive equilibrium point (0.5637,0.5637,0.1199) of the previous system is globally asymptotically stable.
. It is easy to see that the previous system satisfies the all conditions of Theorem 3.6(i). So the positive equilibrium point (0.5637,0.5637,0.1199) of the previous system is globally asymptotically stable.
4. Global Existence and Stability of Solutions for the System (1.4)
By [34–36], we have the following result.
Theorem 4.1.
If  , then (1.4) has a unique nonnegative solution
, then (1.4) has a unique nonnegative solution  , where
, where  is the maximal existence time of the solution. If the solution
is the maximal existence time of the solution. If the solution  satisfies the estimate
satisfies the estimate

then  . If, in addition,
. If, in addition,  , then
, then 
In this section, we consider the existence and the convergence of global solutions to the system (1.4).
Theorem 4.2.
Let  and the space dimension
and the space dimension  . Suppose that
. Suppose that  are nonnegative functions and satisfy zero Neumann boundary conditions. Then (1.4) has a unique nonnegative solution
are nonnegative functions and satisfy zero Neumann boundary conditions. Then (1.4) has a unique nonnegative solution 
In order to prove Theorem 4.2, some preparations are collected firstly.
Lemma 4.3.
Let  be a solution of (1.4). Then
be a solution of (1.4). Then

where  .
.
Proof.
From the maximum principle for parabolic equations, it is not hard to verify that  and
and  is bounded.
is bounded.
Multiplying the second equation of (1.4) by  , adding up the first equation of (1.4), and integrating the result over
, adding up the first equation of (1.4), and integrating the result over  , we obtain
, we obtain

Using Young inequality and H lder inequality, we have
lder inequality, we have

where  It follows from (4.3) and (4.4) that
It follows from (4.3) and (4.4) that

Thus,

where  depends on
depends on  and coefficients of (1.4). In addition, there exists a positive constant
and coefficients of (1.4). In addition, there exists a positive constant  , such that
, such that

Integrating the first equation of (1.4) over  , we have
, we have

Integrating (4.8) from  to
to  , we have
, we have

According to (4.7), there exists a positive constant  , such that
, such that

Multiplying the second equation of (1.4) by  and integrating it over
and integrating it over  , we obtain
, we obtain

Integrating the previous inequation from  to
to  , we have
, we have

Lemma 4.4.
Let  be a solution of (1.4),
be a solution of (1.4),  , and
, and  . Then there exists a positive constant
. Then there exists a positive constant  depending on
depending on  and
and  , such that
, such that

Furthermore  and
and 
Proof.
 satisfies the equation
satisfies the equation

where  are functions of
are functions of  and so are bounded because of Lemma 4.3.
and so are bounded because of Lemma 4.3.
Multiply the second equation of (1.4) by  and integrate it over
and integrate it over  to obtain
to obtain

Then

and  . From a disposal similar to the proof of Lemma 2.2 in [23], we have
. From a disposal similar to the proof of Lemma 2.2 in [23], we have  . Using a standard embedding result, we obtain
. Using a standard embedding result, we obtain 
Lemma 4.5 (see [23, Lemmas 2.3 and 2.4]).
Let  ,
,  , and let
, and let  be any number which may depend on
be any number which may depend on  . Then there is a constant
. Then there is a constant  depending on
depending on  , and
, and  such that
such that

for any  with
with  for all
for all  .
.
To obtain  -estimates of
-estimates of  , we establish
, we establish  -estimates of
-estimates of  in the following lemma.
in the following lemma.
Lemma 4.6.
Let  ,
,  , then there exist positive constants
, then there exist positive constants  and
and  , such that
, such that

Proof.
Multiply the first equation of (1.4) by  for
for  and integrate by parts over
and integrate by parts over  to obtain
to obtain

Integrating (4.19) from 0 to  , we have
, we have

Then substitution of  ,
,  into (4.20) leads to
into (4.20) leads to

It follows from H lder inequality and Lemma 4.3 that
lder inequality and Lemma 4.3 that

Note that  , and
, and  for
for  . From H
. From H lder inequality, Young inequality, and Lemma 4.4, we have
lder inequality, Young inequality, and Lemma 4.4, we have

Substitution of (4.22) and (4.23) into (4.21) leads to

where  is arbitrary and
is arbitrary and  .
.
Choose  such that
such that

then it follows from (4.24) that

Let

Then  for
for

According to Lemma 4.5 and the definition of  , we can see
, we can see

Combining (4.26) and (4.29), we have

where  . Therefore
. Therefore  is bounded from (4.30).
is bounded from (4.30).
From (4.29), we have  . Namely,
. Namely,  ,
,  . Combining (4.28), we have
. Combining (4.28), we have  , where
, where  .
.
Setting  in (4.20) (it is easily checked that
in (4.20) (it is easily checked that  , i.e.,
, i.e.,  ), we have
), we have  .
.
Multiplying the second equation of (1.4) by  and integrating it over
and integrating it over  , we have
, we have

The result of  can be obtained from an analogue of the previous proof of
can be obtained from an analogue of the previous proof of  's.
's.
Lemma 4.7.
Let  , then there exists a positive constant
, then there exists a positive constant  such that
such that

Proof.
We will prove this lemma by [37, Theorem 7.1, page 181]. At first, we rewrite the first two equations of (1.4) as

where  ,
,  ,
,  ,
,  is
is  symbol. It follows from Lemma 4.6 that
symbol. It follows from Lemma 4.6 that  ,
,  .
.
By the third equation of (1.4), we have

It follows from Lemma 4.3 that  is bounded in
is bounded in  . Applying Theorem
. Applying Theorem  [37, Page 204] to (4.34), we have
[37, Page 204] to (4.34), we have

Recall that  satisfy (4.14) in Lemma 4.4, that is,
satisfy (4.14) in Lemma 4.4, that is,

where  is bounded. Since
is bounded. Since  by (4.35), applying Theorem
by (4.35), applying Theorem  [37, page 341-342] to (4.36), we have
[37, page 341-342] to (4.36), we have

It follows from [37, Lemma  , page 80] that
, page 80] that  and so
and so  . Recall from Lemma 4.6 that
. Recall from Lemma 4.6 that  , so that
, so that  by applying Theorem
by applying Theorem  [37, Page 181] to (4.33).
[37, Page 181] to (4.33).
Proof of Theorem 4.2.
Firstly, Theorem 4.2 can be proved in a similar way as Theorem  in [21, 25] when the space dimension
in [21, 25] when the space dimension  .
.
Secondly, for  , applying Lemma
, applying Lemma  [37, Page 80] to (4.36), we have
[37, Page 80] to (4.36), we have

Since  , we obtain
, we obtain

The first two equations can be written in the divergence form as

where  . It follows from Lemmas 4.1, 4.5, and (4.39) that
. It follows from Lemmas 4.1, 4.5, and (4.39) that  are bounded. Thus applying Theorem
are bounded. Thus applying Theorem  [37, Page 204] to (4.40) leads to
[37, Page 204] to (4.40) leads to

We rewrite the third equation of (1.4) as

where  . Applying Schauder estimate [29, Theorem
. Applying Schauder estimate [29, Theorem  , page 114] to (4.42) gives
, page 114] to (4.42) gives

Let

then

where  ,
,  . From (4.41), we have
. From (4.41), we have  . It follows from (4.41) and (4.43) that
. It follows from (4.41) and (4.43) that  . Applying Schauder estimate to (4.45) gives
. Applying Schauder estimate to (4.45) gives

Solving equations (4.44) for  , respectively, we have
, respectively, we have

In particular, to conclude  , we need to repeat the above bootstrap technique. Since
, we need to repeat the above bootstrap technique. Since  is arbitrary, so the classical solution
is arbitrary, so the classical solution  of (1.4) exists globally in time.
of (1.4) exists globally in time.
Now we discuss the global stability of the positive equilibrium  (see Section 2) for (1.4).
(see Section 2) for (1.4).
Theorem 4.8.
Assume that the all conditions in Theorem 4.2, (2.1), and

hold. Let  be the unique positive equilibrium point of (1.4), and let
be the unique positive equilibrium point of (1.4), and let  be a positive solution for (1.4). Then
be a positive solution for (1.4). Then

provided that  is large enough.
is large enough.
Proof.
Define the Lyapunov function

Let  be a positive solution of (1.4), Then
be a positive solution of (1.4), Then

The first integrand in the right hand of the previous inequality is positive definite if

Therefore, when the all conditions in Theorem 4.8 hold, there exists a positive constant  such that
such that

This implies that  . So the proof of Theorem 4.8 is completed.
. So the proof of Theorem 4.8 is completed.
References
Aiello WG, Freedman HI: A time-delay model of single-species growth with stage structure. Mathematical Biosciences 1990, 101(2):139–153. 10.1016/0025-5564(90)90019-U
Zhang X, Chen L, Neumann AU: The stage-structured predator-prey model and optimal harvesting policy. Mathematical Biosciences 2000, 168(2):201–210. 10.1016/S0025-5564(00)00033-X
Liu S, Chen L, Liu Z: Extinction and permanence in nonautonomous competitive system with stage structure. Journal of Mathematical Analysis and Applications 2002, 274(2):667–684. 10.1016/S0022-247X(02)00329-3
Lin Z: Time delayed parabolic system in a two-species competitive model with stage structure. Journal of Mathematical Analysis and Applications 2006, 315(1):202–215. 10.1016/j.jmaa.2005.06.012
Xu R: A reaction-diffusion predator-prey model with stage structure and nonlocal delay. Applied Mathematics and Computation 2006, 175(2):984–1006. 10.1016/j.amc.2005.08.014
Xu R, Chaplain MAJ, Davidson FA: Global convergence of a reaction-diffusion predator-prey model with stage structure for the predator. Applied Mathematics and Computation 2006, 176(1):388–401. 10.1016/j.amc.2005.09.028
Xu R, Chaplain MAJ, Davidson FA: Global convergence of a reaction-diffusion predator-prey model with stage structure and nonlocal delays. Computers & Mathematics with Applications 2007, 53(5):770–788. 10.1016/j.camwa.2007.02.002
Wang M: Stability and Hopf bifurcation for a prey-predator model with prey-stage structure and diffusion. Mathematical Biosciences 2008, 212(2):149–160. 10.1016/j.mbs.2007.08.008
Wang Z, Wu J: Qualitative analysis for a ratio-dependent predator-prey model with stage structure and diffusion. Nonlinear Analysis: Real World Applications 2008, 9(5):2270–2287. 10.1016/j.nonrwa.2007.08.004
Galiano G, Garzón ML, Jüngel A: Semi-discretization in time and numerical convergence of solutions of a nonlinear cross-diffusion population model. Numerische Mathematik 2003, 93(4):655–673. 10.1007/s002110200406
Chen L: Mathematical Models and Methods in Ecology. Science Press, Beijing, China; 1988.
Chen LJ, Sun JH: The uniqueness of a limit cycle for a class of Holling models with functional responses. Acta Mathematica Sinica 2002, 45(2):383–388.
Li W-T, Wu S-L: Traveling waves in a diffusive predator-prey model with Holling type-III functional response. Chaos, Solitons & Fractals 2008, 37(2):476–486. 10.1016/j.chaos.2006.09.039
Ko W, Ryu K: Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge. Journal of Differential Equations 2006, 231(2):534–550. 10.1016/j.jde.2006.08.001
Zhang H, Georgescu P, Chen L: An impulsive predator-prey system with Beddington-DeAngelis functional response and time delay. International Journal of Biomathematics 2008, 1(1):1–17. 10.1142/S1793524508000072
Fan Y, Wang L, Wang M: Notes on multiple bifurcations in a delayed predator-prey model with nonmonotonic functional response. International Journal of Biomathematics 2009, 2(2):129–138. 10.1142/S1793524509000583
Wang F, An Y: Existence of nontrivial solution for a nonlocal elliptic equation with nonlinear boundary condition. Boundary Value Problems 2009, 2009:-8.
Lou Y, Ni W-M: Diffusion, self-diffusion and cross-diffusion. Journal of Differential Equations 1996, 131(1):79–131. 10.1006/jdeq.1996.0157
Lou Y, Ni W-M, Wu Y: On the global existence of a cross-diffusion system. Discrete and Continuous Dynamical Systems 1998, 4(2):193–203.
Shim S-A: Uniform boundedness and convergence of solutions to cross-diffusion systems. Journal of Differential Equations 2002, 185(1):281–305. 10.1006/jdeq.2002.4169
Shim S-A: Uniform boundedness and convergence of solutions to the systems with cross-diffusions dominated by self-diffusions. Nonlinear Analysis: Real World Applications 2003, 4(1):65–86. 10.1016/S1468-1218(02)00014-7
Choi YS, Lui R, Yamada Y: Existence of global solutions for the Shigesada-Kawasaki-Teramoto model with weak cross-diffusion. Discrete and Continuous Dynamical Systems 2003, 9(5):1193–1200.
Choi YS, Lui R, Yamada Y: Existence of global solutions for the Shigesada-Kawasaki-Teramoto model with strongly coupled cross-diffusion. Discrete and Continuous Dynamical Systems 2004, 10(3):719–730.
Pang PYH, Wang MX: Existence of global solutions for a three-species predator-prey model with cross-diffusion. Mathematische Nachrichten 2008, 281(4):555–560. 10.1002/mana.200510624
Fu S, Wen Z, Cui S: Uniform boundedness and stability of global solutions in a strongly coupled three-species cooperating model. Nonlinear Analysis: Real World Applications 2008, 9(2):272–289. 10.1016/j.nonrwa.2006.10.003
Yang F, Fu S: Global solutions for a tritrophic food chain model with diffusion. The Rocky Mountain Journal of Mathematics 2008, 38(5):1785–1812. 10.1216/RMJ-2008-38-5-1785
Dubey B, Das B, Hussain J: A predator-prey interaction model with self and cross-diffusion. Ecological Modelling 2001, 141(1–3):67–76.
Hale JK: Ordinary Differential Equations. Krieger, Malabar, Fla, USA; 1980.
Ye Q, Li Z: Introduction to Reaction-Diffusion Equations. Science Press, Beijing, China; 1999.
Henry D: Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics. Volume 840. Springer, Berlin, Germany; 1993.
Lin Z, Pedersen M: Stability in a diffusive food-chain model with Michaelis-Menten functional response. Nonlinear Analysis: Theory, Methods & Applications 2004, 57(3):421–433. 10.1016/j.na.2004.02.022
Wang M: Nonliear Parabolic Equation of Parabolic Type. Science Press, Beijing, China; 1993.
Brown KJ, Dunne PC, Gardner RA: A semilinear parabolic system arising in the theory of superconductivity. Journal of Differential Equations 1981, 40(2):232–252. 10.1016/0022-0396(81)90020-6
Amann H: Dynamic theory of quasilinear parabolic equations. I. Abstract evolution equations. Nonlinear Analysis: Theory, Methods & Applications 1988, 12(9):895–919. 10.1016/0362-546X(88)90073-9
Amann H: Dynamic theory of quasilinear parabolic equations. II. Reaction-diffusion systems. Differential and Integral Equations 1990, 3(1):13–75.
Amann H: Dynamic theory of quasilinear parabolic systems. III. Global existence. Mathematische Zeitschrift 1989, 202(2):219–250. 10.1007/BF01215256
Ladyženskaja OA, Solonnikov VA, Ural'ceva NN: Linear and Quasilinear Equations of Parabolic Type, Translations of Mathematical Monographs. Volume 23. American Mathematical Society, Providence, RI, USA; 1967:xi+648.
Acknowledgments
This work has been partially supported by the China National Natural Science Foundation (no. 10871160), the NSF of Gansu Province (no. 096RJZA118), the Scientific Research Fund of Gansu Provincial Education Department, and NWNU-KJCXGC-03-47 Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, R., Guo, L. & Fu, S. Global Behavior for a Diffusive Predator-Prey Model with Stage Structure and Nonlinear Density Restriction-I: The Case in  .
Bound Value Probl 2009, 378763 (2009). https://doi.org/10.1155/2009/378763
.
Bound Value Probl 2009, 378763 (2009). https://doi.org/10.1155/2009/378763
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/378763

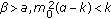 , and
, and 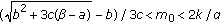 hold, then the equilibrium point
hold, then the equilibrium point 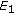 of (1.2) is globally asymptotically stable.
of (1.2) is globally asymptotically stable.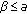 holds, then the equilibrium point
holds, then the equilibrium point 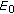 of (1.2) is globally asymptotically stable.
of (1.2) is globally asymptotically stable.
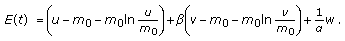
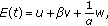
 of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable.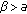 ,
, 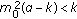 , and
, and 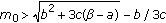 hold, then the equilibrium point
hold, then the equilibrium point  of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable.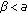 holds, then the equilibrium point
holds, then the equilibrium point 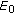 of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable.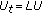 at
at 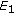 , where
, where 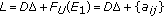 , and
, and 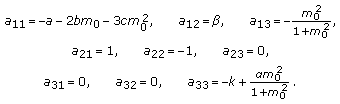
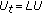 at
at  , where
, where  , and
, and 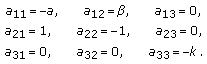
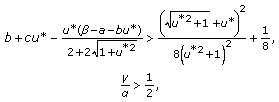
 , and
, and  hold, then the equilibrium point
hold, then the equilibrium point 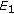 of system (1.3) is globally asymptotically stable.
of system (1.3) is globally asymptotically stable.
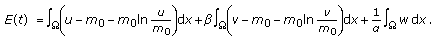
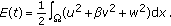
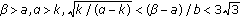 ,
, 
 hold, then the equilibrium point
hold, then the equilibrium point  of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable.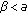 and
and 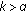 hold, then the equilibrium point
hold, then the equilibrium point 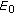 of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable.