- Research Article
- Open access
- Published:
First-Order Singular and Discontinuous Differential Equations
Boundary Value Problems volume 2009, Article number: 507671 (2009)
Abstract
We use subfunctions and superfunctions to derive sufficient conditions for the existence of extremal solutions to initial value problems for ordinary differential equations with discontinuous and singular nonlinearities.
1. Introduction
Let  and
and  be fixed and let
be fixed and let  be a given mapping. We are concerned with the existence of solutions of the initial value problem
be a given mapping. We are concerned with the existence of solutions of the initial value problem

It is well-known that Peano's theorem ensures the existence of local continuously differentiable solutions of (1.1) in case  is continuous. Despite its fundamental importance, it is probably true that Peano's proof of his theorem is even more important than the result itself, which nowadays we know can be deduced quickly from standard fixed point theorems (see [1, Theorem
is continuous. Despite its fundamental importance, it is probably true that Peano's proof of his theorem is even more important than the result itself, which nowadays we know can be deduced quickly from standard fixed point theorems (see [1, Theorem  ] for a proof based on the Schauder's theorem). The reason for believing this is that Peano's original approach to the problem in [2] consisted in obtaining the greatest solution as the pointwise infimum of strict upper solutions. Subsequently this idea was improved by Perron in [3], who also adapted it to study the Laplace equation by means of what we call today Perron's method. For a more recent and important revisitation of the method we mention the work by Goodman [4] on (1.1) in case
] for a proof based on the Schauder's theorem). The reason for believing this is that Peano's original approach to the problem in [2] consisted in obtaining the greatest solution as the pointwise infimum of strict upper solutions. Subsequently this idea was improved by Perron in [3], who also adapted it to study the Laplace equation by means of what we call today Perron's method. For a more recent and important revisitation of the method we mention the work by Goodman [4] on (1.1) in case  is a Carathéodory function. For our purposes in this paper, the importance of Peano's original ideas is that they can be adapted to prove existence results for (1.1) under such weak conditions that standard functional analysis arguments are no longer valid. We refer to differential equations which depend discontinuously on the unknown and several results obtained in papers as [5–9], see also the monographs [10, 11].
is a Carathéodory function. For our purposes in this paper, the importance of Peano's original ideas is that they can be adapted to prove existence results for (1.1) under such weak conditions that standard functional analysis arguments are no longer valid. We refer to differential equations which depend discontinuously on the unknown and several results obtained in papers as [5–9], see also the monographs [10, 11].
On the other hand, singular differential equations have been receiving a lot of attention in the last years, and we can quote [7, 12–19]. The main objective in this paper is to establish an existence result for (1.1) with discontinuous and singular nonlinearities which generalizes in some aspects some of the previously mentioned works.
This paper is organized as follows. In Section 2 we introduce the relevant definitions together with some previously published material which will serve as a basis for proving our main results. In Section 3 we prove the existence of the greatest and the smallest Carathéodory solutions for (1.1) between given lower and upper solutions and assuming the existence of a  -bound for
-bound for  on the sector delimited by the graphs of the lower and upper solutions (regular problems), and we give some examples. In Section 4 we show that looking for piecewise continuous lower and upper solutions is good in practice, but once we have found them we can immediately construct a pair of continuous lower and upper solutions which provide better information on the location of the solutions. In Section 5 we prove two existence results in case
on the sector delimited by the graphs of the lower and upper solutions (regular problems), and we give some examples. In Section 4 we show that looking for piecewise continuous lower and upper solutions is good in practice, but once we have found them we can immediately construct a pair of continuous lower and upper solutions which provide better information on the location of the solutions. In Section 5 we prove two existence results in case  does not have such a strong bound as in Section 3 (singular problems), which requires the addition of some assumptions over the lower and upper solutions. Finally, we prove a result for singular quasimonotone systems in Section 6 and we give some examples in Section 7. Comparison with the literature is provided throughout the paper.
does not have such a strong bound as in Section 3 (singular problems), which requires the addition of some assumptions over the lower and upper solutions. Finally, we prove a result for singular quasimonotone systems in Section 6 and we give some examples in Section 7. Comparison with the literature is provided throughout the paper.
2. Preliminaries
In the following definition  stands for the set of absolutely continuous functions on
stands for the set of absolutely continuous functions on  .
.
Definition 2.1.
A lower solution of (1.1) is a function  such that
such that  and
and  for almost all (a.a.)
for almost all (a.a.)  ; an upper solution is defined analogously reversing the inequalities. One says that
; an upper solution is defined analogously reversing the inequalities. One says that  is a (Carathéodory) solution of (1.1) if it is both a lower and an upper solution. On the other hand, one says that a solution
is a (Carathéodory) solution of (1.1) if it is both a lower and an upper solution. On the other hand, one says that a solution  is the least one if
is the least one if  on
on  for any other solution
for any other solution  , and one defines the greatest solution in a similar way. When both the least and the greatest solutions exist, one calls them the extremal solutions.
, and one defines the greatest solution in a similar way. When both the least and the greatest solutions exist, one calls them the extremal solutions.
It is proven in [8] that (1.1) has extremal solutions if  is
is  -bounded for all
-bounded for all  is measurable, and for a.a.
is measurable, and for a.a.  is quasi-semicontinuous, namely, for all
is quasi-semicontinuous, namely, for all  we have
we have

A similar result was established in [20] assuming moreover that  is superpositionally measurable, and the systems case was considered in [5, 8]. The term "quasi-semicontinuous" in connection with (2.1) was introduced in [5] for the first time and it appears to be conveniently short and descriptive. We note however that, rigorously speaking, we should say that
is superpositionally measurable, and the systems case was considered in [5, 8]. The term "quasi-semicontinuous" in connection with (2.1) was introduced in [5] for the first time and it appears to be conveniently short and descriptive. We note however that, rigorously speaking, we should say that  is left upper and right lower semicontinuous.
is left upper and right lower semicontinuous.
On the other hand, the above assumptions imply that the extremal solutions of (1.1) are given as the infimum of all upper solutions and the supremum of all lower solutions, that is, the least solution of (1.1) is given by

and the greatest solution is

The mappings  and
and  turn out to be the extremal solutions even under more general conditions. It is proven in [9] that solutions exist even if (2.1) fails on the points of a countable family of curves in the conditions of the following definition.
turn out to be the extremal solutions even under more general conditions. It is proven in [9] that solutions exist even if (2.1) fails on the points of a countable family of curves in the conditions of the following definition.
Definition 2.2.
An admissible non-quasi-semicontinuity (nqsc) curve for the differential equation  is the graph of an absolutely continuous function
is the graph of an absolutely continuous function  such that for a.a.
such that for a.a.  one has either
one has either  , or
, or


Remark 2.3.
The condition (2.1) cannot fail over arbitrary curves. As an example note that (1.1) has no solution for  and
and

In this case (2.1) only fails over the line  , but solutions coming from above that line collide with solutions coming from below and there is no way of continuing them to the right once they reach the level
, but solutions coming from above that line collide with solutions coming from below and there is no way of continuing them to the right once they reach the level  . Following Binding [21] we can say that the equation "jams" at
. Following Binding [21] we can say that the equation "jams" at  .
.
An easily applicable sufficient condition for an absolutely continuous function  to be an admissible nqsc curve is that either it is a solution or there exist
to be an admissible nqsc curve is that either it is a solution or there exist  and
and  such that one of the following conditions hold:
such that one of the following conditions hold:
(1) for a.a.
for a.a.  and all
and all  ,
,
(2) for a.a.
for a.a.  and all
and all  .
.
These conditions prevent the differential equation from exhibiting the behavior of the previous example over the line  in several ways. First, if
in several ways. First, if  is a solution of
is a solution of  then any other solution can be continued over
then any other solution can be continued over  once they contact each other and independently of the definition of
once they contact each other and independently of the definition of  around the graph of
around the graph of  . On the other hand, if
. On the other hand, if  holds then solutions of
holds then solutions of  can cross
can cross  from above to below (hence at most once), and if
from above to below (hence at most once), and if  holds then solutions can cross
holds then solutions can cross  from below to above, so in both cases the equation does not jam over the graph of
from below to above, so in both cases the equation does not jam over the graph of  .
.
For the convenience of the reader we state the main results in [9]. The next result establishes the fact that we can have "weak" solutions in a sense just by assuming very general conditions over  .
.
Theorem 2.4.
Suppose that there exists a null-measure set  such that the following conditions hold:
such that the following conditions hold:
(1)condition (2.1) holds for all  except, at most, over a countable family of admissible non-quasi-semicontinuity curves;
except, at most, over a countable family of admissible non-quasi-semicontinuity curves;
(2)there exists an integrable function  ,
,  , such that
, such that

Then the mapping

is absolutely continuous on  and satisfies
and satisfies  and
and  for a.a.
for a.a.  , where
, where  and for all
and for all  the set
the set

contains no positive measure set.
Analogously, the mapping

is absolutely continuous on  and satisfies
and satisfies  and
and  for a.a.
for a.a.  , where
, where  and for all
and for all  the set
the set

contains no positive measure set.
Note that if the sets  and
and  are measurable then
are measurable then  and
and  immediately become the extremal Carathéodory solutions of (1.1). In turn, measurability of those sets can be deduced from some measurability assumptions on
immediately become the extremal Carathéodory solutions of (1.1). In turn, measurability of those sets can be deduced from some measurability assumptions on  . The next lemma is a slight generalization of some results in [8] and the reader can find its proof in [9].
. The next lemma is a slight generalization of some results in [8] and the reader can find its proof in [9].
Lemma 2.5.
Assume that for a null-measure set  the mapping
the mapping  satisfies the following condition.
satisfies the following condition.
For each  ,
,  is measurable, and for
is measurable, and for  one has
one has

Then the mappings  and
and  are measurable for each pair
are measurable for each pair  such that
such that  for all
for all  .
.
Remark 2.6.
A revision of the proof of [9, Lemma  ] shows that it suffices to impose (2.12) for all
] shows that it suffices to impose (2.12) for all  such that
such that  . This fact will be taken into account in this paper.
. This fact will be taken into account in this paper.
As a consequence of Theorem 2.4 and Lemma 2.5 we have a result about existence of extremal Carathéodory solutions for (1.1) and  -bounded nonlinearities. Note that the assumptions in Lemma 2.5 include a restriction over the type of discontinuities that can occur over the admissible nonqsc curves, but remember that such a restriction only plays the role of implying that the sets
-bounded nonlinearities. Note that the assumptions in Lemma 2.5 include a restriction over the type of discontinuities that can occur over the admissible nonqsc curves, but remember that such a restriction only plays the role of implying that the sets  and
and  in Theorem 2.4 are measurable. Therefore, only using the axiom of choice one can find a mapping
in Theorem 2.4 are measurable. Therefore, only using the axiom of choice one can find a mapping  in the conditions of Theorem 2.4 which does not satisfy the assumptions in Lemma 2.5 and for which the corresponding problem (1.1) lacks the greatest (or the least) Carathéodory solution.
in the conditions of Theorem 2.4 which does not satisfy the assumptions in Lemma 2.5 and for which the corresponding problem (1.1) lacks the greatest (or the least) Carathéodory solution.
Theorem 2.7 ([9, Theorem  ]).
]).
Suppose that there exists a null-measure set  such that the following conditions hold:
such that the following conditions hold:
(i)for every  ,
,  is measurable;
is measurable;
(ii)for every  and all
and all  one has either (2.1) or
one has either (2.1) or

and (2.1) can fail, at most, over a countable family of admissible nonquasisemicontinuity curves;
(iii)there exists an integrable function  ,
,  , such that
, such that

Then the mapping  defined in (2.2) is the least Carathéodory solution of (1.1) and the mapping
defined in (2.2) is the least Carathéodory solution of (1.1) and the mapping  defined in (2.3) is the greatest one.
defined in (2.3) is the greatest one.
Remark 2.8.
Theorem  in [9] actually asserts that
in [9] actually asserts that  , as defined in (2.8), is the least Carathéodory solution, but it is easy to prove that in that case
, as defined in (2.8), is the least Carathéodory solution, but it is easy to prove that in that case  , as defined in (2.2). Indeed, let
, as defined in (2.2). Indeed, let  be an arbitrary upper solution of (1.1), let
be an arbitrary upper solution of (1.1), let  and let
and let

Theorem  in [9] implies that also
in [9] implies that also  is the least Carathéodory solution of (1.1), thus
is the least Carathéodory solution of (1.1), thus  on
on  . Hence
. Hence  .
.
Analogously we can prove that  can be replaced by
can be replaced by  in the statement of [21, Theorem
in the statement of [21, Theorem  ].
].
3. Existence between Lower and Upper Solutions
Condition  in Theorem 2.7 is rather restrictive and can be relaxed by assuming boundedness of
in Theorem 2.7 is rather restrictive and can be relaxed by assuming boundedness of  between a lower and an upper solution.
between a lower and an upper solution.
In this section we will prove the following result.
Theorem 3.1.
Suppose that (1.1) has a lower solution  and an upper solution
and an upper solution  such that
such that  for all
for all  and let
and let  .
.
Suppose that there exists a null-measure set  such that the following conditions hold:
such that the following conditions hold:
() for every  , the mapping
, the mapping  with domain
with domain  is measurable;
is measurable;
() for every  ,
,  , one has either (2.1) or (2.13), and (2.1) can fail, at most, over a countable family of admissible non-quasisemicontinuity curves contained in
, one has either (2.1) or (2.13), and (2.1) can fail, at most, over a countable family of admissible non-quasisemicontinuity curves contained in  ;
;
() there exists an integrable function  ,
,  , such that
, such that

Then (1.1) has extremal solutions in the set

Moreover the least solution of (1.1) in  is given by
is given by

and the greatest solution of (1.1) in  is given by
is given by

Proof.
Without loss of generality we suppose that  and
and  exist and satisfy
exist and satisfy  ,
,  ,
,  , and
, and  on
on  . We also may (and we do) assume that every admissible nqsc curve in condition
. We also may (and we do) assume that every admissible nqsc curve in condition  , say
, say  , satisfies for all
, satisfies for all  either
either  or (2.4)-(2.5).
or (2.4)-(2.5).
For each  we define
we define

Claim 1.
The modified problem

satisfies conditions  and
and  in Theorem 2.4 with
in Theorem 2.4 with  replaced by
replaced by  . First we note that
. First we note that  is an immediate consequence of
is an immediate consequence of  and the definition of
and the definition of  .
.
To show that condition  in Theorem 2.4 is satisfied with
in Theorem 2.4 is satisfied with  replaced by
replaced by  , let
, let  be fixed. The verification of (2.1) for
be fixed. The verification of (2.1) for  at
at  is trivial in the following cases:
is trivial in the following cases:  and
and  satisfies (2.1) at
satisfies (2.1) at  ,
,  ,
,  and
and  . Let us consider the remaining situations: we start with the case
. Let us consider the remaining situations: we start with the case  and
and  satisfies (2.1) at
satisfies (2.1) at  , for which we have
, for which we have  and
and

and an analogous argument is valid when  and
and  satisfies (2.1).
satisfies (2.1).
The previous argument shows that  satisfies (2.1) at every
satisfies (2.1) at every  except, at most, over the graphs of the countable family of admissible nonquasisemicontinuity curves in condition
except, at most, over the graphs of the countable family of admissible nonquasisemicontinuity curves in condition  for
for  . Therefore it remains to show that if
. Therefore it remains to show that if  is one of those admissible nqsc curves for
is one of those admissible nqsc curves for  then it is also an admissible nqsc curve for
then it is also an admissible nqsc curve for  . As long as the graph of
. As long as the graph of  remains in the interior of
remains in the interior of  we have nothing to prove because
we have nothing to prove because  and
and  are the same, so let us assume that
are the same, so let us assume that  on a positive measure set
on a positive measure set  ,
,  . Since
. Since  and
and  are absolutely continuous there is a null measure set
are absolutely continuous there is a null measure set  such that
such that  for all
for all  , thus for
, thus for  we have
we have

so condition (2.5) with  replaced by
replaced by  is satisfied on
is satisfied on  . On the other hand, we have to check whether
. On the other hand, we have to check whether  for those
for those  at which we have
at which we have

We distinguish two cases:  and
and  . In the first case (3.9) is equivalent to
. In the first case (3.9) is equivalent to

and therefore either  or condition (2.4) holds, yielding
or condition (2.4) holds, yielding  . If
. If  then we have
then we have  .
.
Analogous arguments show that either  or (2.4)-(2.5) hold for
or (2.4)-(2.5) hold for  at almost every point where
at almost every point where  coincides with
coincides with  , so we conclude that
, so we conclude that  is an admissible nqsc curve for
is an admissible nqsc curve for  .
.
By virtue of Claim 1 and Theorem 2.4 we can ensure that the functions  and
and  defined as
defined as

are absolutely continuous on  and satisfy
and satisfy  and
and  for a.a.
for a.a.  , where
, where  and for all
and for all  the set
the set

contains no positive measure set, and  for a.a.
for a.a.  , where
, where  and for all
and for all  the set
the set

contains no positive measure set.
Claim 2.
For all  we have
we have


Let  be an upper solution of (3.6) and let us show that
be an upper solution of (3.6) and let us show that  for all
for all  . Reasoning by contradiction, assume that there exist
. Reasoning by contradiction, assume that there exist  such that
such that  ,
,  and
and

For a.a.  we have
we have

which together with  imply
imply  on
on  , a contradiction with (3.16). Therefore every upper solution of (3.6) is greater than or equal to
, a contradiction with (3.16). Therefore every upper solution of (3.6) is greater than or equal to  , and, on the other hand,
, and, on the other hand,  is an upper solution of (3.6) with
is an upper solution of (3.6) with  a.e., thus
a.e., thus  satisfies (3.14).
satisfies (3.14).
One can prove by means of analogous arguments that  satisfies (3.15).
satisfies (3.15).
Claim 3.
 is the least solution of (1.1) in
is the least solution of (1.1) in  and
and  is the greatest one. From (3.14) and (3.15) it suffices to show that
is the greatest one. From (3.14) and (3.15) it suffices to show that  and
and  are actually solutions of (3.6). Therefore we only have to prove that
are actually solutions of (3.6). Therefore we only have to prove that  and
and  are null measure sets.
are null measure sets.
Let us show that the set  is a null measure set. First, note that
is a null measure set. First, note that

and we can split  , where
, where  and
and 
Let us show that  is a null measure set. Since
is a null measure set. Since  and
and  are absolutely continuous the set
are absolutely continuous the set

is null. If  then there is some
then there is some  such that
such that  and
and  , but then the definitions of
, but then the definitions of  and
and  yield
yield

Therefore  and thus
and thus  is a null measure set.
is a null measure set.
The set  can be expressed as
can be expressed as  , where for each
, where for each 

For  ,
,  , we have
, we have  , so the definition of
, so the definition of  implies that
implies that

which is a measurable set by virtue of Lemma 2.5 and Remark 2.6.
Since  contains no positive measure subset we can ensure that
contains no positive measure subset we can ensure that  is a null measure set for all
is a null measure set for all  ,
,  , and since
, and since  increases with
increases with  and
and  , we conclude that
, we conclude that  is a null measure set. Finally
is a null measure set. Finally  is null because it is the union of countably many null measure sets.
is null because it is the union of countably many null measure sets.
Analogous arguments show that  is a null measure set, thus the proof of Claim 3 is complete.
is a null measure set, thus the proof of Claim 3 is complete.
Claim 4.
 satisfies (3.3) and
satisfies (3.3) and  satisfies (3.4). Let
satisfies (3.4). Let  be an upper solution of (1.1), let
be an upper solution of (1.1), let  , and for all
, and for all  let
let

Repeating the previous arguments we can prove that also  is the least Carathéodory solution of (1.1) in
is the least Carathéodory solution of (1.1) in  , thus
, thus  on
on  . Hence
. Hence  satisfies (3.3).
satisfies (3.3).
Analogous arguments show that  satisfies (3.4).
satisfies (3.4).
Remark 3.2.
Problem (3.6) may not satisfy condition  in Theorem 2.7 as the compositions
in Theorem 2.7 as the compositions  and
and  need not be measurable. That is why we used Theorem 2.4, instead of Theorem 2.7, to establish Theorem 3.1.
need not be measurable. That is why we used Theorem 2.4, instead of Theorem 2.7, to establish Theorem 3.1.
Next we show that even singular problems may fall inside the scope of Theorem 3.1 if we have adequate pairs of lower and upper solutions.
Example 3.3.
Let us denote by  the integer part of a real number
the integer part of a real number  . We are going to show that the problem
. We are going to show that the problem

has positive solutions. Note that the limit of the right hand side as  tends to the origin does not exist, so the equation is singular at the initial condition.
tends to the origin does not exist, so the equation is singular at the initial condition.
In order to apply Theorem 3.1 we consider (1.1) with  ,
,  , and
, and

It is elementary matter to check that  and
and  ,
,  , are lower and upper solutions for the problem. Condition (2.1) only fails over the graphs of the functions
, are lower and upper solutions for the problem. Condition (2.1) only fails over the graphs of the functions

which are a countable family of admissible nqsc curves at which condition (2.13) holds.
Finally note that

so condition  is satisfied.
is satisfied.
Theorem 3.1 ensures that our problem has extremal solutions between  and
and  which, obviously, are different from zero almost everywhere. Therefore (3.24) has positive solutions.
which, obviously, are different from zero almost everywhere. Therefore (3.24) has positive solutions.
The result of Theorem 3.1 may fail if we assume that condition  is satisfied only in the interior of the set
is satisfied only in the interior of the set  . This is shown in the following example.
. This is shown in the following example.
Example 3.4.
Let us consider problem (1.1) with  ,
,  and
and  defined as
defined as

It is easy to check that  and
and  for all
for all  are lower and upper solutions for this problem and that all the assumptions of Theorem 3.1 are satisfied in the interior of
are lower and upper solutions for this problem and that all the assumptions of Theorem 3.1 are satisfied in the interior of  . However this problem has no solution at all.
. However this problem has no solution at all.
In order to complete the previous information we can say that condition  in the interior of
in the interior of  is enough if we modify the definitions of lower and upper solutions in the following sense.
is enough if we modify the definitions of lower and upper solutions in the following sense.
Theorem 3.5.
Suppose that  and
and  are absolutely continuous functions on
are absolutely continuous functions on  such that
such that  for all
for all  ,
,  ,
,

and let  .
.
Suppose that there exists a null-measure set  such that conditions
such that conditions  and
and  hold and, moreover,
hold and, moreover,
() for every  ,
,  , one has either (2.1) or (2.13), and (2.1) can fail, at most, over a countable family of admissible non-quasisemicontinuity curves contained in
, one has either (2.1) or (2.13), and (2.1) can fail, at most, over a countable family of admissible non-quasisemicontinuity curves contained in  .
.
Then the conclusions of Theorem 3.1 hold true.
Proof (Outline)
It follows the same steps as the proof of Theorem 3.1 but replacing  by
by

Note that condition (2.1) with  replaced by
replaced by  is immediately satisfied over the graphs of
is immediately satisfied over the graphs of  and
and  thanks to the definition of
thanks to the definition of  .
.
Remarks
(i)The function  in Example 3.4 does not satisfy the conditions in Theorem 3.5.
in Example 3.4 does not satisfy the conditions in Theorem 3.5.
-
(ii)
When
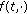 satisfies (2.1) everywhere or almost all
satisfies (2.1) everywhere or almost all 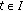 then every couple of lower and upper solutions satisfies the conditions in Theorem 3.5, so this result is not really new in that case (which includes the Carathéodory and continuous cases).
then every couple of lower and upper solutions satisfies the conditions in Theorem 3.5, so this result is not really new in that case (which includes the Carathéodory and continuous cases).
4. Discontinuous Lower and Upper Solutions
Another modification of the concepts of lower and upper solutions concerns the possibility of allowing jumps in their graphs. Since the task of finding a pair of lower and upper solutions is by no means easy in general, and bearing in mind that constant lower and upper solutions are the first reasonable attempt, looking for lower and upper solutions "piece by piece" might make it easier to find them in practical situations. Let us consider the following definition.
Definition 4.1.
One says that  is a piecewise continuous lower solution of (1.1) if there exist
is a piecewise continuous lower solution of (1.1) if there exist  such that
such that
-
(a)
for all
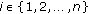 , one has
, one has  and for a.a.
and for a.a. 
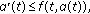 (4.1)
(4.1)
(b) , for all
, for all 

and  .
.
A piecewise continuous upper solution of (1.1) is defined reversing the relevant inequalities.
The existence of a pair of well-ordered piecewise continuous lower and upper solutions implies the existence of a better pair of continuous lower and upper solutions. We establish this more precisely in our next proposition. Note that the proof is constructive.
Proposition 4.2.
Assume that all the conditions in Theorem 3.1 hold with piecewise continuous lower and upper solutions  and
and  .
.
Then the following statements hold:
(i)there exist a lower solution  and an upper solution
and an upper solution  such that
such that

(ii)if  is an upper solution of (1.1) with
is an upper solution of (1.1) with  then
then  , and if
, and if  is a lower solution with
is a lower solution with  then
then  .
.
In particular, the conclusions of Theorem 3.1 remain valid and, moreover, every solution of (1.1) between  and
and  lies between
lies between  and
and  .
.
Proof.
We will only prove the assertions concerning  because the proofs for
because the proofs for  are analogous.
are analogous.
To construct  we simply have to join the points
we simply have to join the points  ,
,  with the graph of
with the graph of  by means of an absolutely continuous curve with derivative less than or equal to
by means of an absolutely continuous curve with derivative less than or equal to  a.e.,
a.e.,  being the function given in
being the function given in  . It can be easily proven that this
. It can be easily proven that this  is a lower solution of (1.1) that lies between
is a lower solution of (1.1) that lies between  and
and  .
.
Moreover, if  is an upper solution of (1.1) between
is an upper solution of (1.1) between  and
and  then we have
then we have

so it cannot go below  .
.
Piecewise continuous lower and upper solutions in the sense of Definition 4.1 were already used in [15, 22]. It is possible to generalize further the concept of lower and upper solutions, as a piecewise continuous lower solution is a particular case of a bounded variation function that has a nonincreasing singular part. Bounded variation lower and upper solutions with monotone singular parts were used in [23, 24], but it is not clear whether Theorem 3.1 is valid with this general type of lower and upper solutions. Anyway, piecewise continuous lower and upper solutions are enough in practical situations, and since these can be transformed into continuous ones which provide better information we will only consider from now on continuous lower and upper solutions as defined in Definition 2.1.
5. Singular Differential Equations
It is the goal of the present section to establish a theorem on existence of solutions for (1.1) between a pair of well-ordered lower and upper solutions and in lack of a local  bound. Solutions will be weak, in the sense of the following definition. By
bound. Solutions will be weak, in the sense of the following definition. By  we denote the set of functions
we denote the set of functions  such that
such that  for all
for all  , and in a similar way we define
, and in a similar way we define  .
.
Definition 5.1.
We say that  is a weak lower solution of (1.1) if
is a weak lower solution of (1.1) if  and
and  for a.a.
for a.a.  . A weak upper solution is defined analogously reversing inequalities. A weak solution of (1.1) is a function which is both a weak lower solution and a weak upper solution.
. A weak upper solution is defined analogously reversing inequalities. A weak solution of (1.1) is a function which is both a weak lower solution and a weak upper solution.
We will also refer to extremal weak solutions with obvious meaning.
Note that (lower/upper) solutions, as defined in Definition 2.1, are weak (lower/upper) solutions but the converse is false in general. For instance the singular linear problem

has exactly the following weak solutions:

and none of them is absolutely continuous on  . Another example, which uses lower and upper solutions, can be found in [15, Remark
. Another example, which uses lower and upper solutions, can be found in [15, Remark  ].
].
However weak (lower/upper) solutions are of Carathéodory type provided they have bounded variation. We establish this fact in the next proposition.
Proposition 5.2.
Let  be such that
be such that  and let
and let  be continuous on
be continuous on  and locally absolutely continuous on
and locally absolutely continuous on  .
.
A necessary and sufficient condition for  to be absolutely continuous on
to be absolutely continuous on  is that
is that  be of bounded variation on
be of bounded variation on  .
.
Proof.
The necessary part is trivial. To estalish the sufficiency of our condition we use Banach-Zarecki's theorem, see [18, Theorem  ]. Let
]. Let  be a null measure set, we have to prove that
be a null measure set, we have to prove that  is also a null measure set. To do this let
is also a null measure set. To do this let  be such that
be such that  . Since
. Since  is absolutely continuous on
is absolutely continuous on  the set
the set  is a null measure set for each
is a null measure set for each  . Therefore
. Therefore  is also a null measure set because
is also a null measure set because

Next we present our main result on existence of weak solutions for (1.1) in absence of integrable bounds.
Theorem 5.3.
Suppose that (1.1) has a weak lower solution  and a weak upper solution
and a weak upper solution  such that
such that  for all
for all  and
and  .
.
Suppose that there is a null-measure set  such that conditions
such that conditions  and
and  in Theorem 3.1 hold for
in Theorem 3.1 hold for  and assume moreover that the following condition holds:
and assume moreover that the following condition holds:
() there exists  such that for all
such that for all  ,
,  , one has
, one has  . Then (1.1) has extremal weak solutions in the set
. Then (1.1) has extremal weak solutions in the set

Moreover the least weak solution of (1.1) in  is given by
is given by

and the greatest weak solution of (1.1) in  is given by
is given by

Proof.
We will only prove that (5.6) defines the greatest weak solution of (1.1) in  , as the arguments to show that (5.5) is the least one are analogous.
, as the arguments to show that (5.5) is the least one are analogous.
First note that  is a weak lower solution between
is a weak lower solution between  and
and  , so
, so  is well defined.
is well defined.
Let  be a decreasing sequence in
be a decreasing sequence in  such that
such that  . Theorem 2.7 ensures that for every
. Theorem 2.7 ensures that for every  the problem
the problem

has extremal Carathéodory solutions between  and
and  . Let
. Let  denote the greatest solution of (5.7) between
denote the greatest solution of (5.7) between  and
and  . By virtue of Theorem 2.7 we also know that
. By virtue of Theorem 2.7 we also know that  is the greatest lower solution of (5.7) between
is the greatest lower solution of (5.7) between  and
and  .
.
Next we prove in several steps that  on
on  for each
for each  .
.
Step 1 ( on
on  for each
for each  ).
).
The restriction to  of each weak lower solution between
of each weak lower solution between  and
and  is a lower solution of (5.7) between
is a lower solution of (5.7) between  and
and  , thus
, thus  is, on the interval
is, on the interval  , greater than or equal to any weak lower solution of (1.1) between
, greater than or equal to any weak lower solution of (1.1) between  and
and  . The definition of
. The definition of  implies then that
implies then that  on
on  .
.
Step 2 ( on
on  for all
for all  ).
).
First, since  on
on  we have
we have  . Reasoning by contradiction, assume that there exists
. Reasoning by contradiction, assume that there exists  such that
such that  . Then there is some
. Then there is some  such that
such that  and
and  on
on  , but then the mapping
, but then the mapping

would be a solution of (5.7) (with  replaced by
replaced by  ) between
) between  and
and  which is greater than
which is greater than  on
on  , a contradiction.
, a contradiction.
The above properties of  imply that the following function is well defined:
imply that the following function is well defined:

Step 3 ( ).
).
Let  be fixed. Condition
be fixed. Condition  implies that for all
implies that for all  such that
such that  we have
we have

with  . Hence for
. Hence for  ,
,  , we have
, we have

and therefore  . Since
. Since  was fixed arbitrarily in the previous arguments, we conclude that
was fixed arbitrarily in the previous arguments, we conclude that  .
.
The continuity of  at
at  follows from the continuity of
follows from the continuity of  and
and  at
at  , the assumption
, the assumption  , and the relation
, and the relation

Step 4 ( is a weak lower solution of (1.1)).
is a weak lower solution of (1.1)).
For  and
and  such that
such that  we have (5.10) with
we have (5.10) with  , hence
, hence  , and for
, and for  ,
,  , Fatou's lemma yields
, Fatou's lemma yields

Hence for a.a.  we have
we have

Let  where
where  and
and  .
.
For  and a.a.
and a.a.  we have
we have  , thus
, thus  for a.a.
for a.a.  .
.
On the other hand, for a.a.  the relation (5.14) and the increasingness of
the relation (5.14) and the increasingness of  yield
yield

Let  be such that (5.15) holds. We have two possibilities: either (2.1) holds for
be such that (5.15) holds. We have two possibilities: either (2.1) holds for  at
at  and then from (5.15) we deduce
and then from (5.15) we deduce  , or
, or  , where
, where  is an admissible curve of non quasisemicontinuity. In the last case we have that either
is an admissible curve of non quasisemicontinuity. In the last case we have that either  belongs to a null-measure set or
belongs to a null-measure set or  , which, in turn, yields two possibilities: either
, which, in turn, yields two possibilities: either  and then
and then  , or
, or  and then (5.15), with
and then (5.15), with  and
and  , and the definition of admissible curve of non quasisemicontinuity imply that
, and the definition of admissible curve of non quasisemicontinuity imply that  .
.
The above arguments prove that  a.e. on
a.e. on  , and since
, and since  was fixed arbitrarily, the proof of Step 4 is complete.
was fixed arbitrarily, the proof of Step 4 is complete.
Conclusion
The construction of  and Step 1 imply that
and Step 1 imply that  and the definition of
and the definition of  and Step 4 imply that
and Step 4 imply that  . Therefore for all
. Therefore for all  we have
we have  on
on  and then
and then  is a weak solution of (1.1). Since every weak solution is a weak lower solution,
is a weak solution of (1.1). Since every weak solution is a weak lower solution,  is the greatest weak solution of (1.1) in
is the greatest weak solution of (1.1) in  .
.
The assumption  in Theorem 5.3 can be replaced by other types of conditions. The next theorem generalizes the main results in [7, 12–14] concerning existence of solutions of singular problems of the type of (1.1).
in Theorem 5.3 can be replaced by other types of conditions. The next theorem generalizes the main results in [7, 12–14] concerning existence of solutions of singular problems of the type of (1.1).
Theorem 5.4.
Suppose that (1.1) with  has a weak lower solution
has a weak lower solution  and a weak upper solution
and a weak upper solution  such that
such that  for all
for all  and
and  on
on  .
.
Suppose that there is a null-measure set  such that conditions
such that conditions  and
and  in Theorem 3.1 hold for
in Theorem 3.1 hold for  and assume moreover that the following condition holds:
and assume moreover that the following condition holds:
() for every  there exists
there exists  such that for all
such that for all  ,
,  , and
, and  one has
one has  .
.
Then the conclusions of Theorem 5.3 hold true.
Proof.
We start observing that there exists a weak upper solution  such that
such that  on
on  and
and  . If
. If  then it suffices to take
then it suffices to take  as
as  . If
. If  we proceed as follows in order to construct
we proceed as follows in order to construct  : let
: let  be a decreasing sequence in
be a decreasing sequence in  such that
such that  and for every
and for every  let
let  be the greatest solution between
be the greatest solution between  and
and  of
of

Claim [ exists]
exists]
Let  be so small that
be so small that  for all
for all  . Condition
. Condition  implies that there exists
implies that there exists  such that for a.a.
such that for a.a.  and all
and all  we have
we have  . Let
. Let  ,
,  and let
and let  be such that
be such that  on
on  . We can apply Theorem 2.7 to the problem
. We can apply Theorem 2.7 to the problem

and with respect to the lower solution  and the upper solution
and the upper solution  , so there exists
, so there exists  the greatest solution between
the greatest solution between  and
and  of (5.17). Notice that if
of (5.17). Notice that if  is a solution of (5.17) then
is a solution of (5.17) then  , so
, so  is also the greatest solution between
is also the greatest solution between  and
and  of (5.17).
of (5.17).
Now condition  ensures that Theorem 2.7 can be applied to the problem
ensures that Theorem 2.7 can be applied to the problem

with respect to the lower solution  and the upper solution
and the upper solution  (both functions restricted to
(both functions restricted to  ). Hence there exists
). Hence there exists  the greatest solution of (5.18) between
the greatest solution of (5.18) between  and
and  .
.
Obviously we have

Analogous arguments to those in the proof of Theorem 5.3 show that  is a weak upper solution and it is clear that
is a weak upper solution and it is clear that  .
.
Finally we show that  holds with
holds with  replaced by
replaced by  . We consider a decreasing sequence
. We consider a decreasing sequence  such that
such that  and
and  . As
. As  and
and  are positive on
are positive on  , we can find
, we can find  such that
such that  on
on  . We deduce then from
. We deduce then from  the existence of
the existence of  so that
so that  for a.e.
for a.e.  and all
and all  . The function
. The function  defined by
defined by  for
for  works.
works.
Theorem 5.3 implies that (1.1) has extremal weak solutions in  which, moreover, satisfy (5.6) and (5.5) with
which, moreover, satisfy (5.6) and (5.5) with  replaced by
replaced by  . Furthermore if
. Furthermore if  is a weak solution of (1.1) in
is a weak solution of (1.1) in  then
then  on
on  . Assume, on the contrary, that
. Assume, on the contrary, that  for some
for some  , then there would exist
, then there would exist  such that
such that  and then
and then  would be a solution of (5.16) between
would be a solution of (5.16) between  and
and  which is strictly greater than
which is strictly greater than  on some subinterval, a contradiction. Hence (1.1) has extremal weak solutions in
on some subinterval, a contradiction. Hence (1.1) has extremal weak solutions in  which, moreover, satisfy (5.6) and (5.5).
which, moreover, satisfy (5.6) and (5.5).
6. Systems
Let us consider the following system of  ordinary differential equations:
ordinary differential equations:

where  ,
,  ,
,  ,
,  , and
, and  .
.
Our goal is to extend Theorem 5.3 to this multidimensional setting, which, as usual, requires the right hand side  to be quasimonotone, as we will define later.
to be quasimonotone, as we will define later.
We start extending to the vector case the definitions given before for scalar problems. To do so, let  denote the set of functions
denote the set of functions  such that for each
such that for each  the component
the component  is absolutely continuous on
is absolutely continuous on  for each
for each  . Also,
. Also,  stands for the class of
stands for the class of  -valued functions which are defined and continuous on
-valued functions which are defined and continuous on  .
.
A weak lower solution of (6.1) is a function  such that for each
such that for each  we have
we have  and for a.a.
and for a.a.  we have
we have  Weak upper solutions are defined similarly by reversing the relevant inequalities, and weak solutions of (6.1) are functions which are both weak lower and weak upper solutions.
Weak upper solutions are defined similarly by reversing the relevant inequalities, and weak solutions of (6.1) are functions which are both weak lower and weak upper solutions.
In the set  we define a partial ordering as follows: let
we define a partial ordering as follows: let  , we write
, we write  if every component of
if every component of  is less than or equal to the corresponding component of
is less than or equal to the corresponding component of  on the whole of
on the whole of  . If
. If  are such that
are such that  then we define
then we define

Extremal (least and greatest) weak solutions of (6.1) in a certain subset of  are defined in the obvious way considering the previous ordering.
are defined in the obvious way considering the previous ordering.
Now we are ready to extend Theorem 5.3 to the vector case. We will denote by  the
the  th canonical vector. The proof follows the line of that of [8, Theorem
th canonical vector. The proof follows the line of that of [8, Theorem  ].
].
Theorem 6.1.
Suppose that (6.1) has weak lower and upper solutions  and
and  such that
such that  ,
,  , and let
, and let  .
.
Suppose that  is quasimonotone nondecreasing in
is quasimonotone nondecreasing in  , that is, for
, that is, for  and
and  the relations
the relations  and
and  imply
imply  .
.
Suppose, moreover, that for each  the following conditions hold:
the following conditions hold:
() the function  is measurable;
is measurable;
() for all  and a.a.
and a.a.  one has either
one has either

or

and (6.3) fails, at most, over a countable family of admissible nqsc curves of the scalar differential equation  contained in the sector
contained in the sector  ;
;
() there exists  such that for
such that for  and a.a.
and a.a.  one has
one has  .
.
Then (6.1) has extremal weak solutions in  . Moreover the least weak solution
. Moreover the least weak solution  is given by
is given by

and the greatest weak solution  is given by
is given by

Proof.
Let  be a weak lower solution of (6.1), and let
be a weak lower solution of (6.1), and let  be as in
be as in  and such that
and such that  a.e. on
a.e. on  for all
for all  . Now let
. Now let  be defined for
be defined for  as
as

In particular,  . Further, every possible solution of (6.1) in
. Further, every possible solution of (6.1) in  is less than or equal to
is less than or equal to  by (6.7) and
by (6.7) and  , independently of
, independently of  .
.
Claim 1 ( ).
).
If  is a weak lower solution in
is a weak lower solution in  with
with  a.e. on
a.e. on  then for
then for  ,
,  , we have
, we have

which implies

and, therefore,  . Further
. Further  is continuous at
is continuous at  because
because  for all
for all  ,
,  and
and  are continuous at
are continuous at  and
and  .
.
Claim 2.
 is the greatest weak solution of (6.1) in
is the greatest weak solution of (6.1) in  . For each weak lower solution
. For each weak lower solution  such that
such that  a.e., the quasimonotonicity of
a.e., the quasimonotonicity of  yields
yields

Hence  is a weak lower solution between
is a weak lower solution between  and
and  of the scalar problem
of the scalar problem

and then Theorem 5.3 implies that  , where
, where  is the greatest weak solution of (6.11) in
is the greatest weak solution of (6.11) in  . Then
. Then  .
.
On the other hand, we have

hence  is a weak lower solution of (6.1) in
is a weak lower solution of (6.1) in  with
with  a.e. on
a.e. on  , thus
, thus  . Therefore
. Therefore  is a weak solution of (6.1), and, by (6.7) and
is a weak solution of (6.1), and, by (6.7) and  , it is the greatest one in
, it is the greatest one in  . In particular, the greatest weak solution of (6.1) in
. In particular, the greatest weak solution of (6.1) in  exists and it is greater than or equal to
exists and it is greater than or equal to  .
.
Claim 3.
The greatest weak solution of (6.1) in  ,
,  , satisfies (6.6). The weak lower solution
, satisfies (6.6). The weak lower solution  was fixed arbitrarily, so
was fixed arbitrarily, so  is greater than or equal to any weak lower solution in
is greater than or equal to any weak lower solution in  . On the other hand,
. On the other hand,  is a weak lower solution.
is a weak lower solution.
Analogously, the least weak solution of (6.1) in  is given by (6.5).
is given by (6.5).
7. Examples
Example 7.1.
Let us show that the following singular and non-quasisemicontinous problem has a unique positive Carathéodory solution:

Here square brackets mean integer part, and by positive solution we mean a solution which is positive on  .
.
First note that (7.1) has at most one positive weak solution because the right hand side in the differential equation is nonincreasing with respect to the unknown on  , thus at no point can solutions bifurcate.
, thus at no point can solutions bifurcate.
For all  we have
we have  and therefore
and therefore  ,
,  , is an upper solution of (7.1) as it solves the majorant problem
, is an upper solution of (7.1) as it solves the majorant problem

On the other hand it is easy to check that for  we have
we have  and then
and then  ,
,  , is a lower solution.
, is a lower solution.
The function  is continuous between the graphs of
is continuous between the graphs of  and
and  except over the lines
except over the lines  ,
,  , which are admissible nqsc curves for all
, which are admissible nqsc curves for all  ,
,  (note that
(note that  is not an admissible nqsc curve but it does not lie between
is not an admissible nqsc curve but it does not lie between  and
and  ).
).
Finally, for  we have
we have

where  is such that
is such that  .
.
Therefore Theorem 5.4 implies the existence of a weak solution of (7.1) between  and
and  . Moreover, this weak solution between
. Moreover, this weak solution between  and
and  is increasing, so Proposition 5.2 ensures that it is, in fact, a Carathéodory solution on
is increasing, so Proposition 5.2 ensures that it is, in fact, a Carathéodory solution on  .
.
It is possible to extend the solution on the right of  to some
to some  where the solution will assume the value
where the solution will assume the value  . The solution cannot be extended further on the right of
. The solution cannot be extended further on the right of  , as (7.1) with
, as (7.1) with  replaced by
replaced by  has no solution on the right of
has no solution on the right of  .
.
We owe to the anonymous referee the following remarks. Problem (7.1) is autonomous, so it falls inside the scope of the results in [21], which ensure that if we find  such that
such that

then (7.1) has a positive absolutely continuous solution defined implicitly by

Since

we deduce that the solution  is defined at least on
is defined at least on  , where
, where  and
and  .
.
Example 7.2.
Let  be measurable and
be measurable and  for a.a.
for a.a.  . We will prove that for each
. We will prove that for each  ,
,  , the problem
, the problem

has a unique positive Carathéodory solution.
Note that the equation is not separable and  assumes positive and negative values on every neighborhood of the initial condition. Moreover the equation is singular at the initial condition with respect to both of its variables.
assumes positive and negative values on every neighborhood of the initial condition. Moreover the equation is singular at the initial condition with respect to both of its variables.
Once again the right hand side in the differential equation is nonincreasing with respect to the unknown  on
on  , thus we have at most one positive weak solution.
, thus we have at most one positive weak solution.
Lower and upper solutions are given by, respectively,  and
and  for
for  .
.
For each  the function
the function  is continuous between the graphs of
is continuous between the graphs of  and
and  except over the lines
except over the lines  ,
,  , where
, where  ,
,  . Let us show that
. Let us show that  is positive between
is positive between  and
and  , thus
, thus  will be an admissible nqsc curve for each
will be an admissible nqsc curve for each  . For
. For  and
and  ,
,  , we have
, we have

and if, moreover, we restrict our attention to those  such that
such that  then we have
then we have  which implies
which implies

and thus for  ,
,  , and
, and  , we have
, we have

This shows that  is positive between
is positive between  and
and  and, moreover, we can say that for
and, moreover, we can say that for  it suffices to take
it suffices to take  such that
such that  to have
to have  for all
for all  between the graphs of
between the graphs of  and
and  and
and  .
.
Therefore Theorem 5.4 implies the existence of a weak solution of (7.7) between  and
and  . Moreover, since
. Moreover, since  is positive between
is positive between  and
and  the solution is increasing and, therefore, it is a Carathéodory solution.
the solution is increasing and, therefore, it is a Carathéodory solution.
The previous two examples fit the conditions of Theorems 5.3 and 5.4. Next we show an example where Theorem 5.3 can be used but it is not clear whether or not we can also apply Theorem 5.4.
Example 7.3.
Let  be fixed and consider the problem
be fixed and consider the problem

Lower and upper solutions are given by  and
and  ,
,  . Since
. Since  is nonnegative between
is nonnegative between  and
and  the lines
the lines  ,
,  , are admissible nqsc curves for the differential equation. Finally it is easy to check that
, are admissible nqsc curves for the differential equation. Finally it is easy to check that  if
if  and
and  , thus one can construct
, thus one can construct  such that
such that  for a.a.
for a.a.  and
and  .
.
Theorem 5.3 ensures that (7.11) has extremal weak solutions between  and
and  . Moreover (7.11) has a unique solution between
. Moreover (7.11) has a unique solution between  and
and  as
as  is nonincreasing with respect to the unknown. Further, the unique solution is monotone and therefore it is a Carathéodory solution.
is nonincreasing with respect to the unknown. Further, the unique solution is monotone and therefore it is a Carathéodory solution.
References
Smart DR: Fixed Point Theorems, Cambridge Tracts in Mathematics, no. 6. Cambridge University Press, London, UK; 1974:viii+93.
Peano G: Sull'integrabilità delle equazioni differenzialli di primo ordine. Atti della Accademia delle Scienze di Torino 1885, 21: 677–685.
Perron O: Ein neuer existenzbeweis für die integrale der differentialgleichung
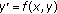 . Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218
. Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218Goodman GS: Subfunctions and intitial-value problem for differential equations satisfying Carathéodory's hypotheses. Journal of Differential Equations 1970, 7: 232–242. 10.1016/0022-0396(70)90108-7
Biles DC, Schechter E: Solvability of a finite or infinite system of discontinuous quasimonotone differential equations. Proceedings of the American Mathematical Society 2000, 128(11):3349–3360. 10.1090/S0002-9939-00-05584-2
Buzzi CA, da Silva PR, Teixeira MA: A singular approach to discontinuous vector fields on the plane. Journal of Differential Equations 2006, 231(2):633–655. 10.1016/j.jde.2006.08.017
Cherpion M, Habets P, López Pouso R: Extremal solutions for first order singular problems with discontinuous nonlinearities. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2003, 10(6):931–947.
Hassan ER, Rzymowski W: Extremal solutions of a discontinuous scalar differential equation. Nonlinear Analysis: Theory, Methods & Applications 1999, 37(8):997–1017. 10.1016/S0362-546X(97)00687-1
López Pouso R: Necessary conditions for solving initial value problems with infima of superfunctions. Mathematical Inequalities & Applications 2005, 8(4):633–641.
Filippov AF: Differential Equations with Discontinuous Righthand Sides, Mathematics and Its Applications (Soviet Series). Volume 18. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1988:x+304.
Heikkilä S, Lakshmikantham V: Monotone Iterative Techniques for Discontinuous Nonlinear Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 181. Marcel Dekker, New York, NY, USA; 1994:xii+514.
Agarwal RP, Franco D, O'Regan D: Singular boundary value problems for first and second order impulsive differential equations. Aequationes Mathematicae 2005, 69(1–2):83–96. 10.1007/s00010-004-2735-9
Agarwal RP, O'Regan D, Lakshmikantham V, Leela S: A generalized upper and lower solution method for singular initial value problems. Computers & Mathematics with Applications 2004, 47(4–5):739–750. 10.1016/S0898-1221(04)90061-2
Agarwal RP, O'Regan D: A survey of recent results for initial and boundary value problems singular in the dependent variable. In Handbook of Differential Equations. Elsevier/North-Holland, Amsterdam, The Netherlands; 2004:1–68.
Cherpion M, De Coster C: Existence of solutions for first order singular problems. Proceedings of the American Mathematical Society 2000, 128(6):1779–1791. 10.1090/S0002-9939-99-05515-X
Chu J, Nieto JJ: Impulsive periodic solutions of first-order singular differential equations. Bulletin of the London Mathematical Society 2008, 40(1):143–150. 10.1112/blms/bdm110
Chu J, Nieto JJ: Recent results for second order singular periodic differential equations. to appear in Boundary Value Problems
Chu J, Torres PJ: Applications of Schauder's fixed point theorem to singular differential equations. Bulletin of the London Mathematical Society 2007, 39(4):653–660. 10.1112/blms/bdm040
O'Regan D: Existence Theory for Nonlinear Ordinary Differential Equations, Mathematics and Its Applications. Volume 398. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:vi+196.
Biles DC, Binding PA: On Carathéodory's conditions for the initial value problem. Proceedings of the American Mathematical Society 1997, 125(5):1371–1376. 10.1090/S0002-9939-97-03942-7
Binding P: The differential equation
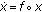 . Journal of Differential Equations 1979, 31(2):183–199. 10.1016/0022-0396(79)90143-8
. Journal of Differential Equations 1979, 31(2):183–199. 10.1016/0022-0396(79)90143-8Liz E, López Pouso R: Upper and lower solutions with "jumps". Journal of Mathematical Analysis and Applications 1998, 222(2):484–493. 10.1006/jmaa.1998.5945
Frigon M, O'Regan D: Existence results for some initial and boundary value problems without growth restriction. Proceedings of the American Mathematical Society 1995, 123(1):207–216. 10.1090/S0002-9939-1995-1233971-2
López Pouso R: Upper and lower solutions for first-order discontinuous ordinary differential equations. Journal of Mathematical Analysis and Applications 2000, 244(2):466–482. 10.1006/jmaa.2000.6717
Hewitt E, Stromberg K: Real and Abstract Analysis. 3rd edition. Springer, New York, NY, USA; 1975:x+476.
Acknowledgments
The research of Rodrigo López Pouso is partially supported by Ministerio de Educación y Ciencia, Spain, Project MTM2007-61724, and by Xunta de Galicia, Spain, Project PGIDIT06PXIB207023PR.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Biles, D., López Pouso, R. First-Order Singular and Discontinuous Differential Equations. Bound Value Probl 2009, 507671 (2009). https://doi.org/10.1155/2009/507671
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/507671
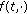 satisfies (2.1) everywhere or almost all
satisfies (2.1) everywhere or almost all 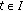 then every couple of lower and upper solutions satisfies the conditions in Theorem 3.5, so this result is not really new in that case (which includes the Carathéodory and continuous cases).
then every couple of lower and upper solutions satisfies the conditions in Theorem 3.5, so this result is not really new in that case (which includes the Carathéodory and continuous cases).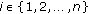 , one has
, one has  and for a.a.
and for a.a. 
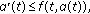
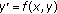 . Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218
. Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218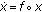 . Journal of Differential Equations 1979, 31(2):183–199. 10.1016/0022-0396(79)90143-8
. Journal of Differential Equations 1979, 31(2):183–199. 10.1016/0022-0396(79)90143-8