- Research Article
- Open access
- Published:
The Existence of Countably Many Positive Solutions for Nonlinear  th-Order Three-Point Boundary Value Problems
th-Order Three-Point Boundary Value Problems
Boundary Value Problems volume 2009, Article number: 572512 (2009)
Abstract
We consider the existence of countably many positive solutions for nonlinear  th-order three-point boundary value problem
th-order three-point boundary value problem  ,
,  ,
,  ,
,  ,
,  , where
, where  ,
,  for some
for some  and has countably many singularities in
and has countably many singularities in  . The associated Green's function for the
. The associated Green's function for the  th-order three-point boundary value problem is first given, and growth conditions are imposed on nonlinearity
th-order three-point boundary value problem is first given, and growth conditions are imposed on nonlinearity  which yield the existence of countably many positive solutions by using the Krasnosel'skii fixed point theorem and Leggett-Williams fixed point theorem for operators on a cone.
which yield the existence of countably many positive solutions by using the Krasnosel'skii fixed point theorem and Leggett-Williams fixed point theorem for operators on a cone.
1. Introduction
The existence of positive solutions for nonlinear second-order and higher-order multipoint boundary value problems has been studied by several authors, for example, see [1–12] and the references therein. However, there are a few papers dealing with the existence of positive solutions for the  th-order multipoint boundary value problems with infinitely many singularities. Hao et al. [13] discussed the existence and multiplicity of positive solutions for the following
th-order multipoint boundary value problems with infinitely many singularities. Hao et al. [13] discussed the existence and multiplicity of positive solutions for the following  th-order nonlinear singular boundary value problems:
th-order nonlinear singular boundary value problems:

where  ,
,  ,
,  may be singular at
may be singular at  and/or
and/or  . Hao et al. established the existence of at least two positive solution for the boundary value problems if
. Hao et al. established the existence of at least two positive solution for the boundary value problems if  is either superlinear or sublinear by applying the Krasnosel'skii-Guo theorem on cone expansion and compression.
is either superlinear or sublinear by applying the Krasnosel'skii-Guo theorem on cone expansion and compression.
In [14], Kaufmann and Kosmatov showed that there exist countably many positive solutions for the two-point boundary value problems with infinitely many singularities of following form:

where  for some
for some  and has countably many singularities in
and has countably many singularities in  .
.
In [15], Ji and Guo proved the existence of countably many positive solutions for the  th-order ordinary differential equation
th-order ordinary differential equation

with one of the following  -point boundary conditions:
-point boundary conditions:

where  ,
,  (
( ),
),  ,
,  (
( ,
, ),
),  ,
, for some
for some  and has countably many singularities in
and has countably many singularities in  .
.
Motivated by the result of [13–15], in this paper we are interested in the existence of countably many positive solutions for nonlinear  th-order three-point boundary value problem
th-order three-point boundary value problem

where  ,
,  ,
,  ,
,  ,
,  ,
,  (
( ,
, ),
),  ,
, for some
for some  and has countably many singularities in
and has countably many singularities in  . We show that the problem (1.5) has countably many solutions if
. We show that the problem (1.5) has countably many solutions if  and
and  satisfy some suitable conditions. Our approach is based on the Krasnosel'skii fixed point theorem and Leggett-Williams fixed point theorem in cones.
satisfy some suitable conditions. Our approach is based on the Krasnosel'skii fixed point theorem and Leggett-Williams fixed point theorem in cones.
Suppose that the following conditions are satisfied.
There exists a sequence  such that
such that  ,
,  ,
,  , and
, and  for all
for all 
There exists  such that
such that  for all
for all  .
.
Assuming that  satisfies the conditions
satisfies the conditions  -
- (we cite [15, Example
(we cite [15, Example  ] to verify existence of
] to verify existence of  ) and imposing growth conditions on the nonlinearity
) and imposing growth conditions on the nonlinearity  , it will be shown that problem (1.5) has infinitely many solutions.
, it will be shown that problem (1.5) has infinitely many solutions.
The paper is organized as follows. In Section 2, we provide some necessary background material such as the Krasnosel'skii fixed-point theorem and Leggett-Williams fixed point theorem in cones. In Section 3, the associated Green's function for the  th-order three-point boundary value problem is first given and we also look at some properties of the Green's function associated with problem (1.5). In Section 4, we prove the existence of countably many positive solutions for problem (1.5) under suitable conditions on
th-order three-point boundary value problem is first given and we also look at some properties of the Green's function associated with problem (1.5). In Section 4, we prove the existence of countably many positive solutions for problem (1.5) under suitable conditions on  and
and  . In Section 5, we give two simple examples to illustrate the applications of obtained results.
. In Section 5, we give two simple examples to illustrate the applications of obtained results.
2. Preliminary Results
Definition 2.1.
Let  be a Banach space over
be a Banach space over  . A nonempty convex closed set
. A nonempty convex closed set  is said to be a cone provided that
is said to be a cone provided that
(i) for all
for all  and for all
and for all  ;
;
(ii) implies
implies  .
.
Definition 2.2.
The map  is said to be a nonnegative continuous concave functional on
is said to be a nonnegative continuous concave functional on  provided that
provided that  is continuous and
is continuous and

for all  and
and  Similarly, we say that the map
Similarly, we say that the map  is a nonnegative continuous convex functional on
is a nonnegative continuous convex functional on  provided that
provided that  is continuous and
is continuous and

for all  and
and 
Definition 2.3.
Let  be given and let
be given and let  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on  . Define the convex sets
. Define the convex sets  and
and  by
by

The following Krasnosel'skii fixed point theorem and Leggett-Williams fixed point theorem play an important role in this paper.
Theorem 2.4 ([16], Krasnosel'skii fixed point theorem).
Let  be a Banach space and let
be a Banach space and let  be a cone. Assume that
be a cone. Assume that  ,
,  are bounded open subsets of
are bounded open subsets of  such that
such that  . Suppose that
. Suppose that

is a completely continuous operator such that, either
(i) , and
, and  , or
, or
(ii) , and
, and  .
.
Then  has a fixed point in
has a fixed point in  .
.
Theorem 2.5 ([17], Leggett-Williams fixed point theorem).
Let  be a completely continuous operator and let
be a completely continuous operator and let  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on  such that
such that  for all
for all  . Suppose there exist
. Suppose there exist  such that
such that
 , and
, and  for
for  ,
,
 for
for  ,
,
 for
for  , with
, with  .
.
Then  has at least three fixed points
has at least three fixed points  , and
, and  such that
such that

In order to establish some of the norm inequalities in Theorems 2.4 and 2.5 we will need Holder's inequality. We use standard notation of  for the space of measurable functions such that
for the space of measurable functions such that

where the integral is understood in the Lebesgue sense. The norm on  , is defined by
, is defined by

Theorem 2.6 ([18], Holder's inequality).
Let  and
and  , where
, where  and
and  . Then
. Then  and, moreover
and, moreover

Let  and
and  . Then
. Then  and
and

3. Preliminary Lemmas
To prove the main results, we need the following lemmas.
Lemma 3.1 (see [15]).
For  the boundary value problem
the boundary value problem

has a unique solution

Lemma 3.2 (see [15]).
The Green's function for the boundary value problem

is given by

Lemma 3.3 (see [15]).
The Green's function  defined by (3.4) satisfies that
defined by (3.4) satisfies that
(i) is continuous on
is continuous on  ;
;
(ii) for all
for all  and there exists a constant
and there exists a constant  for any
for any  such that
such that

where

Lemma 3.4.
Suppose  then for
then for  the boundary value problem
the boundary value problem

has a unique solution

Proof.
The general solution of  can be written as
can be written as

Since  for
for  , we get
, we get  for
for  . Now we solve for
. Now we solve for  by
by  and
and  , it follows that
, it follows that

By solving the above equations, we get

Therefore, (3.7) has a unique solution

Lemma 3.5.
Suppose  , the Green's function for the boundary value problem
, the Green's function for the boundary value problem

is given by

where  is defined by (3.4).
is defined by (3.4).
We omit the proof as it is immediate from Lemma 3.4 and (3.4).
Lemma 3.6.
Suppose  , the Green's function
, the Green's function  defined by (3.14) satisfies that
defined by (3.14) satisfies that
(i) is continuous on
is continuous on  ;
;
(ii) for all
for all  and there exists a constant
and there exists a constant  for any
for any  such that
such that

where

Proof.
 From Lemma 3.3 and (3.14), we get
From Lemma 3.3 and (3.14), we get

 From Lemma 3.3 and (3.14), we have
From Lemma 3.3 and (3.14), we have

Next, we prove that (3.15) holds.
From Lemma 3.3 and (3.14), for  , we have
, we have

for all  , where
, where  ,
,  .
.
We use inequality (3.15) to define our cones. Let  , then
, then  is a Banach space with the norm
is a Banach space with the norm  . For a fixed
. For a fixed  , define the cone
, define the cone  by
by

Define the operator  by
by

Obviously,  is a solution of (1.5) if and only if
is a solution of (1.5) if and only if  is a fixed point of operator
is a fixed point of operator  .
.
Theorems 2.4 and 2.5 require the operator  to be completely continuous and cone preserving. If
to be completely continuous and cone preserving. If  is continuous and compact, then it is completely continuous. The next lemma shows that
is continuous and compact, then it is completely continuous. The next lemma shows that  for
for  and that
and that  is continuous and compact.
is continuous and compact.
Lemma 3.7.
The operator  is completely continuous and
is completely continuous and  for each
for each  .
.
Proof.
Fix  . Since
. Since  for all
for all  ,
,  and since
and since  for all
for all  , then
, then  for all
for all  .
.
Let  , by (3.15) and (3.21) we have
, by (3.15) and (3.21) we have

for all  . Thus
. Thus

Clearly operator (3.21) is continuous. By the Arzela-Ascoli theorem  is compact. Hence, the operator
is compact. Hence, the operator  is completely continuous and the proof is complete.
is completely continuous and the proof is complete.
4. Main Results
In this section we present that problem (1.5) has countably many solutions if  and
and  satisfy some suitable conditions.
satisfy some suitable conditions.
For convenience, we denote

Theorem 4.1.
Suppose conditions  and
and  hold, let
hold, let  be such that
be such that  Let
Let  and
and  be such that
be such that

where  ,
,  . Furthermore, for each natural number
. Furthermore, for each natural number  , assume that
, assume that  satisfies the following two growth conditions:
satisfies the following two growth conditions:
 for all
for all  ,
,
 for all
for all  .
.
Then problem (1.5) has countably many positive solutions  such that
such that  for each
for each 
Proof.
Consider the sequences  and
and  of open subsets of
of open subsets of  defined by
defined by

Let  be as in the hypothesis and note that
be as in the hypothesis and note that  for all
for all  . For each
. For each  , define the cone
, define the cone  by
by

Fixed  and let
and let  . For
. For  , we have
, we have

By condition  , we get
, we get

Now let  , then
, then  for all
for all  . By condition
. By condition  , we get
, we get

It is obvious that  . Therefore, by Theorem 2.4, the operator
. Therefore, by Theorem 2.4, the operator  has at least one fixed point
has at least one fixed point  such that
such that  . Since
. Since  was arbitrary, Theorem 4.1 is completed.
was arbitrary, Theorem 4.1 is completed.
Let  is defined by Theorem 4.1. We define the nonnegative continuous concave functionals
is defined by Theorem 4.1. We define the nonnegative continuous concave functionals  on
on  by
by

We observe here that, for each  ,
,  .
.
For convenience, we denote

Theorem 4.2.
Suppose conditions  and
and  hold, let
hold, let  be such that
be such that  Let
Let  ,
,  , and
, and  be such that
be such that

where  ,
,  . Furthermore, for each natural number
. Furthermore, for each natural number  , assume that
, assume that  satisfies the following growth conditions:
satisfies the following growth conditions:
 for all
for all  ,
,
 for all
for all  ,
,
 for all
for all  .
.
Then problem (1.5) has three infinite families of solutions  , and
, and  such that
such that

for each 
Proof.
We note first that  is completely continuous operator. If
is completely continuous operator. If  , then from properties of
, then from properties of  ,
,  , and by Lemma 3.7,
, and by Lemma 3.7,  . Consequently,
. Consequently,  .
.
If  , then
, then  , and by condition
, and by condition  , we have
, we have

Therefore,  . Standard applications of Arzela-Ascoli theorem imply that
. Standard applications of Arzela-Ascoli theorem imply that  is completely continuous operator.
is completely continuous operator.
In a completely analogous argument, condition  implies that condition
implies that condition  of Theorem 2.5 is satisfied.
of Theorem 2.5 is satisfied.
We now show that condition  of Theorem 2.5 is satisfied. Clearly,
of Theorem 2.5 is satisfied. Clearly,

If  , then
, then  , for
, for  . By condition
. By condition  , we get
, we get

Therefore, condition  of Theorem 2.5 is satisfied.
of Theorem 2.5 is satisfied.
Finally, we show that condition  of Theorem 2.5 is also satisfied.
of Theorem 2.5 is also satisfied.
If  and
and  , then
, then

Therefore, condition  is also satisfied. By Theorem 2.5, There exist three infinite families of solutions
is also satisfied. By Theorem 2.5, There exist three infinite families of solutions  ,
,  , and
, and  for problem (1.5) such that
for problem (1.5) such that

for each  Thus, Theorem 4.2 is completed.
Thus, Theorem 4.2 is completed.
5. Example
In this section, we cite an example (see [15]) to verify existence of  , and two simple examples are presented to illustrate the applications for obtained conclusion of Theorems 4.1 and 4.2.
, and two simple examples are presented to illustrate the applications for obtained conclusion of Theorems 4.1 and 4.2.
Example 5.1.
As an example of problem (1.5), we mention the boundary value problem

where  is defined by [15, Example
is defined by [15, Example  ] and
] and  ,
,

We notice that  ,
,  ,
,  ,
,  .
.
If we take  ,
,  ,
,  ,
,  then
then  , and
, and  =
=  = min
= min ,
,  =
= 
It follows from a direct calculation that

so

In addition, if we take  ,
,  ,
,  ,
,  ,
,  , then
, then

and  satisfies the following growth conditions:
satisfies the following growth conditions:

Then all the conditions of Theorem 4.1 are satisfied. Therefore, by Theorem 4.1 we know that problem (5.1) has countably many positive solutions  such that
such that  for each
for each 
Example 5.2.
As another example of problem (1.5), we mention the boundary value problem

where  is defined by [15, Example
is defined by [15, Example  ] and
] and  ,
,

We notice that  ,
,  ,
,  ,
,  .
.
If we take  =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  then
then  , and
, and  =
=  ,
,  =
=  ,
,  =
= 
It follows from a direct calculation that

In addition, if we take  ,
,  ,
,  ,
,  ,
,  ,
,  , then
, then

and  satisfies the following growth conditions:
satisfies the following growth conditions:

Then all the conditions of Theorem 4.2 are satisfied. Therefore, by Theorem 4.2 we know that problem (5.7) has countably many positive solutions  such that
such that

for each 
Remark 5.3.
In [8–12], the existence of solutions for local or nonlocal boundary value problems of higher-order nonlinear ordinary (fractional) differential equations that has been treated did not discuss problems with singularities. In [13], the singularity only allowed to appear at  and/or
and/or  , the existence and multiplicity of positive solutions were asserted under suitable conditions on
, the existence and multiplicity of positive solutions were asserted under suitable conditions on  . Although, [14, 15] seem to have considered the existence of countably many positive solutions for the second-order and higher-order boundary value problems with infinitely many singularities in
. Although, [14, 15] seem to have considered the existence of countably many positive solutions for the second-order and higher-order boundary value problems with infinitely many singularities in  . However, in [15], only the boundary conditions
. However, in [15], only the boundary conditions  or
or  have been considered. It is clear that the boundary conditions of Examples 5.1 and 5.2 are
have been considered. It is clear that the boundary conditions of Examples 5.1 and 5.2 are  and
and  . Hence, we generalize second-order and higher-order multipoint boundary value problem.
. Hence, we generalize second-order and higher-order multipoint boundary value problem.
References
Il'in VA, Moiseev EI: Nonlocal boundary value problem of the second kind for the Sturm-Liouville operator. Differentsial Equations 1987, 23(8):979–987.
Il'in VA, Moiseev EI: Nonlocal boundary value problem of the first kind for a Sturm-Liouville operator in its differential and finite differenc aspects. Differentsial Equations 1987, 23(7):803–810.
Ma R, Castaneda N: Existence of solutions of nonlinear
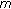 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556–567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556–567. 10.1006/jmaa.2000.7320Ma R: Positive solutions for second-order three-point boundary value problems. Applied Mathematics Letters 2001, 14(1):1–5. 10.1016/S0893-9659(00)00102-6
Liu B: Positive solutions of three-point boundary value problems for the one-dimensional
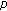 -Laplacian with infinitely many singularities. Applied Mathematics Letters 2004, 17(6):655–661. 10.1016/S0893-9659(04)90100-0
-Laplacian with infinitely many singularities. Applied Mathematics Letters 2004, 17(6):655–661. 10.1016/S0893-9659(04)90100-0Guo Y, Shan W, Ge W: Positive solutions for second-order
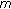 -point boundary value problems. Journal of Computational and Applied Mathematics 2003, 151(2):415–424. 10.1016/S0377-0427(02)00739-2
-point boundary value problems. Journal of Computational and Applied Mathematics 2003, 151(2):415–424. 10.1016/S0377-0427(02)00739-2Guo Y, Ge W: Positive solutions for three-point boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2004, 290(1):291–301. 10.1016/j.jmaa.2003.09.061
Eloe PW, Henderson J: Positive solutions for
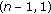 conjugate boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1997, 28(10):1669–1680. 10.1016/0362-546X(95)00238-Q
conjugate boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1997, 28(10):1669–1680. 10.1016/0362-546X(95)00238-QEloe PW, Ahmad B: Positive solutions of a nonlinear
 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009Liu Y, Ge W: Positive solutions for
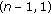 three-point boundary value problems with coefficient that changes sign. Journal of Mathematical Analysis and Applications 2003, 282(2):816–825. 10.1016/S0022-247X(03)00278-6
three-point boundary value problems with coefficient that changes sign. Journal of Mathematical Analysis and Applications 2003, 282(2):816–825. 10.1016/S0022-247X(03)00278-6Guo Y, Ji Y, Zhang J: Three positive solutions for a nonlinear
 th-order
th-order 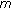 -point boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(11):3485–3492. 10.1016/j.na.2007.03.041
-point boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(11):3485–3492. 10.1016/j.na.2007.03.041Ahmad B, Nieto JJ: Existence of solutions for nonlocal boundary value problems of higher-order nonlinear fractional differential equations. Abstract and Applied Analysis 2009, 2009:-9.
Hao X, Liu L, Wu Y: Positive solutions for nonlinear
 th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.Kaufmann ER, Kosmatov N: A multiplicity result for a boundary value problem with infinitely many singularities. Journal of Mathematical Analysis and Applications 2002, 269(2):444–453. 10.1016/S0022-247X(02)00025-2
Ji Y, Guo Y: The existence of countably many positive solutions for some nonlinear
 th order
th order  -point boundary value problems. Journal of Computational and Applied Mathematics 2009, 232(2):187–200. 10.1016/j.cam.2009.05.023
-point boundary value problems. Journal of Computational and Applied Mathematics 2009, 232(2):187–200. 10.1016/j.cam.2009.05.023Krasnosel'skii MA: Positive Solutions of Operator Equations. Noordhoff, Groningen, The Netherlands; 1964:381.
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana University Mathematics Journal 1979, 28(4):673–688. 10.1512/iumj.1979.28.28046
Beckenbach EF, Bellman R: Inequalities. Springer, Berlin, Germany; 1983:xi+198.
Acknowledgments
The project is supported by the Natural Science Foundation of Hebei Province (A2009000664), the Foundation of Hebei Education Department (2008153), the Foundation of Hebei University of Science and Technology (XL2006040), and the National Natural Science Foundation of PR China (10971045).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ji, Y., Guo, Y. The Existence of Countably Many Positive Solutions for Nonlinear  th-Order Three-Point Boundary Value Problems.
Bound Value Probl 2009, 572512 (2009). https://doi.org/10.1155/2009/572512
th-Order Three-Point Boundary Value Problems.
Bound Value Probl 2009, 572512 (2009). https://doi.org/10.1155/2009/572512
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/572512
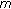 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556–567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556–567. 10.1006/jmaa.2000.7320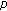 -Laplacian with infinitely many singularities. Applied Mathematics Letters 2004, 17(6):655–661. 10.1016/S0893-9659(04)90100-0
-Laplacian with infinitely many singularities. Applied Mathematics Letters 2004, 17(6):655–661. 10.1016/S0893-9659(04)90100-0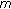 -point boundary value problems. Journal of Computational and Applied Mathematics 2003, 151(2):415–424. 10.1016/S0377-0427(02)00739-2
-point boundary value problems. Journal of Computational and Applied Mathematics 2003, 151(2):415–424. 10.1016/S0377-0427(02)00739-2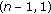 conjugate boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1997, 28(10):1669–1680. 10.1016/0362-546X(95)00238-Q
conjugate boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1997, 28(10):1669–1680. 10.1016/0362-546X(95)00238-Q th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009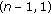 three-point boundary value problems with coefficient that changes sign. Journal of Mathematical Analysis and Applications 2003, 282(2):816–825. 10.1016/S0022-247X(03)00278-6
three-point boundary value problems with coefficient that changes sign. Journal of Mathematical Analysis and Applications 2003, 282(2):816–825. 10.1016/S0022-247X(03)00278-6 th-order
th-order 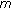 -point boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(11):3485–3492. 10.1016/j.na.2007.03.041
-point boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(11):3485–3492. 10.1016/j.na.2007.03.041 th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10. th order
th order  -point boundary value problems. Journal of Computational and Applied Mathematics 2009, 232(2):187–200. 10.1016/j.cam.2009.05.023
-point boundary value problems. Journal of Computational and Applied Mathematics 2009, 232(2):187–200. 10.1016/j.cam.2009.05.023