- Research Article
- Open access
- Published:
Entire Solutions for a Quasilinear Problem in the Presence of Sublinear and Super-Linear Terms
Boundary Value Problems volume 2009, Article number: 845946 (2009)
Abstract
We establish new results concerning existence and asymptotic behavior of entire, positive, and bounded solutions which converge to zero at infinite for the quasilinear equation 
 where
where  are suitable functions and
are suitable functions and  are not identically zero continuous functions. We show that there exists at least one solution for the above-mentioned problem for each
are not identically zero continuous functions. We show that there exists at least one solution for the above-mentioned problem for each  for some
for some  . Penalty arguments, variational principles, lower-upper solutions, and an approximation procedure will be explored.
. Penalty arguments, variational principles, lower-upper solutions, and an approximation procedure will be explored.
1. Introduction
In this paper we establish new results concerning existence and behavior at infinity of solutions for the nonlinear quasilinear problem

where  , with
, with  , denotes the
, denotes the  -Laplacian operator;
-Laplacian operator;  and
and  are continuous functions not identically zero and
are continuous functions not identically zero and  is a real parameter.
is a real parameter.
A solution of (1.1) is meant as a positive function  with
with  as
as  and
and

The class of problems (1.1) appears in many nonlinear phenomena, for instance, in the theory of quasiregular and quasiconformal mappings [1–3], in the generalized reaction-diffusion theory [4], in the turbulent flow of a gas in porous medium and in the non-Newtonian fluid theory [5]. In the non-Newtonian fluid theory, the quantity  is the characteristic of the medium. If
is the characteristic of the medium. If  , the fluids are called pseudoplastics; if
, the fluids are called pseudoplastics; if  Newtonian and if
Newtonian and if  the fluids are called dilatants.
the fluids are called dilatants.
It follows by the nonnegativity of functions  of parameter
of parameter  and a strong maximum principle that all non-negative and nontrivial solutions of (1.1) must be strictly positive (see Serrin and Zou [6]). So, again of [6], it follows that (1.1) admits one solution if and only if
and a strong maximum principle that all non-negative and nontrivial solutions of (1.1) must be strictly positive (see Serrin and Zou [6]). So, again of [6], it follows that (1.1) admits one solution if and only if  .
.
The main objective of this paper is to improve the principal result of Yang and Xu [7] and to complement other works (see, e.g., [8–20] and references therein) for more general nonlinearities in the terms  and
and  which include the cases considered by them.
which include the cases considered by them.
The principal theorem in [7] considered, in problem (1.1),  and
and  with
with  . Another important fact is that, in our result, we consider different coefficients, while in [7] problem (1.1) was studied with
. Another important fact is that, in our result, we consider different coefficients, while in [7] problem (1.1) was studied with  .
.
In order to establish our results some notations will be introduced. We set

Additionally, we consider
(H1) (i) 
(ii) 
(H2) (i) 
(ii) 
Concerning the coefficients  and
and  ,
,
(H3) (i) 
(ii) 
Our results will be established below under the hypothesis  .
.
Theorem 1.1.
Consider  , then there exists one
, then there exists one  such that for each
such that for each  there exists at least one
there exists at least one  solution of problem (1.1). Moreover,
solution of problem (1.1). Moreover,

for some constant  . If additionally
. If additionally

then there is a positive constant  such that
such that

Remark 1.2.
If we assume (1.5) with  ,
,  , where
, where  , then (1.6) becomes
, then (1.6) becomes

In the sequel, we will establish some results concerning to quasilinear problems which are relevant in itself and will play a key role in the proof of Theorem 1.1.
We begin with the problem of finding classical solutions for the differential inequality

Our result is.
Theorem 1.3.
Consider  , then there exists one
, then there exists one  such that problem (1.8) admits, for each
such that problem (1.8) admits, for each  , at least one radially symmetric solution
, at least one radially symmetric solution  , for some
, for some  . Moreover, if in additionally one assumes (1.5), then there is a positive constant
. Moreover, if in additionally one assumes (1.5), then there is a positive constant  such that
such that

Remark 1.4.
Theorems 1.1 and 1.3 are still true with  if (
if ( ) hypothesis is replaced by
) hypothesis is replaced by

In fact, ( ) implies (
) implies ( )
)  , if
, if  . (see sketch of the proof in the appendix).
. (see sketch of the proof in the appendix).
Remark 1.5.
In Theorem 1.3, it is not necessary to assume that  and
and  are continuous up to
are continuous up to  . It is sufficient to know that
. It is sufficient to know that  are continuous. This includes terms
are continuous. This includes terms  singular in
singular in  .
.
The next result improves one result of Goncalves and Santos [21] because it guarantees the existence of radially symmetric solutions in  for the problem
for the problem

where  ,
,  are continuous and suitable functions and
are continuous and suitable functions and  is the ball in
is the ball in  centered in the origin with radius
centered in the origin with radius  .
.
Theorem 1.6.
Assume  where
where  , with
, with  , is continuous. Suppose that
, is continuous. Suppose that  satisfies (
satisfies ( and additionally
and additionally

then (1.10) admits at least one radially symmetric solution  . Besides this,
. Besides this,  and
and  satisfies
satisfies

The proof of principal theorem (Theorem 1.1) relies mainly on the technics of lower and upper solutions. First, we will prove Theorem 1.3 by defining several auxiliary functions until we get appropriate conditions to define one positive number  and a particular upper solution of (1.1) for each
and a particular upper solution of (1.1) for each  .
.
After this, we will prove Theorem 1.6, motivated by arguments in [21], which will permit us to get a lower solution for (1.1). Finally, we will obtain a solution of (1.1) applying the lemma below due to Yin and Yang [22].
Lemma 1.7.
Suppose that  is defined on
is defined on  and is locally Hölder continuous (with
and is locally Hölder continuous (with  ) in
) in  . Assume also that there exist functions
. Assume also that there exist functions  such that
such that

and  is locally Lipschitz continuous in
is locally Lipschitz continuous in  on the set
on the set

Then there exists  with
with  satisfying
satisfying

In the two next sections we will prove Theorems 1.3 and 1.6.
2. Proof of Theorem (1.4)
First, inspired by Zhang [20] and Santos [16], we will define functions  and
and  by
by

So, for each  , let
, let  given by
given by

where

It is easy to check that

and, as a consequence,

Moreover, it is also easy to verify.
Lemma 2.1.
Suppose that  and
and  hold. Then, for each
hold. Then, for each  ,
,
(i) 
(ii)  ,
,
(iii) 
(iv)  ,
,
(v)  ,
,
(vi) 
By Lemma 2.1(iii), (iv), and (2.2), the function  , given by
, given by

is well defined and continuous. Again, by using Lemma 2.1(i) and (ii),

Besides this,  , for each
, for each  , and using Lemma 2.1, it follows that
, and using Lemma 2.1, it follows that  satisfies, for each
satisfies, for each  , the following.
, the following.
Lemma 2.2.
Suppose that  and
and  hold. Then, for each
hold. Then, for each  ,
,
(i)  ,
,
(ii) 
(iii) 
(iv) 
And, in relation to  , we have the folowing.
, we have the folowing.
Lemma 2.3.
Suppose that  and
and  hold. Then, for each
hold. Then, for each  ,
,
(i)  ,
,
(ii) 
Finally, we will define, for each  ,
,  , by
, by

So,  is a continuous function and we have (see proof in the appendix).
is a continuous function and we have (see proof in the appendix).
Lemma 2.4.
Suppose that  and
and  hold. Then,
hold. Then,
(i) 
(ii) 
(iii) 
(iv) 
(v) 
By Lemma 2.4(ii), there exists a  such that
such that  , where by either (
, where by either ( ) or (
) or ( )
)  , we have
, we have

So, by Lemma 2.4(v), there exists a  such that
such that  . That is,
. That is,

Let  by
by

where  ,
,  is given by
is given by  where
where  is the unique positive and radially symmetric solution of problem
is the unique positive and radially symmetric solution of problem

More specifically, by DiBenedetto [23],  , for some
, for some  . In fact,
. In fact,  satisfies
satisfies

So, by (2.10), (2.11), and (2.13), we have for each  ,
,

Hence, after some pattern calculations, we show that there is a  such that
such that  and
and

As consequences of (2.9), (2.13) and (2.15), we have  and
and

and hence, by Lemma 2.2 (i), (2.7) and  , we obtain
, we obtain

that is, by using (2.2), we have

In particular, making  , we get from (2.15), Lemma 2.2(i) and
, we get from (2.15), Lemma 2.2(i) and  that
that  and satisfies (1.8), for each
and satisfies (1.8), for each  . That is,
. That is,  is an upper solution to (1.1).
is an upper solution to (1.1).
To prove (1.9), first we observe, using Lemma 2.2(i) and (2.15), that

So, by definition of  ,
,  and hypothesis (1.5), we have
and hypothesis (1.5), we have

Thus,

Recalling that  and using (1.5) again, we obtain
and using (1.5) again, we obtain

Thus by (2.9), (2.13), and  , there is one positive constant
, there is one positive constant  such that (1.9) holds. This ends the proof of Theorem 1.3.
such that (1.9) holds. This ends the proof of Theorem 1.3.
3. Proof of Theorem (1.5)
To prove Theorem (1.5), we will first show the existence of a solution, say  , for each
, for each  for the auxiliary problem
for the auxiliary problem

where  In next, to get a solution for problem (1.10), we will use a limit process in
In next, to get a solution for problem (1.10), we will use a limit process in  .
.
For this purpose, we observe that
(i)  ,
,
(ii)  , by (
, by ( ) and by (1.11), it follows that
) and by (1.11), it follows that
(iii)  is non-increasing, for each
is non-increasing, for each 
By items (i)–(iii) above,  and
and  fulfill the assumptions of Theorem 1.3 in [21]. Thus (3.1) admits one solution
fulfill the assumptions of Theorem 1.3 in [21]. Thus (3.1) admits one solution  , for each
, for each  Moreover,
Moreover,  with
with  satisfying
satisfying

Adapting the arguments of the proof of Theorem 1.3 in [21], we show

where  is the positive first eigenfunction of problem
is the positive first eigenfunction of problem

and  , independent of
, independent of  , is chosen (using (
, is chosen (using ( )) such that
)) such that

with  denoting the first eigenvalue of problem (3.4) associated to the
denoting the first eigenvalue of problem (3.4) associated to the  .
.
Hence, by (3.3),

Using ( ), (3.3), the above convergence and Lebesgue's theorem, we have, making
), (3.3), the above convergence and Lebesgue's theorem, we have, making  in (3.2), that
in (3.2), that

So, making  , after some calculations, we obtain that
, after some calculations, we obtain that  . This completes the proof of Theorem 1.6.
. This completes the proof of Theorem 1.6.
4. Proof of Main Result: Theorem 1.1
To complete the proof of Theorem 1.1, we will first obtain a classical and positive lower solution for problem (1.1), say  , such that
, such that  , where
, where  is given by Theorem 1.3. After this, the existence of a solution for the problem (1.1) will be obtained applying Lemma 1.7.
is given by Theorem 1.3. After this, the existence of a solution for the problem (1.1) will be obtained applying Lemma 1.7.
To get a lower solution for (1.1), we will proceed with a limit process in  , where
, where  is a classical solution of problem (1.10) (given by Theorem 1.6) with
is a classical solution of problem (1.10) (given by Theorem 1.6) with  ,
,  is a suitable function and
is a suitable function and  for
for  and
and  is such that
is such that  in
in  .
.
Let

Thus, it is easy to check the following lemma.
Lemma 4.1.
Suppose that  and
and  hold. Then,
hold. Then,
(i) 
(ii)  is non-increasing,
is non-increasing,
(iii)  and
and 
Hence, Lemma 4.1 shows that  fulfills all assumptions of Theorem 1.6. Thus, for each
fulfills all assumptions of Theorem 1.6. Thus, for each  such that
such that  there exists one
there exists one  with
with  and
and  satisfying
satisfying

equivalently,

Consider  extended on
extended on  by
by  . We claim that
. We claim that

Indeed, first we observe that  satisfies Lemma 4.1(ii). So, with similar arguments to those of [21], we show
satisfies Lemma 4.1(ii). So, with similar arguments to those of [21], we show  .
.
To prove  , first we will prove that
, first we will prove that  . In fact, if
. In fact, if  for some
for some  , then there is one
, then there is one  such that
such that

because  and
and  with
with  as
as  .
.
So, using Lemma A.1 (see the appendix) with  , and
, and  , we obtain
, we obtain

and from Lemma 4.1(i),

As a consequence of the contradiction hypothesis and the definition of  , we get
, we get

Recalling that  , it follows that
, it follows that

So,

However, this is impossible. To end the proof of claim (4.4), we will suppose that there exist an  and
and  such that
such that  . Hence, there are
. Hence, there are  with
with  such that
such that  ,
,  and
and  for all
for all  .
.
Following the same above arguments, we obtain

This is impossible again. Thus, we completed the proof of claim (4.4). Setting

it follows by claim (4.4) that

Moreover, making  in (4.3), we use Lebesgue's theorem that
in (4.3), we use Lebesgue's theorem that

Hence, after some calculations, we obtain  and setting
and setting  it follows, by DiBenedetto [23], that
it follows, by DiBenedetto [23], that  for some
for some  . Recalling that
. Recalling that  and using Lemma 4.1(i), it follows that
and using Lemma 4.1(i), it follows that  is a lower solution of (1.1) with
is a lower solution of (1.1) with

So, by Lemma 1.7, we conclude that problem (1.1) admits a solution. Besides this, the inequality (1.4) is a consequence of a result in [6]. This completes the proof of Theorem 1.1.
Appendix
Proof of Lemma 2.4.
The proof of item (iv) is an immediate consequence of Lemma 2.3(i). The item (v) follows by Lemma 2.3(i) and (ii) using Lebesgue's Theorem.
Proof.
By Lemma 2.2(i),

So, using (2.2), (2.5), and Lemma 2.1(i) and (ii), we get

Since, by Lemma 2.1(iv),

then the claim (i) of Lemma 2.4 follows from (A.2).
On the other hand, for all  , it follows from Lemma 2.1(vi) that
, it follows from Lemma 2.1(vi) that

where the last equality is obtained by using ( )-(ii). Hence, using (A.2), the proof of Lemma 2.4(iii) is concluded.
)-(ii). Hence, using (A.2), the proof of Lemma 2.4(iii) is concluded.
Proof.
In this case ( ),
),

That is,  does not depend on
does not depend on  . So, by L'Hopital and Lemma 2.2(iv),
. So, by L'Hopital and Lemma 2.2(iv),

This ends the proof of Lemma 2.4.
The next lemma, proved in [21], was used in the proofs of Theorems 1.1 and 1.6. To enunciate it, we will consider  , for some
, for some  , satisfying
, satisfying

and we define the continuous function  by
by

So, we have  and
and
Lemma A.1.
If  , then
, then

Finally, we will sketch the proof of claim ( ), implies (
), implies ( )
)  , if
, if  .
.
Below,  will denote several positive constants and
will denote several positive constants and  , the function
, the function

If  , by estimating the integral in (A.10), we obtain
, by estimating the integral in (A.10), we obtain

Using the assumption  in the computation of the first integral above and Jensen's inequality to estimate the last one, we have
in the computation of the first integral above and Jensen's inequality to estimate the last one, we have

Computing the above integral, we obtain

Similar calculations show that

So, by ( ),
),

On the other hand, if  , set
, set

and note that either  for all
for all  or
or  for some
for some  . In the first case,
. In the first case,  for all
for all  . Hence
. Hence

So  has a finite limit as
has a finite limit as  , because
, because  . In the second case,
. In the second case,  for
for  and hence,
and hence,

Integrating by parts and estimating using  , we obtain
, we obtain

Again by ( ), we obtain that
), we obtain that  is a finite number. This shows the claim.
is a finite number. This shows the claim.
References
Mikljukov VM: Asymptotic properties of subsolutions of quasilinear equations of elliptic type and mappings with bounded distortion. Matematicheskiĭ Sbornik. Novaya Seriya 1980, 111(1):42-66.
Reshetnyak YuG: Index boundedness condition for mappings with bounded distortion. Siberian Mathematical Journal 1968, 9(2):281-285. 10.1007/BF02204791
Uhlenbeck K: Regularity for a class of non-linear elliptic systems. Acta Mathematica 1977, 138(3-4):219-240.
Herrero MA, Vázquez JL: On the propagation properties of a nonlinear degenerate parabolic equation. Communications in Partial Differential Equations 1982, 7(12):1381-1402. 10.1080/03605308208820255
Esteban JR, Vázquez JL: On the equation of turbulent filtration in one-dimensional porous media. Nonlinear Analysis: Theory, Methods & Applications 1986, 10(11):1303-1325. 10.1016/0362-546X(86)90068-4
Serrin J, Zou H: Cauchy-Liouville and universal boundedness theorems for quasilinear elliptic equations and inequalities. Acta Mathematica 2002, 189(1):79-142. 10.1007/BF02392645
Yang Z, Xu B: Entire bounded solutions for a class of quasilinear elliptic equations. Boundary Value Problems 2007, 2007:-8.
Ambrosetti A, Brezis H, Cerami G: Combined effects of concave and convex nonlinearities in some elliptic problems. Journal of Functional Analysis 1994, 122(2):519-543. 10.1006/jfan.1994.1078
Bartsch T, Willem M: On an elliptic equation with concave and convex nonlinearities. Proceedings of the American Mathematical Society 1995, 123(11):3555-3561. 10.1090/S0002-9939-1995-1301008-2
Brezis H, Kamin S:Sublinear elliptic equations in
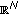 . Manuscripta Mathematica 1992, 74(1):87-106. 10.1007/BF02567660
. Manuscripta Mathematica 1992, 74(1):87-106. 10.1007/BF02567660Brezis H, Oswald L: Remarks on sublinear elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 1986, 10(1):55-64. 10.1016/0362-546X(86)90011-8
Lair AV, Shaker AW: Entire solution of a singular semilinear elliptic problem. Journal of Mathematical Analysis and Applications 1996, 200(2):498-505. 10.1006/jmaa.1996.0218
Lair AV, Shaker AW: Classical and weak solutions of a singular semilinear elliptic problem. Journal of Mathematical Analysis and Applications 1997, 211(2):371-385. 10.1006/jmaa.1997.5470
Goncalves JV, Melo AL, Santos CA:On existence of
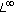 -ground states for singular elliptic equations in the presence of a strongly nonlinear term. Advanced Nonlinear Studies 2007, 7(3):475-490.
-ground states for singular elliptic equations in the presence of a strongly nonlinear term. Advanced Nonlinear Studies 2007, 7(3):475-490.Goncalves JV, Santos CA: Existence and asymptotic behavior of non-radially symmetric ground states of semilinear singular elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2006, 65(4):719-727. 10.1016/j.na.2005.09.036
Santos CA: On ground state solutions for singular and semi-linear problems including super-linear terms at infinity. Nonlinear Analysis: Theory, Methods & Applications. In press
Yang Z: Existence of positive bounded entire solutions for quasilinear elliptic equations. Applied Mathematics and Computation 2004, 156(3):743-754. 10.1016/j.amc.2003.06.024
Ye D, Zhou F: Invariant criteria for existence of bounded positive solutions. Discrete and Continuous Dynamical Systems. Series A 2005, 12(3):413-424.
Zhang Z: A remark on the existence of entire solutions of a singular semilinear elliptic problem. Journal of Mathematical Analysis and Applications 1997, 215(2):579-582. 10.1006/jmaa.1997.5655
Zhang Z: A remark on the existence of positive entire solutions of a sublinear elliptic problem. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(3-4):727-734, 719–727.
Goncalves JV, Santos CAP: Positive solutions for a class of quasilinear singular equations. Electronic Journal of Differential Equations 2004, 56: 1-15.
Yin H, Yang Z: Some new results on the existence of bounded positive entire solutions for quasilinear elliptic equations. Applied Mathematics and Computation 2006, 177(2):606-613. 10.1016/j.amc.2005.09.091
DiBenedetto E:
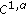 local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 1983, 7(8):827-850. 10.1016/0362-546X(83)90061-5
local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 1983, 7(8):827-850. 10.1016/0362-546X(83)90061-5
Acknowledgment
This research was supported by FEMAT-DF, DPP-UnB.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Santos, C. Entire Solutions for a Quasilinear Problem in the Presence of Sublinear and Super-Linear Terms. Bound Value Probl 2009, 845946 (2009). https://doi.org/10.1155/2009/845946
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/845946
 . Manuscripta Mathematica 1992, 74(1):87-106. 10.1007/BF02567660
. Manuscripta Mathematica 1992, 74(1):87-106. 10.1007/BF02567660 -ground states for singular elliptic equations in the presence of a strongly nonlinear term. Advanced Nonlinear Studies 2007, 7(3):475-490.
-ground states for singular elliptic equations in the presence of a strongly nonlinear term. Advanced Nonlinear Studies 2007, 7(3):475-490. local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 1983, 7(8):827-850. 10.1016/0362-546X(83)90061-5
local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 1983, 7(8):827-850. 10.1016/0362-546X(83)90061-5