- Research Article
- Open access
- Published:
Multiple Solutions for Biharmonic Equations with Asymptotically Linear Nonlinearities
Boundary Value Problems volume 2010, Article number: 241518 (2010)
Abstract
The existence of multiple solutions for a class of fourth elliptic equation with respect to the resonance and nonresonance conditions is established by using the minimax method and Morse theory.
1. Introduction
Consider the following Navier boundary value problem:

where  is a bounded smooth domain in
is a bounded smooth domain in  , and
, and  satisfies the following:
satisfies the following:
 for all
for all  ,
, 
 uniformly for
uniformly for  , where
, where  and
and  are constants;
are constants;
 , where
, where 
In view of the condition  , problem (1.1) is called asymptotically linear at both zero and infinity. Clearly,
, problem (1.1) is called asymptotically linear at both zero and infinity. Clearly,  is a trivial solution of problem (1.1). It follows from
is a trivial solution of problem (1.1). It follows from  and
and  that the functional
that the functional

is of  on the space
on the space  with the norm
with the norm

Under the condition  , the critical points of
, the critical points of  are solutions of problem (1.1). Let
are solutions of problem (1.1). Let  be the eigenvalues of
be the eigenvalues of  and
and  be the eigenfunction corresponding to
be the eigenfunction corresponding to  . Let
. Let  denote the eigenspace associated to
denote the eigenspace associated to  . Throughout this paper, we denoted by
. Throughout this paper, we denoted by  the
the  norm.
norm.
If  in the above condition
in the above condition  is an eigenvalue of
is an eigenvalue of  then problem (1.1) is called resonance at infinity. Otherwise, we call it non-resonance. A main tool of seeking the critical points of functional
then problem (1.1) is called resonance at infinity. Otherwise, we call it non-resonance. A main tool of seeking the critical points of functional  is the mountain pass theorem (see [1–3]). To apply this theorem to the functional
is the mountain pass theorem (see [1–3]). To apply this theorem to the functional  in (1.2), usually we need the following condition [1], that is, for some
in (1.2), usually we need the following condition [1], that is, for some  and
and  ,
,
(AR)

It is well known that the condition (AR) plays an important role in verifying that the functional  has a "mountain pass" geometry and a related
has a "mountain pass" geometry and a related  sequence is bounded in
sequence is bounded in  when one uses the mountain pass theorem.
when one uses the mountain pass theorem.
If  admits subcritical growth and satisfies (AR) condition by the standard argument of applying mountain pass theorem, we known that problem (1.1) has nontrivial solutions. Similarly, lase
admits subcritical growth and satisfies (AR) condition by the standard argument of applying mountain pass theorem, we known that problem (1.1) has nontrivial solutions. Similarly, lase  is of critical growth (see, e.g., [4–7] and their references).
is of critical growth (see, e.g., [4–7] and their references).
It follows from the condition (AR) that  after a simple computation. That is,
after a simple computation. That is,  must be superlinear with respect to
must be superlinear with respect to  at infinity. Noticing our condition
at infinity. Noticing our condition  the nonlinear term
the nonlinear term  is asymptotically linear, not superlinear, with respect to
is asymptotically linear, not superlinear, with respect to  at infinity, which means that the usual condition (AR) cannot be assumed in our case. If the mountain pass theorem is used to seek the critical points of
at infinity, which means that the usual condition (AR) cannot be assumed in our case. If the mountain pass theorem is used to seek the critical points of  , it is difficult to verify that the functional
, it is difficult to verify that the functional  has a "mountain pass" structure and the
has a "mountain pass" structure and the  sequence is bounded.
sequence is bounded.
In [8], Zhou studied the following elliptic problem:

where the conditions on  are similar to
are similar to  and
and  He provided a valid method to verify the
He provided a valid method to verify the  sequence of the variational functional, for the above problem is bounded in
sequence of the variational functional, for the above problem is bounded in  (see also [9, 10]).
(see also [9, 10]).
To the author's knowledge, there seems few results on problem (1.1) when  is asymptotically linear at infinity. However, the method in [8] cannot be applied directly to the biharmonic problems. For example, for the Laplacian problem,
is asymptotically linear at infinity. However, the method in [8] cannot be applied directly to the biharmonic problems. For example, for the Laplacian problem,  implies
implies  where
where  We can use
We can use  or
or  as a test function, which is helpful in proving a solution nonnegative. While for the biharmonic problems, this trick fails completely since
as a test function, which is helpful in proving a solution nonnegative. While for the biharmonic problems, this trick fails completely since  does not imply
does not imply  (see [11, Remark
(see [11, Remark  ]). As far as this point is concerned, we will make use of the methods in [12] to discuss in the following Lemma 2.3. In this paper we consider multiple solutions of problem (1.1) in the cases of resonance and non-resonance by using the mountain pass theorem and Morse theory. At first, we use the truncated skill and mountain pass theorem to obtain a positive solution and a negative solution of problem (1.1) under our more general condition
]). As far as this point is concerned, we will make use of the methods in [12] to discuss in the following Lemma 2.3. In this paper we consider multiple solutions of problem (1.1) in the cases of resonance and non-resonance by using the mountain pass theorem and Morse theory. At first, we use the truncated skill and mountain pass theorem to obtain a positive solution and a negative solution of problem (1.1) under our more general condition  and
and  with respect to the conditions
with respect to the conditions  and
and  in [8]. In the course of proving existence of positive solution and negative solution, the monotonicity condition
in [8]. In the course of proving existence of positive solution and negative solution, the monotonicity condition  of [8] on the nonlinear term
of [8] on the nonlinear term  is not necessary, this point is very important because we can directly prove existence of positive solution and negative solution by using Rabinowitz's mountain pass theorem. That is, the proof of our compact condition is more simple than that in [8]. Furthermore, we can obtain a nontrivial solution when the nonlinear term
is not necessary, this point is very important because we can directly prove existence of positive solution and negative solution by using Rabinowitz's mountain pass theorem. That is, the proof of our compact condition is more simple than that in [8]. Furthermore, we can obtain a nontrivial solution when the nonlinear term  is resonance or non-resonance at the infinity by using Morse theory.
is resonance or non-resonance at the infinity by using Morse theory.
2. Main Results and Auxiliary Lemmas
Let us now state the main results.
Theorem 2.1.
Assume that conditions  and
and  hold,
hold,  , and
, and  for some
for some  ; then problem (1.1) has at least three nontrivial solutions.
; then problem (1.1) has at least three nontrivial solutions.
Theorem 2.2.
Assume that conditions  )–(
)–( hold,
hold,  and
and  for some
for some  ; then problem (1.1) has at least three nontrivial solutions.
; then problem (1.1) has at least three nontrivial solutions.
Consider the following problem:

where

Define a functional  by
by

where  and then
and then 
Lemma 2.3.
 satisfies the (PS) condition.
satisfies the (PS) condition.
Proof.
Let  be a sequence such that
be a sequence such that 
 as
as  Note that
Note that

for all  Assume that
Assume that  is bounded, taking
is bounded, taking  in (2.4). By
in (2.4). By  , there exists
, there exists  such that
such that  a.e.
a.e.  So
So  is bounded in
is bounded in  . If
. If  as
as  set
set  , and then
, and then  . Taking
. Taking  in (2.4), it follows that
in (2.4), it follows that  is bounded. Without loss of generality, we assume that
is bounded. Without loss of generality, we assume that  in
in  , and then
, and then  in
in  . Hence,
. Hence,  a.e. in
a.e. in  . Dividing both sides of (2.4) by
. Dividing both sides of (2.4) by  , we get
, we get

Then for a.e.  , we deduce that
, we deduce that  as
as  where
where  . In fact, when
. In fact, when  by
by  we have
we have

When  , we have
, we have

When  , we have
, we have

Since  , by (2.5) and the Lebesgue dominated convergence theorem, we arrive at
, by (2.5) and the Lebesgue dominated convergence theorem, we arrive at

Choosing  , we deduce that
, we deduce that

Notice that

where 
Now we show that there is a contradiction in both cases of  and
and 
Case 1.
Suppose  then
then  a.e. in
a.e. in  By
By  we have
we have  Thus (2.11) implies that
Thus (2.11) implies that

which contradicts to 
Case 2.
Suppose  then
then  and
and  It follows from (2.11) that
It follows from (2.11) that

which contradicts to  if
if  and contradicts to
and contradicts to  if
if 
Lemma 2.4.
Let  be the eigenfunction corresponding to
be the eigenfunction corresponding to  with
with  . If
. If  , then
, then
(a) there exist  such that
such that  for all
for all  with
with  ;
;
(b)  as
as  .
.
Proof.
By  and
and  , if
, if  , for any
, for any  , there exist
, there exist  and
and  such that for all
such that for all  ,
,


where  if
if 
Choose  such that
such that  By (2.14), the Poincaré inequality, and the Sobolev inequality, we get
By (2.14), the Poincaré inequality, and the Sobolev inequality, we get

So, part (a) holds if we choose  small enough.
small enough.
On the other hand, if  take
take  such that
such that  . By (2.15), we have
. By (2.15), we have

Since  and
and  , it is easy to see that
, it is easy to see that

and part (b) is proved.
Lemma 2.5.
Let  , where
, where  . If
. If  satisfies
satisfies  )–(
)–( then
then
(i) the functional  is coercive on
is coercive on  , that is,
, that is,

and bounded from below on  ;
;
(ii) the functional  is anticoercive on
is anticoercive on  .
.
Proof.
For  , by
, by  , for any
, for any  , there exists
, there exists  such that for all
such that for all  ,
,

So we have

Choose  such that
such that  This proves (i).
This proves (i).
-
(ii)
We firstly consider the case
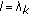 . Write
. Write 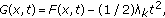
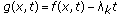 . Then
. Then 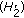 and
and 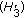 imply that
imply that 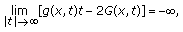 (2.22)
(2.22)

It follows from (2.22) that for every  , there exists a constant
, there exists a constant  such that
such that

For  we have
we have

Integrating (2.25) over  , we deduce that
, we deduce that

Let  and use (2.23); we see that
and use (2.23); we see that  for
for  a.e.
a.e.  A similar argument shows that
A similar argument shows that  for
for  a.e.
a.e.  . Hence
. Hence

By (2.27), we get

for  with
with  , where
, where 
In the case of  , we do not need the assumption
, we do not need the assumption  and it is easy to see that the conclusion also holds.
and it is easy to see that the conclusion also holds.
Lemma 2.6.
If  , then
, then  satisfies the (PS) condition.
satisfies the (PS) condition.
Proof.
Let  be a sequence such that
be a sequence such that 
 . One has
. One has

for all  If
If  is bounded, we can take
is bounded, we can take  . By
. By  , there exists a constant
, there exists a constant  such that
such that  a.e.
a.e.  So
So  is bounded in
is bounded in  . If
. If  , as
, as  set
set  , and then
, and then  . Taking
. Taking  in (2.29), it follows that
in (2.29), it follows that  is bounded. Without loss of generality, we assume
is bounded. Without loss of generality, we assume  in
in  , and then
, and then  in
in  . Hence,
. Hence,  a.e. in
a.e. in  . Dividing both sides of (2.29) by
. Dividing both sides of (2.29) by  , we get
, we get

Then for a.e.  , we have
, we have  as
as  In fact, if
In fact, if  by
by  , we have
, we have

If  , we have
, we have

Since  , by (2.30) and the Lebesgue dominated convergence theorem, we arrive at
, by (2.30) and the Lebesgue dominated convergence theorem, we arrive at

It is easy to see that  . In fact, if
. In fact, if  , then
, then  contradicts to
contradicts to  . Hence,
. Hence,  is an eigenvalue of
is an eigenvalue of  . This contradicts our assumption.
. This contradicts our assumption.
Lemma 2.7.
Suppose that  and
and  satisfies
satisfies  . Then the functional
. Then the functional  satisfies the (C) condition which is stated in [13].
satisfies the (C) condition which is stated in [13].
Proof.
Suppose  satisfies
satisfies

In view of  , it suffices to prove that
, it suffices to prove that  is bounded in
is bounded in  . Similar to the proof of Lemma 2.6, we have
. Similar to the proof of Lemma 2.6, we have

Therefore  is an eigenfunction of
is an eigenfunction of  , then
, then  for a.e.
for a.e.  . It follows from
. It follows from  that
that

holds uniformly in  , which implies that
, which implies that

On the other hand, (2.34) implies that

Thus

which contradicts to (2.37). Hence  is bounded.
is bounded.
It is well known that critical groups and Morse theory are the main tools in solving elliptic partial differential equation. Let us recall some results which will be used later. We refer the readers to the book [14] for more information on Morse theory.
Let  be a Hilbert space, let
be a Hilbert space, let  be a functional satisfying the (PS) condition or (C) condition, let
be a functional satisfying the (PS) condition or (C) condition, let  be the
be the  th singular relative homology group with integer coefficients. Let
th singular relative homology group with integer coefficients. Let  be an isolated critical point of
be an isolated critical point of  with
with  and let
and let  be a neighborhood of
be a neighborhood of  . The group
. The group

is said to be the  th critical group of
th critical group of  at
at  , where
, where 
Let  be the set of critical points of
be the set of critical points of  and
and  ; the critical groups of
; the critical groups of  at infinity are formally defined by (see [15])
at infinity are formally defined by (see [15])

The following result comes from [14, 15] and will be used to prove the results in this paper.
Proposition 2.8 (see [15]).
Assume that 
 is bounded from below on
is bounded from below on  and
and  as
as  with
with  . Then
. Then

3. Proof of the Main Results
Proof of Theorem 2.1.
By Lemmas 2.32.4 and the mountain pass theorem, the functional  has a critical point
has a critical point  satisfying
satisfying  . Since
. Since  ,
,  , and by the maximum principle, we get
, and by the maximum principle, we get  . Hence
. Hence  is a positive solution of the problem (1.1) and satisfies
is a positive solution of the problem (1.1) and satisfies

Using the results in [14], we obtain

Similarly, we can obtain another negative critical point  of
of  satisfying
satisfying

Since  the zero function is a local minimizer of
the zero function is a local minimizer of  , and then
, and then

On the other hand, by Lemmas 2.52.6 and Proposition 2.8, we have

Hence  has a critical point
has a critical point  satisfying
satisfying

Since  , it follows from (3.2)–(3.6) that
, it follows from (3.2)–(3.6) that  ,
,  , and
, and  are three different nontrivial solutions of problem (1.1).
are three different nontrivial solutions of problem (1.1).
Proof of Theorem 2.2.
By Lemmas 2.52.7 and the Proposition 2.8, we can prove the conclusion (3.5). The other proof is similar to that of Theorem 2.1.
References
Ambrosetti A, Rabinowitz P: Dual variational methods in critical point theory and applications. Journal of Functional Analysis 1973, 14: 349-381. 10.1016/0022-1236(73)90051-7
Brézis H, Nirenberg L: Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Communications on Pure and Applied Mathematics 1983,36(4):437-477. 10.1002/cpa.3160360405
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMs Regional Conference Series in Mathematics, no. 65. American Mathematical Society, Providence, RI, USA; 1986.
Bernis F, García-Azorero J, Peral I: Existence and multiplicity of nontrivial solutions in semilinear critical problems of fourth order. Advances in Differential Equations 1996,1(2):219-240.
Deng YB, Wang GS: On inhomogeneous biharmonic equations involving critical exponents. Proceedings of the Royal Society of Edinburgh 1999,129(5):925-946. 10.1017/S0308210500031012
Gazzola F, Grunau H-C, Squassina M: Existence and nonexistence results for critical growth biharmonic elliptic equations. Calculus of Variations and Partial Differential Equations 2003,18(2):117-143. 10.1007/s00526-002-0182-9
Noussair ES, Swanson CA, Yang J:Critical semilinear biharmonic equations in
 . Proceedings of the Royal Society of Edinburgh 1992,121(1-2):139-148. 10.1017/S0308210500014189
. Proceedings of the Royal Society of Edinburgh 1992,121(1-2):139-148. 10.1017/S0308210500014189Zhou H-S: Existence of asymptotically linear Dirichlet problem. Nonlinear Analysis: Theory, Methods & Applications 2001, 44: 909-918. 10.1016/S0362-546X(99)00314-4
Stuart CA, Zhou HS:Applying the mountain pass theorem to an asymptotically linear elliptic equation on
 . Communications in Partial Differential Equations 1999,24(9-10):1731-1758. 10.1080/03605309908821481
. Communications in Partial Differential Equations 1999,24(9-10):1731-1758. 10.1080/03605309908821481Li GB, Zhou H-S:Multiple solutions to
 -Laplacian problems with asymptotic nonlinearity as
-Laplacian problems with asymptotic nonlinearity as  at infinity. Journal of the London Mathematical Society 2002,65(1):123-138. 10.1112/S0024610701002708
at infinity. Journal of the London Mathematical Society 2002,65(1):123-138. 10.1112/S0024610701002708Ziemer WP: Weakly Differentiable Functions, Graduate Texts in Mathematics. Volume 120. Springer, New York, NY, USA; 1989:xvi+308.
Liu Y, Wang ZP: Biharmonic equations with asymptotically linear nonlinearities. Acta Mathematica Scientia 2007,27(3):549-560. 10.1016/S0252-9602(07)60055-1
Su JB, Zhao LG: An elliptic resonance problem with multiple solutions. Journal of Mathematical Analysis and Applications 2006,319(2):604-616. 10.1016/j.jmaa.2005.10.059
Chang K-C: Infinite-Dimensional Morse Theory and Multiple Solution Problems. Birkhäuser, Boston, Mass, USA; 1993:x+312.
Bartsch T, Li SJ: Critical point theory for asymptotically quadratic functionals and applications to problems with resonance. Nonlinear Analysis: Theory, Methods & Applications 1997,28(3):419-441. 10.1016/0362-546X(95)00167-T
Acknowledgments
The author would like to thank the referees for valuable comments and suggestions for improving this paper. This work was supported by the National NSF (Grant no. 10671156) of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pei, R. Multiple Solutions for Biharmonic Equations with Asymptotically Linear Nonlinearities. Bound Value Probl 2010, 241518 (2010). https://doi.org/10.1155/2010/241518
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/241518
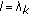 . Write
. Write 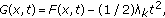
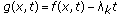 . Then
. Then 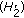 and
and 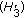 imply that
imply that 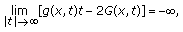
 . Proceedings of the Royal Society of Edinburgh 1992,121(1-2):139-148. 10.1017/S0308210500014189
. Proceedings of the Royal Society of Edinburgh 1992,121(1-2):139-148. 10.1017/S0308210500014189 . Communications in Partial Differential Equations 1999,24(9-10):1731-1758. 10.1080/03605309908821481
. Communications in Partial Differential Equations 1999,24(9-10):1731-1758. 10.1080/03605309908821481 -Laplacian problems with asymptotic nonlinearity as
-Laplacian problems with asymptotic nonlinearity as  at infinity. Journal of the London Mathematical Society 2002,65(1):123-138. 10.1112/S0024610701002708
at infinity. Journal of the London Mathematical Society 2002,65(1):123-138. 10.1112/S0024610701002708