- Research Article
- Open access
- Published:
Positive Solutions to Nonlinear First-Order Nonlocal BVPs with Parameter on Time Scales
Boundary Value Problems volume 2011, Article number: 198598 (2011)
Abstract
We discuss the existence of solutions for the first-order multipoint BVPs on time scale  :
:  ,
,  ,
,  , where
, where  is a parameter,
is a parameter,  is a fixed number,
is a fixed number,  ,
,  is continuous,
is continuous,  is regressive and rd-continuous,
is regressive and rd-continuous,  ,
,  ,
,  ,
,  , and
, and  . For suitable
. For suitable  , some existence, multiplicity, and nonexistence criteria of positive solutions are established by using well-known results from the fixed-point index.
, some existence, multiplicity, and nonexistence criteria of positive solutions are established by using well-known results from the fixed-point index.
1. Introduction
Let  be a time scale (a nonempty closed subset of the real line
be a time scale (a nonempty closed subset of the real line  ). We discuss the existence of positive solutions to the first-order multipoint BVPs on time scale
). We discuss the existence of positive solutions to the first-order multipoint BVPs on time scale  :
:

where  is a fixed number,
is a fixed number,  ,
,  is continuous,
is continuous,  is regressive and rd-continuous,
is regressive and rd-continuous,  , and
, and  ,
,  is defined in its standard form; see [1, page 59] for details.
is defined in its standard form; see [1, page 59] for details.
The multipoint boundary value problems arise in a variety of different areas of applied mathematics and physics. For example, the vibrations of a guy wire of a uniform cross-section and composed of  parts of different densities can be set up as a multipoint boundary value problem [2]; also many problems in the theory of elastic stability can be handled by a multipoint problem [3]. So, the existence of solutions to multipoint boundary value problems have been studied by many authors; see [4–13] and the reference therein. Especially, in recent years the existence of positive solutions to multipoint boundary value problems on time scales has caught considerable attention; see [10–14]. For other background on dynamic equations on time scales, one can see [1, 15–18].
parts of different densities can be set up as a multipoint boundary value problem [2]; also many problems in the theory of elastic stability can be handled by a multipoint problem [3]. So, the existence of solutions to multipoint boundary value problems have been studied by many authors; see [4–13] and the reference therein. Especially, in recent years the existence of positive solutions to multipoint boundary value problems on time scales has caught considerable attention; see [10–14]. For other background on dynamic equations on time scales, one can see [1, 15–18].
Our ideas arise from [13, 16]. In [13], Tian and Ge discussed the existence of positive solutions to nonlinear first-order three-point boundary value problems on time scale  :
:

where  is continuous,
is continuous,  is regressive and rd-continuous,
is regressive and rd-continuous,  and
and  . The existence results are based on Krasnoselskii's fixed-point theorem in cones and Leggett-Williams's theorem.
. The existence results are based on Krasnoselskii's fixed-point theorem in cones and Leggett-Williams's theorem.
As we can see, if we take  ,
, ,
, , and
, and  for
for  , then (1.1) is reduced to (1.2). Because of the influence of the parameter
, then (1.1) is reduced to (1.2). Because of the influence of the parameter  , it will be more difficult to solve (1.1) than to solve (1.2).
, it will be more difficult to solve (1.1) than to solve (1.2).
In 2009, by using the fixed-point index theory, Sun and Li [16] discussed the existence of positive solutions to the first-order PBVPs on time scale  :
:

For suitable  , they gave some existence, multiplicity, and nonexistence criteria of positive solutions.
, they gave some existence, multiplicity, and nonexistence criteria of positive solutions.
Motivated by the above results, by using the well-known fixed-point index theory [16, 19], we attempt to obtain some existence, multiplicity and nonexistence criteria of positive solutions to (1.1) for suitable  .
.
The rest of this paper is arranged as follows. Some preliminary results including Green's function are given in Section 2. In Section 3, we obtain some useful lemmas for the proof of the main result. In Section 4, some existence and multiplicity results are established. At last, some nonexistence results are given in Section 5.
2. Preliminaries
Throughout the rest of this paper, we make the following assumptions:
 is continuous and
is continuous and  for
for  ,
,
 is rd-continuous, which implies that
is rd-continuous, which implies that  (where
(where  is defined in [16, 18, 20]).
is defined in [16, 18, 20]).
Moreover, let

Our main tool is the well-known results from the fixed-point index, which we state here for the convenience of the reader.
Theorem 2.1 (see [19]).
Let  be a Banach space and
be a Banach space and  be a cone in
be a cone in  . For
. For  , we define
, we define  . Assume that
. Assume that  is completely continuous such
is completely continuous such  for
for  .
.
(i)If  for
for  , then
, then

(ii)If  for
for  , then
, then

Let  be equipped with the norm
be equipped with the norm  . It is easy to see that
. It is easy to see that  is a Banach space.
is a Banach space.
For  , we consider the following linear BVP:
, we consider the following linear BVP:


For  , define
, define

Lemma 2.2.
For  , the linear BVP (2.4)-(2.5) has a solution
, the linear BVP (2.4)-(2.5) has a solution  if and only if
if and only if  satisfies
satisfies

where

Proof.
By (2.4), we have

So,

And so,

Combining this with (2.5), we get

Lemma 2.3.
If the function  is defined in (2.7), then
is defined in (2.7), then  may be expressed by
may be expressed by

where

Proof.
When  ,
,

()For  ,
,

()For  ,
,

()For  ,
,

When  ,
,  ,
,

()For  ,
,

()For  ,
,

()For  ,
,

()For  ,
,

When  ,
,

()For  ,
,

()For  ,
,

()For  ,
,

Lemma 2.4.
Green's function  has the following properties.
has the following properties.
(i) ,
,
(ii) where
where 

(iii) ,
, 
Proof.
This proof is similar to [13, Lemma  ], so we omit it.
], so we omit it.
Now, we define a cone  in
in  as follows:
as follows:

where  . For
. For  , let
, let  and
and  .
.
For  , define an operator
, define an operator  :
:

Similar to the proof of [13, Lemma  ], we can see that
], we can see that  is completely continuous. By the above discussions, its not difficult to see that
is completely continuous. By the above discussions, its not difficult to see that  being a solution of BVP (1.1) equals the solution that
being a solution of BVP (1.1) equals the solution that  is a fixed point of the operator
is a fixed point of the operator  .
.
3. Some Lemmas
Lemma 3.1.
Let  . If
. If  and
and  ,
,  , then
, then

Proof.
Since  and
and  ,
,  , we have
, we have

Lemma 3.2.
Let  . If
. If  and
and  ,
,  , then
, then

Proof.
Since  and
and  ,
,  , we have
, we have

Lemma 3.3.
Let  . If
. If  , then
, then

where  ;
;  .
.
Proof.
Since  , we have
, we have  ,
,  . So,
. So,

4. Some Existence and Multiplicity Results
Theorem 4.1.
Assume that (H1) and (H2) hold and that  . Then the BVP (1.1) has at least two positive solutions for
. Then the BVP (1.1) has at least two positive solutions for

Proof.
Let  . Then it follows from (4.1) and Lemma 3.3 that
. Then it follows from (4.1) and Lemma 3.3 that

In view of Theorem 2.1, we have

Now, combined with the definition of  , we may choose
, we may choose  such that
such that  for
for  and
and  uniformly, where
uniformly, where  satisfies
satisfies

So,

In view of (4.1), (4.4), (4.5), and Lemma 3.2, we have

It follows from Theorem 2.1 that

By (4.3) and (4.7), we get

This shows that  has a fixed point in
has a fixed point in  , which is a positive solution of the BVP (1.1).
, which is a positive solution of the BVP (1.1).
Now, by the definition of  , there exits an
, there exits an  such that
such that  for
for  and
and  , where
, where  is chosen so that
is chosen so that

Let  . Then for
. Then for  ,
,  ,
,  . So,
. So,

In view of (4.1), (4.9), and Lemma 3.2, we have

It follows from Theorem 2.1 that

By (4.3) and (4.12), we get

This shows that  has a fixed point in
has a fixed point in  , which is another positive solution of the BVP (1.1).
, which is another positive solution of the BVP (1.1).
Similar to the proof of Theorem 4.1, we have the following results.
Theorem 4.2.
Suppose that (H1) and (H2) hold and

Then,
(i)equation (1.1) has at least one positive solution if  ,
,
(ii)equation (1.1) has at least one positive solution if  ,
,
(iii)equation (1.1) has at least two positive solutions if  .
.
Theorem 4.3.
Assume that (H1) and (H2) hold. If 
 , then the BVP (1.1) has at least two positive solutions for
, then the BVP (1.1) has at least two positive solutions for

Proof.
Let  . Then it follows from (4.15) and Lemma 3.3 that
. Then it follows from (4.15) and Lemma 3.3 that

In view of Theorem 2.1, we have

Since  , we may choose
, we may choose  such that
such that  for
for  and
and  , where
, where  satisfies
satisfies  So,
So,

In view of (4.15), (4.18), and Lemma 3.1, we have

It follows from Theorem 2.1 that

By (4.17) and (4.20), we get

This shows that  has a fixed point in
has a fixed point in  , which is a positive solution of the BVP (1.1).
, which is a positive solution of the BVP (1.1).
Now, by the definition of  , there exists an
, there exists an  such that
such that  for
for  and
and  , where
, where  satisfies
satisfies

Let  . Then for
. Then for  ,
,  ,
,  . So,
. So,

Combined with (4.22) and Lemma 3.1, we have

It follows from Theorem 2.1 that

By (4.17) and (4.25), we get

This shows that  has a fixed point in
has a fixed point in  , which is another positive solution of the BVP (1.1).
, which is another positive solution of the BVP (1.1).
Similar to the proof of Theorem 4.3, we have the following results.
Theorem 4.4.
Suppose that (H1) and (H2) hold and that

Then,
(i)equation (1.1) has at least one positive solution if  ,
,
(ii)equation (1.1) has at least one positive solution if  ,
,
-
(iii)
equation (1.1) has at least two positive solutions if
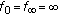 .
.
Theorem 4.5.
Suppose that (H1) and (H2) hold. If  , then the BVP (1.1) has at least one positive solution for
, then the BVP (1.1) has at least one positive solution for

Proof.
We only deal with the case that  ,
,  . The other three cases can be discussed similarly.
. The other three cases can be discussed similarly.
Let  satisfy (4.28) and let
satisfy (4.28) and let  be chosen such that
be chosen such that

From the definition of  , we know that there exists a constant
, we know that there exists a constant  such that
such that  for
for  and
and  . So,
. So,

This combines with (4.29) and Lemma 3.2, we have

It follows from Theorem 2.1 that

On the other hand, from the definition of  , there exists an
, there exists an  such that
such that  for
for  and
and  . Let
. Let  . Then for
. Then for  ,
,  ,
,  . So,
. So,

Combined with (4.29) and Lemma 3.1, we have

It follows from Theorem 2.1 that

By (4.32) and (4.35), we get

which implies that the BVP (1.1) has at least one positive solution in  .
.
Remark 4.6.
By making some minor modifications to the proof of Theorem 4.5, we can obtain the existence of at least one positive solution, if one of the following conditions is satisfied:
(i) ,
,  and
and .
.
(ii) ,
,  and
and .
.
(iii) ,
,  and
and .
.
(iv) ,
,  and
and .
.
Remark 4.7.
From Conditions (ii) and (iv) of Remark 4.6, we know that the conclusion in Theorem 4.5 holds for  in these two cases. By
in these two cases. By  and
and  , there exist two positive constants
, there exist two positive constants  such that, for
such that, for  ,
,

This is the condition of Theorem  of [13]. By
of [13]. By  and
and  , there exist two positive constants
, there exist two positive constants  such that for
such that for  ,
,

This is the condition of Theorem  of [13]. So, our conclusions extend and improve the results of [13].
of [13]. So, our conclusions extend and improve the results of [13].
5. Some Nonexistence Results
Theorem 5.1.
Assume that (H1) and (H2) hold. If  and
and  , then the BVP (1.1) has no positive solutions for sufficiently small
, then the BVP (1.1) has no positive solutions for sufficiently small  .
.
Proof.
In view of the definition of  , there exist positive constants
, there exist positive constants 
 ,
,  and
and  satisfying
satisfying  and
and

Let

Then  and we have
and we have

We assert that the BVP (1.1) has no positive solutions for  .
.
Suppose on the contrary that the BVP (1.1) has a positive solution  for
for  . Then from (5.3) and Lemma 3.2, we get
. Then from (5.3) and Lemma 3.2, we get

which is a contradiction.
Theorem 5.2.
Assume that (H1) and (H2) hold. If  and
and  , then the BVP (1.1) has no positive solutions for sufficiently large
, then the BVP (1.1) has no positive solutions for sufficiently large  .
.
Proof.
By the definition of  , there exist positive constants
, there exist positive constants 
 ,
,  , and
, and  satisfying
satisfying  ,
,  ,
,  , and
, and

Let

Then  and we have
and we have

We assert that the BVP (1.1) has no positive solutions for  .
.
Suppose on the contrary that the BVP (1.1) has a positive solution  for
for  . Then from (5.7) and Lemma 3.1 we get
. Then from (5.7) and Lemma 3.1 we get

which is a contradiction.
Corollary 5.3.
Assume that (H1) and (H2) hold. If  and
and  , then the BVP (1.1) has no positive solutions for sufficiently large
, then the BVP (1.1) has no positive solutions for sufficiently large  .
.
References
Sun J-P, Li W-T: Existence of solutions to nonlinear first-order PBVPs on time scales. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(3):883-888. 10.1016/j.na.2006.06.046
Moshinsky M: Sobre los problemas de condiciones a la frontiera en una dimension de caracteristicas discontinuas. Boletin Sociedad Matemática Mexicana 1950, 7: l-25.
Timoshenko SP: Theory of Elastic Stability. 2nd edition. McGraw-Hill, New York, NY, USA; 1961:xvi+541.
Rodriguez J, Taylor P: Scalar discrete nonlinear multipoint boundary value problems. Journal of Mathematical Analysis and Applications 2007, 330(2):876-890. 10.1016/j.jmaa.2006.08.008
Ma R: Positive solutions for a nonlinear three-point boundary-value problem. Electronic Journal of Differential Equations 1999, 34: 1-8.
Ma R: Multiplicity of positive solutions for second-order three-point boundary value problems. Computers & Mathematics with Applications 2000, 40(2-3):193-204. 10.1016/S0898-1221(00)00153-X
Ma R: Existence and uniqueness of solutions to first-order three-point boundary value problems. Applied Mathematics Letters 2002, 15(2):211-216. 10.1016/S0893-9659(01)00120-3
Ma R:Positive solutions for nonhomogeneous
 -point boundary value problems. Computers & Mathematics with Applications 2004, 47(4-5):689-698. 10.1016/S0898-1221(04)90056-9
-point boundary value problems. Computers & Mathematics with Applications 2004, 47(4-5):689-698. 10.1016/S0898-1221(04)90056-9Liu B: Existence and uniqueness of solutions to first-order multipoint boundary value problems. Applied Mathematics Letters 2004, 17(11):1307-1316. 10.1016/j.aml.2003.08.014
Anderson DR, Wong PJY: Positive solutions for second-order semipositone problems on time scales. Computers & Mathematics with Applications 2009, 58(2):281-291. 10.1016/j.camwa.2009.02.033
Luo H: Positive solutions to singular multi-point dynamic eigenvalue problems with mixed derivatives. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(4):1679-1691. 10.1016/j.na.2008.02.051
Luo H, Ma Q: Positive solutions to a generalized second-order three-point boundary-value problem on time scales. Electronic Journal of Differential Equations 2005, 2005(17):-14.
Tian Y, Ge W: Existence and uniqueness results for nonlinear first-order three-point boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):2833-2842. 10.1016/j.na.2007.08.054
Sun J-P: Existence of positive solution to second-order three-point BVPs on time scales. Boundary Value Problems 2009, 2009:-6.
Cabada A, Vivero DR: Existence of solutions of first-order dynamic equations with nonlinear functional boundary value conditions. Nonlinear Analysis: Theory, Methods & Applications 2005, 63(5–7):e697-e706.
Sun J-P, Li W-T: Positive solutions to nonlinear first-order PBVPs with parameter on time scales. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(3):1133-1145. 10.1016/j.na.2008.02.007
Sun J-P, Li W-T: Existence and multiplicity of positive solutions to nonlinear first-order PBVPs on time scales. Computers & Mathematics with Applications 2007, 54(6):861-871. 10.1016/j.camwa.2007.03.009
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xvi+541.
Acknowledgments
This work was supported by the NSFC Young Item (no. 70901016), HSSF of Ministry of Education of China (no. 09YJA790028), Program for Innovative Research Team of Liaoning Educational Committee (no. 2008T054), the NSF of Liaoning Province (no. L09DJY065), and NWNU-LKQN-09-3
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gao, C., Luo, H. Positive Solutions to Nonlinear First-Order Nonlocal BVPs with Parameter on Time Scales. Bound Value Probl 2011, 198598 (2011). https://doi.org/10.1155/2011/198598
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/198598
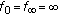 .
. -point boundary value problems. Computers & Mathematics with Applications 2004, 47(4-5):689-698. 10.1016/S0898-1221(04)90056-9
-point boundary value problems. Computers & Mathematics with Applications 2004, 47(4-5):689-698. 10.1016/S0898-1221(04)90056-9