- Research Article
- Open access
- Published:
Existence and Lyapunov Stability of Periodic Solutions for Generalized Higher-Order Neutral Differential Equations
Boundary Value Problems volume 2011, Article number: 635767 (2011)
Abstract
Existence and Lyapunov stability of periodic solutions for a generalized higher-order neutral differential equation are established.
1. Introduction
In recent years, there is a good amount of work on periodic solutions for neutral differential equations (see [1–11] and the references cited therein). For example, the following neutral differential equations

have been studied in [1, 3, 8], respectively, and existence criteria of periodic solutions were established for these equations. Afterwards, along with intensive research on the  -Laplacian, some authors [4, 11] start to consider the following
-Laplacian, some authors [4, 11] start to consider the following  -Laplacian neutral functional differential equations:
-Laplacian neutral functional differential equations:

and by using topological degree theory and some analysis skills, existence results of periodic solutions for (1.2) have been presented.
In general, most of the existing results are concentrated on lower-order neutral functional differential equations, while studies on higher-order neutral functional differential equations are rather infrequent, especially on higher-order  -Laplacian neutral functional differential equations. In this paper, we consider the following generalized higher-order neutral functional differential equation:
-Laplacian neutral functional differential equations. In this paper, we consider the following generalized higher-order neutral functional differential equation:

where  is given by
is given by  with
with  being a constant,
being a constant,  is a continuous function defined on
is a continuous function defined on  and is periodic with respect to
and is periodic with respect to  with period
with period  , that is,
, that is,  for all
for all  , and
, and  ,
,  are constants.
are constants.
Since the neutral operator is divided into two cases  and
and  , it is natural to study the neutral differential equation separately according to these two cases. The case
, it is natural to study the neutral differential equation separately according to these two cases. The case  has been studied in [5]. Now we consider (1.3) for the case
has been studied in [5]. Now we consider (1.3) for the case  . So throughout this paper, we always assume that
. So throughout this paper, we always assume that  , and the paper is organized as follows. We first transform (1.3) into a system of first-order differential equations, and then by applying Mawhin's continuation theory and some new inequalities, we obtain sufficient conditions for the existence of periodic solutions for (1.3). The Lyapunov stability of periodic solutions for the equation will then be established. Finally, an example is given to illustrate our results.
, and the paper is organized as follows. We first transform (1.3) into a system of first-order differential equations, and then by applying Mawhin's continuation theory and some new inequalities, we obtain sufficient conditions for the existence of periodic solutions for (1.3). The Lyapunov stability of periodic solutions for the equation will then be established. Finally, an example is given to illustrate our results.
2. Preparation
First, we recall two lemmas. Let  and
and  be real Banach spaces and let
be real Banach spaces and let  be a Fredholm operator with index zero; here
be a Fredholm operator with index zero; here  denotes the domain of
denotes the domain of  . This means that
. This means that  is closed in
is closed in  and
and  . Consider supplementary subspaces
. Consider supplementary subspaces  ,
,  of
of  ,
,  , respectively, such that
, respectively, such that  ,
,  . Let
. Let  and
and  denote the natural projections. Clearly,
denote the natural projections. Clearly,  and so the restriction
and so the restriction  is invertible. Let
is invertible. Let  denote the inverse of
denote the inverse of  .
.
Let  be an open bounded subset of
be an open bounded subset of  with
with  . A map
. A map  is said to be
is said to be  -compact in
-compact in  if
if  is bounded and the operator
is bounded and the operator  is compact.
is compact.
Lemma 2.1 (see [12]).
Suppose that  and
and  are two Banach spaces, and suppose that
are two Banach spaces, and suppose that  is a Fredholm operator with index zero. Let
is a Fredholm operator with index zero. Let  be an open bounded set and let
be an open bounded set and let  be
be  -compact on
-compact on  . Assume that the following conditions hold:
. Assume that the following conditions hold:
(1)
(2)
(3) , where
, where  is an isomorphism.
is an isomorphism.
Then, the equation  has a solution in
has a solution in  .
.
Lemma 2.2 (see [13]).
If  and
and  , then
, then

where  is a fixed real number with
is a fixed real number with  and
and

For the sake of convenience, throughout this paper we denote by  a positive real number, and for any continuous function
a positive real number, and for any continuous function  , we write
, we write

Let  be the operator on
be the operator on  given by
given by

Lemma 2.3.
The operator  has a continuous inverse
has a continuous inverse  on
on  satisfying the following:
satisfying the following:



Remark 2.4.
This lemma is basically proved in [3, 10]. For the convenience of the readers, we present a detailed proof here as follows.
Proof.
We split it into the following two cases.
Case 1 ( ).
).
Define an operator  by
by

Clearly,  and
and  . Note also that
. Note also that  . Therefore,
. Therefore,  has a continuous inverse
has a continuous inverse  with
with  ; here
; here  . Hence,
. Hence,

and so

Case 2 ( ).
).
Define operators

From the definition of the linear operator  , we have
, we have

Since  , the operator
, the operator  has a bounded inverse
has a bounded inverse  with
with

and so, for any  ,
,

On the other hand, from  , we have
, we have

That is,

Now, for any  , if
, if  satisfies
satisfies

then we have

or

So, we have

So,  exists and satisfies
exists and satisfies

This proves (1) and (2) of Lemma 2.3. Finally, (3) is easily verified.
By Hale's terminology [14], a solution  of (1.3) is that
of (1.3) is that  such that
such that  and (1.3) is satisfied on
and (1.3) is satisfied on  . In general,
. In general,  does not belong to
does not belong to  But we can see easily from
But we can see easily from  that a solution
that a solution  of (1.3) must belong to
of (1.3) must belong to  . Equation (1.3) is transformed into
. Equation (1.3) is transformed into

Lemma 2.5 (see [4]).
If  , then
, then

Now we consider (2.22). Define the conjugate index  by
by  . Introducing new variables
. Introducing new variables

Using the fact that  and by Lemma 2.3, (1.3) can be rewritten as
and by Lemma 2.3, (1.3) can be rewritten as

It is clear that, if  is a
is a  -periodic solution to (2.25), then
-periodic solution to (2.25), then  must be a
must be a  -periodic solution to (1.3). Thus, the problem of finding a
-periodic solution to (1.3). Thus, the problem of finding a  -periodic solution for (1.3) reduces to finding one for (2.25).
-periodic solution for (1.3) reduces to finding one for (2.25).
Define the linear spaces

with norm  . Obviously,
. Obviously,  and
and  are Banach spaces. Define
are Banach spaces. Define

by

Moreover, define

by

Then, (2.25) can be rewritten as the abstract equation  . From the definition of
. From the definition of  , one can easily see that
, one can easily see that  and
and  . So,
. So,  is a Fredholm operator with index zero. Let
is a Fredholm operator with index zero. Let  and
and  be defined by
be defined by

It is easy to see that  . Moreover, for all
. Moreover, for all  , if we write
, if we write  , we have
, we have  and so
and so  . This is to say
. This is to say  and
and  So,
So,  is a Fredholm operator with index zero. Let
is a Fredholm operator with index zero. Let  denote the inverse of
denote the inverse of  , then we have
, then we have

where

From (2.30) and (2.33), it is clear that  and
and  are continuous, and
are continuous, and  is bounded, and so
is bounded, and so  is compact for any open bounded
is compact for any open bounded  . Hence,
. Hence,  is
is  -compact on
-compact on  . For the function
. For the function  defined as (2.24), we have the following.
defined as (2.24), we have the following.
Lemma 2.6.
If  and
and  , then
, then

where 
Proof.
From  , there is a point
, there is a point  such that
such that  . Let
. Let  . Then,
. Then,  . From
. From  , there is a point
, there is a point  such that
such that  . Let
. Let  . Then,
. Then,  Continuing this way, we get from
Continuing this way, we get from  a point
a point  such that
such that  . Let
. Let  . Then,
. Then,  From
From  , we have
, we have  , so there is a point
, so there is a point  such that
such that  ; hence, we have
; hence, we have  . Let
. Let  . Then,
. Then,  Continuing this way, we get from
Continuing this way, we get from  that there is a point
that there is a point  such that
such that  . Let
. Let  . Then,
. Then,  By Lemma 2.2, we have
By Lemma 2.2, we have

By Lemma 2.5 and Lemma 2.2, we have

Combining (2.35) and (2.36), we get

Similarly, we get

This completes the proof of Lemma 2.6.
Remark 2.7.
In particular, if we take  , then
, then  and
and

In this case, (2.34) is transformed into

3. Main Results
For the sake of convenience, we list the following assumptions which will be used repeatedly in the sequel.
(H1)There exists a constant  such that
such that

H2There exists a constant  such that
such that

H3 There exist nonnegative constants  such that
such that

H4 There exist nonnegative constants  such that
such that

for all  .
.
Theorem 3.1.
If  and
and  hold, then (1.3) has at least one nonconstant
hold, then (1.3) has at least one nonconstant  -periodic solution.
-periodic solution.
Proof.
Consider the equation

Let  . If
. If  , then
, then

We first claim that there exists a constant  such that
such that

Integrating the last equation of (3.6) over  , we have
, we have

By the continuity of  , there exists
, there exists  such that
such that

From assumption  , we get (3.7). As a consequence, we have
, we get (3.7). As a consequence, we have

On the other hand, multiplying both sides of the last equation of (3.6) by  and integrating over
and integrating over  , using assumption
, using assumption  we have
we have

It is easy to see that there exists a constant  (independent of
(independent of  ) such that
) such that

From  , there exists a point
, there exists a point  such that
such that  . By Hölder's inequality, we have
. By Hölder's inequality, we have

From  , there exists a point
, there exists a point  such that
such that  , and we have
, and we have

Continuing this way for  , we get
, we get

Hence,

Meanwhile, from (3.10), we get

Let  . Then, obviously
. Then, obviously  ,
,  and
and  .
.
Let  . If
. If  , then
, then  , which means that
, which means that  and
and  . We see that
. We see that

So,

Now take  . By the analysis above, it is easy to see that
. By the analysis above, it is easy to see that  ,
,  , and conditions (1) and (2) of Lemma 2.1 are satisfied.
, and conditions (1) and (2) of Lemma 2.1 are satisfied.
Next we show that condition (3) of Lemma 2.1 is also satisfied. Define an isomorphism  as follows:
as follows:

Let  ,
,  . Then, for all
. Then, for all  ,
,

From  , it is obvious that
, it is obvious that  for all
for all  . Therefore,
. Therefore,

which means that condition (3) of Lemma 2.1 is also satisfied. By applying Lemma 2.1, we conclude that equation  has a solution
has a solution  on
on  ; that is, (1.3) has a
; that is, (1.3) has a  -periodic solution
-periodic solution  with
with  .
.
Finally, observe that  is not constant. For, if
is not constant. For, if  (constant), then from (1.3) we have
(constant), then from (1.3) we have  , which contradicts the assumption that
, which contradicts the assumption that  . The proof is complete.
. The proof is complete.
Theorem 3.2.
If  and
and  hold, then (1.3) has at least one nonconstant
hold, then (1.3) has at least one nonconstant  -periodic solution if one of the following conditions holds:
-periodic solution if one of the following conditions holds:
(1) ,
,
(2) and
and 
Proof.
Let  be defined as in Theorem 3.1. If
be defined as in Theorem 3.1. If  then from the proof of Theorem 3.1 we have
then from the proof of Theorem 3.1 we have


We claim that  is bounded.
is bounded.
Multiplying both sides of (3.23) by  and integrating over
and integrating over  , by using assumption
, by using assumption  we have
we have

Applying Hölder's inequality, we have

Applying Lemma 2.6 and (3.26), we have

Case 1.
If  and
and  , then it is easy to see that there exists a constant
, then it is easy to see that there exists a constant  (independent of
(independent of  ) such that
) such that

Case 2.
If  , then it is easy to see that there exists a constant
, then it is easy to see that there exists a constant  (independent of
(independent of  ) such that
) such that

From  , there exists a point
, there exists a point  such that
such that  . By Hölder's inequality, we have
. By Hölder's inequality, we have

This proves the claim, and the rest of the proof of the theorem is identical to that of Theorem 3.1.
Remark 3.3.
If (1.3) takes the form

where  and
and  , then the results of Theorems 3.1 and 3.2 still hold.
, then the results of Theorems 3.1 and 3.2 still hold.
Remark 3.4.
If  , then (1.3) is transformed into
, then (1.3) is transformed into

and the results of Theorems 3.1 and 3.2 still hold.
Next, we study the Lyapunov stability of the periodic solutions of (3.32).
Theorem 3.5.
Assume that  holds. Then every
holds. Then every  -periodic solution of (3.32) is Lyapunov stable.
-periodic solution of (3.32) is Lyapunov stable.
Proof.
Let

Then, system (3.32) is transformed into

Suppose now that  is a
is a  -periodic solution of (3.34). Let
-periodic solution of (3.34). Let  be any arbitrary solution of (3.34). For any
be any arbitrary solution of (3.34). For any  , write
, write  . Then, it follows from (3.34) that
. Then, it follows from (3.34) that

and so

Let  . Then,
. Then,

Take  , and define a function
, and define a function  by
by

Let  . It is obvious that
. It is obvious that  and
and  . From
. From  and Lemma 2.3, we get
and Lemma 2.3, we get

Hence,  is a Lyapunov function for nonautonomous (3.32) (see [15, page 50]), and so the
is a Lyapunov function for nonautonomous (3.32) (see [15, page 50]), and so the  -periodic solution
-periodic solution  of (3.32) is Lyapunov stable.
of (3.32) is Lyapunov stable.
Finally, we present an example to illustrate our result.
Example 3.6.
Consider the  -order delay differential equation
-order delay differential equation

Here  is a constant with
is a constant with  . Comparing with (1.3), we have
. Comparing with (1.3), we have  and
and

Observe that  has period
has period  and satisfies
and satisfies

Pick  . Then,
. Then,

for all  with
with  . Hence,
. Hence,  holds. On the other hand, since
holds. On the other hand, since

assumption  holds with
holds with  .
.
Case 1.
If  , then by (1) of Theorem 3.2, (3.40) has at least one nonconstant
, then by (1) of Theorem 3.2, (3.40) has at least one nonconstant  -periodic solution.
-periodic solution.
Case 2.
If  , then
, then

So by (2) of Theorem 3.2, (3.40) has at least one nonconstant  -periodic solution.
-periodic solution.
References
Lu S, Ge W: On the existence of periodic solutions for neutral functional differential equation. Nonlinear Analysis: Theory, Methods & Applications 2003, 54(7):1285-1306. 10.1016/S0362-546X(03)00187-1
Lu S:Existence of periodic solutions for a
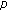 -Laplacian neutral functional differential equation. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):231-243. 10.1016/j.na.2007.11.053
-Laplacian neutral functional differential equation. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):231-243. 10.1016/j.na.2007.11.053Lu S, Ge W, Zheng Z: Periodic solutions to neutral differential equation with deviating arguments. Applied Mathematics and Computation 2004, 152(1):17-27. 10.1016/S0096-3003(03)00530-7
Peng S:Periodic solutions for
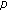 -Laplacian neutral Rayleigh equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5-6):1675-1685. 10.1016/j.na.2007.07.007
-Laplacian neutral Rayleigh equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5-6):1675-1685. 10.1016/j.na.2007.07.007Ren J, Cheng Z: Periodic solutions for generalized high-order neutral differential equation in the critical case. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(12):6182-6193. 10.1016/j.na.2009.06.011
Shen J, Liang R: Periodic solutions for a kind of second order neutral functional differential equations. Applied Mathematics and Computation 2007, 190(2):1394-1401. 10.1016/j.amc.2007.02.137
Wang Q, Dai B: Three periodic solutions of nonlinear neutral functional differential equations. Nonlinear Analysis: Real World Applications 2008, 9(3):977-984. 10.1016/j.nonrwa.2007.01.014
Wang K, Lu S: On the existence of periodic solutions for a kind of high-order neutral functional differential equation. Journal of Mathematical Analysis and Applications 2007, 326(2):1161-1173. 10.1016/j.jmaa.2006.03.078
Wu J, Wang Z: Two periodic solutions of second-order neutral functional differential equations. Journal of Mathematical Analysis and Applications 2007, 329(1):677-689. 10.1016/j.jmaa.2006.06.084
Zhang MR: Periodic solutions of linear and quasilinear neutral functional-differential equations. Journal of Mathematical Analysis and Applications 1995, 189(2):378-392. 10.1006/jmaa.1995.1025
Zhu Y, Lu S:Periodic solutions for
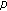 -Laplacian neutral functional differential equation with deviating arguments. Journal of Mathematical Analysis and Applications 2007, 325(1):377-385. 10.1016/j.jmaa.2005.10.084
-Laplacian neutral functional differential equation with deviating arguments. Journal of Mathematical Analysis and Applications 2007, 325(1):377-385. 10.1016/j.jmaa.2005.10.084Gaines RE, Mawhin JL: Coincidence Degree, and Nonlinear Differential Equations, Lecture Notes in Mathematics, vol. 568. Springer, Berlin, Germany; 1977:i+262.
Zhang M:Nonuniform nonresonance at the first eigenvalue of the
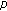 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1997, 29(1):41-51. 10.1016/S0362-546X(96)00037-5
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1997, 29(1):41-51. 10.1016/S0362-546X(96)00037-5Hale JK: Theory of Functional Differential Equations. Springer, New York, NY, USA; 1977.
Glendinning P: Stability, Instability and Chaos: An Introduction to the Theory of Nonlinear Differential Equations, Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge, UK; 1994:xiv+388.
Acknowledgments
This paper is partially supported by the National Natural Science Foundation of China (10971202), and the Research Grant Council of Hong Kong SAR, China (project no. HKU7016/07P).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ren, J., Cheung, WS. & Cheng, Z. Existence and Lyapunov Stability of Periodic Solutions for Generalized Higher-Order Neutral Differential Equations. Bound Value Probl 2011, 635767 (2011). https://doi.org/10.1155/2011/635767
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/635767
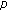 -Laplacian neutral functional differential equation. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):231-243. 10.1016/j.na.2007.11.053
-Laplacian neutral functional differential equation. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):231-243. 10.1016/j.na.2007.11.053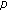 -Laplacian neutral Rayleigh equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5-6):1675-1685. 10.1016/j.na.2007.07.007
-Laplacian neutral Rayleigh equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5-6):1675-1685. 10.1016/j.na.2007.07.007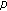 -Laplacian neutral functional differential equation with deviating arguments. Journal of Mathematical Analysis and Applications 2007, 325(1):377-385. 10.1016/j.jmaa.2005.10.084
-Laplacian neutral functional differential equation with deviating arguments. Journal of Mathematical Analysis and Applications 2007, 325(1):377-385. 10.1016/j.jmaa.2005.10.084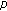 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1997, 29(1):41-51. 10.1016/S0362-546X(96)00037-5
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1997, 29(1):41-51. 10.1016/S0362-546X(96)00037-5