- Research Article
- Open access
- Published:
Existence Results of Three-Point Boundary Value Problems for Second-order Ordinary Differential Equations
Boundary Value Problems volume 2011, Article number: 901796 (2011)
Abstract
We establish existence results of the following three-point boundary value problems:  ,
,  ,
,  and
and  , where
, where  and
and  . The approach applied in this paper is upper and lower solution method associated with basic degree theory or Schauder's fixed point theorem. We deal with this problem with the function
. The approach applied in this paper is upper and lower solution method associated with basic degree theory or Schauder's fixed point theorem. We deal with this problem with the function  which is Carathéodory or singular on its domain.
which is Carathéodory or singular on its domain.
1. Introduction
In this paper, we consider three-point boundary value problem


where  and
and  .
.
In the mathematical literature, a number of works have appeared on nonlocal boundary value problems, and one of the first of these was [1]. Il'in and Moiseev initiated the research of multipoint boundary value problems for second-order linear ordinary differential equations, see [2, 3], motivated by the study [4–6] of Bitsadze and Samarskii.
Recently, nonlinear multipoint boundary value problems have been receiving considerable attention, and have been studied extensively by using iteration scheme (e.g., [7]), fixed point theorems in cones (e.g., [8]), and the Leray-Schauder continuation theorem (e.g., [9]). We refer more detailed treatment to more interesting research [10, 11] and the references therein.
The theory of upper and lower solutions is also a powerful tool in studying boundary value problems. For the existence results of two-point boundary value problem, there already are lots of interesting works by applying this essential technique (see [12, 13]). Recently, it is shown that this method plays an important role in proving the existence of solutions for three-point boundary value problems (see [14–16]).
Last but not least, as the singular source term appearing in two-point problems, singular three-point boundary value problems also attract more attention (e.g., [17]).
In this paper, we will discuss the existence of solutions of some general types on three-point boundary value problems by using upper and lower solution method associated with basic degree theory or Schauder's fixed point theorem.
This paper is organized as follows. In Section 2, we give two lemmas which will be extensively used later. In Section 3, when the source term  is a Carathéodory function, we consider the Sobolev space
is a Carathéodory function, we consider the Sobolev space  defined by
defined by

and obtain the existence of  -solution in Theorems 3.5 and 3.11. In Section 4, we discuss the singular case, that is,
-solution in Theorems 3.5 and 3.11. In Section 4, we discuss the singular case, that is,  maybe singular at the end points
maybe singular at the end points  or
or  , or at
, or at  . We will introduce the
. We will introduce the  -class of functions and another space
-class of functions and another space  (see [18, 19]) as follows:
(see [18, 19]) as follows:

and prove the existence of  -solution in Theorems 4.1 and 4.4. Some sufficient conditions for constructing upper and lower solutions are given in each section for applications.
-solution in Theorems 4.1 and 4.4. Some sufficient conditions for constructing upper and lower solutions are given in each section for applications.
2. Preliminaries
Define  by
by

where  and
and  are given as (1.2) and
are given as (1.2) and

By direct computations, we get the following results.
Lemma 2.1.
-
(i)
The function
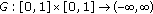 defined by (2.1), is the Green function corresponding for the problem
defined by (2.1), is the Green function corresponding for the problem 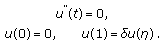 (2.3)
(2.3)
(ii) The function  defined by (2.1), is continuous.
defined by (2.1), is continuous.
-
(iii)
In the case
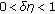 , we have
, we have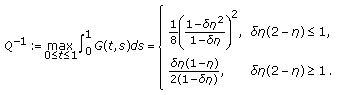 (2.4)
(2.4)
Lemma 2.2.
If  , then the problem
, then the problem

with boundary condition (1.2) has a unique solution  such that
such that

where  is defined by (2.1).
is defined by (2.1).
3. Carathéodory Case
In this section we first introduce the Carathéodory function as follows.
Definition 3.1.
A function  defined on
defined on  is called a Carathéodory function on
is called a Carathéodory function on  if
if
(i)for almost every 
 is continuous on
is continuous on  ;
;
(ii)for any  the function
the function  is measurable on
is measurable on  ;
;
(iii)for any  , there exists
, there exists  such that for any
such that for any  and for almost every
and for almost every  with
with  , we have
, we have  .
.
We in this section assume that  is a Carathéodory function and discuss the existence of
is a Carathéodory function and discuss the existence of  -solution by assuming the existence of upper and lower solutions.
-solution by assuming the existence of upper and lower solutions.
3.1. Existence of  -Solutions
-Solutions
We first introduce the definitions of  -upper and lower solutions as below.
-upper and lower solutions as below.
Definition 3.2.
A function  is called a
is called a  -lower solution of problem (1.1) and (1.2) if it satisfies
-lower solution of problem (1.1) and (1.2) if it satisfies
(i) ,
,  , and
, and
(ii)for any  , either
, either  , or there exists an open interval
, or there exists an open interval  containing
containing  such that
such that  and, for almost every
and, for almost every  , we have
, we have

Definition 3.3.
A function  is called a
is called a  -upper solution of problem (1.1) and (1.2) if it satisfies
-upper solution of problem (1.1) and (1.2) if it satisfies
(i) ,
,  , and
, and
(ii)for any  , either
, either  , or there exists an open interval
, or there exists an open interval  containing
containing  such that
such that  and, for almost every
and, for almost every  , we have
, we have

Before proving our main results, we first consider such a modified problem given as follows:

with boundary condition (1.2), where  is defined by
is defined by

Proposition 3.4.
Let  and
and  be respective
be respective  -lower and upper solutions of problem (1.1) and (1.2) with
-lower and upper solutions of problem (1.1) and (1.2) with  on
on  . If
. If  is a solution of problem (3.3) and (1.2), then
is a solution of problem (3.3) and (1.2), then  , for any
, for any  .
.
Proof.
Suppose there exists  such that
such that

Case 1.
If  , we have
, we have  , which implies
, which implies  Hence, by Definition 3.2 and the continuity of
Hence, by Definition 3.2 and the continuity of  at
at  , there exist an open interval
, there exist an open interval  with
with  ,
,  and a neighborhood
and a neighborhood  of
of  contained in
contained in  such that for almost every
such that for almost every  ,
,

Furthermore, it follows from  that for
that for  ,
,  , we have
, we have

This implies that the minimum of  cannot occur at
cannot occur at  , a contradiction.
, a contradiction.
Case 2.
If  , by the definition of
, by the definition of  -lower solution
-lower solution  , we then have
, we then have

And we get a contradiction.
Case 3.
If  , it follows from the conclusion of Case 1 that
, it follows from the conclusion of Case 1 that

which is impossible.
Consequently, we obtain  on
on  . By the similar arguments as above, we also have
. By the similar arguments as above, we also have

Theorem 3.5.
Let  and
and  be
be  -lower and upper solutions of problem (1.1) and (1.2) such that
-lower and upper solutions of problem (1.1) and (1.2) such that  on
on  and let
and let  be a Carathéodory function on
be a Carathéodory function on  , where
, where

Then problem (1.1) and (1.2) has at least one solution  such that, for all
such that, for all  ,
,

Proof.
We consider the modified problem (3.3) and (1.2) with respect to the given  and
and  . Consider the Banach space
. Consider the Banach space  with supremum and the operator
with supremum and the operator  by
by

for  , where
, where  is defined as (2.1). Since
is defined as (2.1). Since  is a Carathéodory function on
is a Carathéodory function on  , for almost all
, for almost all  and for all
and for all  , there exists a function
, there exists a function  , we have
, we have

Define

where


It is clear that  is a closed, bounded and convex set in
is a closed, bounded and convex set in  and one can show that
and one can show that  is a completely continuous mapping by Arzelà-Ascoli theorem and Lebesgue dominated convergence theorem. By applying Schauder's fixed point theorem, we obtain that
is a completely continuous mapping by Arzelà-Ascoli theorem and Lebesgue dominated convergence theorem. By applying Schauder's fixed point theorem, we obtain that  has a fixed point in
has a fixed point in  which is a solution of problem (3.3) and (1.2). From Proposition 3.4, this fixed point is also a solution of problem (1.1) and (1.2). Hence, we complete the proof.
which is a solution of problem (3.3) and (1.2). From Proposition 3.4, this fixed point is also a solution of problem (1.1) and (1.2). Hence, we complete the proof.
We further illustrate the use of Theorem 3.11 in the following second-order differential equation:

with the boundary condition (1.2).
Corollary 3.6.
Assume that  is a Carathéodory function satisfying
is a Carathéodory function satisfying  is essentially bounded for
is essentially bounded for  , where
, where  is a constant large enough. Assume further that
is a constant large enough. Assume further that  and there exists a constant
and there exists a constant  such that
such that

Then, problem (3.18) and (1.2) has at least one solution.
Proof.
By hypothesis, for any given  small enough such that
small enough such that  and for almost all
and for almost all  , for any
, for any  large enough, we have
large enough, we have

We now choose an upper solution  of the form
of the form

To this end, we compute

Clearly, one can choose  such that
such that

that is,

and choose  , where
, where  , which is a positive solution of
, which is a positive solution of

Hence, if  is large enough, we can show that
is large enough, we can show that  and
and  , where
, where  , which implies that
, which implies that  is a positive
is a positive  -upper solution. In the same way we construct a
-upper solution. In the same way we construct a  -lower solution
-lower solution  on
on  .
.
3.2. Nontangency Solution
In this subsection, we afford another stronger lower and upper solutions to get a strict inequality of the solution between them.
Definition 3.7.
A function  is a strict
is a strict  -lower solution of problem (1.1) and (1.2), if it is not a solution of problem (1.1) and (1.2),
-lower solution of problem (1.1) and (1.2), if it is not a solution of problem (1.1) and (1.2),  ,
,  and for any
and for any  , one of the following is satisfied:
, one of the following is satisfied:
(i) ;
;
(ii)there exist an interval  and
and  such that
such that  int
int ,
,  and for almost every
and for almost every  , for all
, for all  we have
we have

Definition 3.8.
A function  is a strict
is a strict  -upper solution of problem (1.1) and (1.2), if it is not a solution of problem (1.1) and (1.2),
-upper solution of problem (1.1) and (1.2), if it is not a solution of problem (1.1) and (1.2),  ,
,  and for any
and for any  , one of the following is satisfied:
, one of the following is satisfied:
(i) ,
,
(ii)there exist an interval  and
and  such that
such that  int
int ,
,  and for almost every
and for almost every  , for all
, for all  we have
we have

Remark 3.9.
Every strict  -lower(upper) solution of problem (1.1) and (1.2) is a
-lower(upper) solution of problem (1.1) and (1.2) is a  -lower(upper) solution.
-lower(upper) solution.
Now we are going to show that the solution curve of problem (1.1) and (1.2) cannot be tangent to upper or lower solutions from below or above.
Proposition 3.10.
Let  and
and  be respective strict
be respective strict  -lower and upper solutions of problem (1.1) and (1.2) with
-lower and upper solutions of problem (1.1) and (1.2) with  on
on  . If
. If  is a solution of problem (1.1) and (1.2) with
is a solution of problem (1.1) and (1.2) with  on
on  , then
, then  , for any
, for any  .
.
Proof.
As  is not a solution,
is not a solution,  is not identical to
is not identical to  . Assume, the conclusion does not hold, then
. Assume, the conclusion does not hold, then

exists. Hence,  has minimum at
has minimum at  , that is,
, that is,  .
.
Case 1.
Set  . Since
. Since  has minimum at
has minimum at  , we have
, we have  . According to the Definition 3.7, there exist
. According to the Definition 3.7, there exist  ,
,  and
and  with
with  such that, for every
such that, for every  ,
,  ,
,  and for a.e.
and for a.e. 

Hence, we have the contradiction since

Case 2.
If  , by the definition of strict
, by the definition of strict  -lower solution that
-lower solution that  , we then have
, we then have

And we get a contradiction.
Case 3.
If  , repeat the same arguments in Case 3 of the proof of Proposition 3.4. Therefore, we obtain
, repeat the same arguments in Case 3 of the proof of Proposition 3.4. Therefore, we obtain  on
on  . The inequality
. The inequality  on
on  can be proved by the similar arguments as above.
can be proved by the similar arguments as above.
Theorem 3.11.
Let  and
and  be strict
be strict  -lower and upper solutions of problem (1.1) and (1.2) such that
-lower and upper solutions of problem (1.1) and (1.2) such that  on
on  and let
and let  be a Carathéodory function, where
be a Carathéodory function, where

Then, problem (1.1) and (1.2) has at least one solution  such that, for any
such that, for any  ,
,

Proof.
This is a consequence of Theorem 3.5 and Proposition 3.10 and hence, we omits this proof.
4. Singular Case
In this section we give a more general existence result than Theorem 3.11 by assuming the existence of  -lower and upper solutions. This makes us to deal with problem (1.1) and (1.2), where the function
-lower and upper solutions. This makes us to deal with problem (1.1) and (1.2), where the function  is singular at the end point
is singular at the end point  and
and  .
.
Theorem 4.1.
Let  and
and  be
be  -lower and upper solutions of problem (1.1) and (1.2) such that
-lower and upper solutions of problem (1.1) and (1.2) such that  on
on  and let
and let  satisfy the following conditions:
satisfy the following conditions:
(i)for almost every 
 is continuous on
is continuous on  ;
;
(ii)for any  the function
the function  is measurable on
is measurable on  ;
;
(iii)there exists a function  such that, for all
such that, for all  ,
,

where

Then problem (1.1) and (1.2) has at least one solution  such that, for all
such that, for all  ,
,

Proof.
Consider the modified problem (3.3) and (1.2) with respect to the given  and
and  and define
and define  by (3.13). Note that by Lemma 2.2,
by (3.13). Note that by Lemma 2.2,  is well defined. Define
is well defined. Define

where

and  is defined by (3.17). The rest arguments are similar to the proof of Theorem 3.5.
is defined by (3.17). The rest arguments are similar to the proof of Theorem 3.5.
Remark 4.2.
We have similar results of Theorems 3.5–4.1, respectively, for (1.1) equipped with

where  is a constant and
is a constant and  ,
,  are given as (1.2).
are given as (1.2).
Example 4.3.
Consider the problem (4.7), for  ,
,  ,
,  ,
,

Clearly,  is a
is a  -lower solution of (4.7) and
-lower solution of (4.7) and

where

From Lemma 2.1, we have  and define
and define  . Since, for
. Since, for  ,
, 

that is,  , we have, from Lemma 2.2,
, we have, from Lemma 2.2,  and
and  exists. Let
exists. Let

and, by Lemma 2.2 again, choose  such that
such that

Note that according to the direct computation, we see that  is well-defined and is bounded by
is well-defined and is bounded by  . Next, let
. Next, let  . By Young's inequality, it follows that
. By Young's inequality, it follows that

Hence, such  is a
is a  -upper solution of (4.7) and
-upper solution of (4.7) and  on
on  . Clearly,
. Clearly,  satisfies (i), (ii) of Theorem 4.1. By using Young's inequality again, for
satisfies (i), (ii) of Theorem 4.1. By using Young's inequality again, for  , we have
, we have

and  . Therefore,
. Therefore,  satisfies the assumption (iii) of Theorem 4.1. Consequently, we conclude that this problem has at least one solution
satisfies the assumption (iii) of Theorem 4.1. Consequently, we conclude that this problem has at least one solution  such that, for all
such that, for all  ,
,

Notice that in Theorem 4.1, one can only deal with the case that  is singular at end points
is singular at end points  ,
,  . However, when
. However, when  is singular at
is singular at  , there is no hope to obtain the solutions directly from Theorem 4.1. We will establish the following theorem to deal with this case by constructing upper and lower solutions to solve this problem.
, there is no hope to obtain the solutions directly from Theorem 4.1. We will establish the following theorem to deal with this case by constructing upper and lower solutions to solve this problem.
Theorem 4.4.
Assume
the function  is continuous;
is continuous;
there exists  and for any compact set
and for any compact set  , there is
, there is  such that
such that

for some  and
and  , there is
, there is  such that
such that

where  is defined as in Lemma 2.1.
is defined as in Lemma 2.1.
for any compact set  , there is
, there is  such that
such that

Then problem (1.1) and (1.2) with  has at least one solution
has at least one solution

Remark 4.5 (see [12, Remark  ]).
]).
Assumption  is equivalent to the assumption that there exists
is equivalent to the assumption that there exists  and a function
and a function  such that:
such that:
(i) for all
for all  ,
,
(ii) , for all
, for all  ,
,  ,
,
(iii) , for all
, for all  ,
,
where

Proof.
Step 1.
Construction of lower solutions. Consider  such that
such that  and the function
and the function

where  is chosen small enough so that
is chosen small enough so that

Next, we choose  from the Remark 4.5, and let
from the Remark 4.5, and let

where  is small enough so that for some points
is small enough so that for some points  ,
,  , we have:
, we have:


Notice that by (4.24) and (4.25), for any  such that
such that

we have:


Step 2.
Approximation problems. We define for each  ,
,  ,
,

and set

We have that, for each index  ,
,  is continuous and
is continuous and

where

Hence, the sequence of functions  converges to
converges to  uniformly on any set
uniformly on any set  , where
, where  is an arbitrary compact subset of
is an arbitrary compact subset of  . Next we define
. Next we define

Each of the functions  is a continuous function defined on
is a continuous function defined on  , moreover
, moreover

and the sequence  converges to
converges to  uniformly on the compact subsets of
uniformly on the compact subsets of  since
since

Define now a decreasing sequence  such that
such that

and consider a sequence of the following approximation problems:

where  .
.
Step 3.
A lower solution of ( ). It is clear that for any  ,
,

As the sequence  is decreasing, we also have
is decreasing, we also have

Clearly,  satisfies
satisfies

It follows from (4.25) and (4.27) that  is a lower solution of ( ).
is a lower solution of ( ).
Step 4.
Existence of a solution  of (4.7) such that
of (4.7) such that

From assumption  , we can find
, we can find  and
and  such that, for all
such that, for all  ,
,  ,
,

Also, one has

where  is a suitable constant. Hence, we obtain, for such
is a suitable constant. Hence, we obtain, for such  and
and  ,
,

Let  be a constant such that
be a constant such that

Choose  such that
such that

that is,

where  is defined by (2.1). Note that
is defined by (2.1). Note that  is well-defined and
is well-defined and  since
since  . It is easy to see that
. It is easy to see that

So by Remark 4.2, there is a solution  of (4.7) such that
of (4.7) such that

Step 5.
The problem ( ) has at least one solution  such that
such that

Notice that  is an upper solution of ( ), since
is an upper solution of ( ), since

Step 6.
Existence of a solution. Consider the pointwise limit

It is clear that, for any  ,
,

and therefore  on
on  . Let
. Let  be a compact interval. There is an index
be a compact interval. There is an index  such that
such that  for all
for all  and therefore for these
and therefore for these  ,
,

Moreover, we have

By Arzelá-Ascoli theorem it is standard to conclude that  is a solution of problem (1.1) and (1.2) on the interval
is a solution of problem (1.1) and (1.2) on the interval  . Since
. Since  is arbitrary, we find that
is arbitrary, we find that  and for all
and for all  ,
,

Since

it remains only to check the continuity of  at
at  . This can be deduced from the continuity of
. This can be deduced from the continuity of  and the fact that
and the fact that  as
as  .
.
Example 4.6.
Consider the following problem  , for
, for  ,
, ,
,  ,
,

Let  , where
, where  . Obviously,
. Obviously,  satisfies
satisfies  and
and  . Moreover, for any given
. Moreover, for any given  and for any compact set
and for any compact set  , for
, for  small enough, we have
small enough, we have

Hence,  holds. Furthermore, for
holds. Furthermore, for  large enough,
large enough,  , we have, from Young's inequality by choosing
, we have, from Young's inequality by choosing  and
and  ,
,

where  . Hence,
. Hence,  holds. By Theorem 4.4,
holds. By Theorem 4.4,  has at least one solution
has at least one solution

References
Bitsadze AV, Samarskii AA: On some of the simplest generalizations of linear elliptic boundary-value problems. Doklady Akademii Nauk SSSR 1969, 185: 739–740.
Il'in VA, Moiseev EI: Nonlocal boundary value problem of the first kind for a Sturm-Liouville operator in its differential and finite difference aspects. Differential Equations 1987, 23(7):803–810.
Il'in VA, Moiseev EI: Nonlocal boundary value problem of the second kind for a Sturm-Liouville operator. Differential Equations 1987, 23(7):979–987.
Bitsadze AV: On the theory of nonlocal boundary value problems. Soviet Mathematics—Doklady 1984, 30(1):8–10.
Bitsadze AV: On a class of conditionally solvable nonlocal boundary value problems for harmonic functions. Soviet Mathematics—Doklady 1985, 31(1):91–94.
Bitsadze AV, Samarskii AA: On some simple generalizations of linear elliptic boundary problems. Soviet Mathematics—Doklady 1969, 10(2):398–400.
Yao Q: Successive iteration and positive solution for nonlinear second-order three-point boundary value problems. Computers & Mathematics with Applications 2005, 50(3–4):433–444. 10.1016/j.camwa.2005.03.006
Yao Q: On the positive solutions of a second-order three-point boundary value problem with Caratheodory function. Southeast Asian Bulletin of Mathematics 2004, 28(3):577–585.
Gupta CP, Trofimchuk SI: A sharper condition for the solvability of a three-point second order boundary value problem. Journal of Mathematical Analysis and Applications 1997, 205(2):586–597. 10.1006/jmaa.1997.5252
Ma R: Positive solutions of a nonlinear m -point boundary value problem. Computers & Mathematics with Applications 2001, 42(6–7):755–765. 10.1016/S0898-1221(01)00195-X
Thompson HB, Tisdell C: Three-point boundary value problems for second-order, ordinary, differential equations. Mathematical and Computer Modelling 2001, 34(3–4):311–318. 10.1016/S0895-7177(01)00063-2
De Coster C, Habets P: Upper and lower solutions in the theory of ODE boundary value problems: classical and recent results. In Nonlinear Analysis and Boundary Value Problems for Ordinary Differential Equations, CISM Courses and Lectures. Volume 371. Edited by: Zanolin F. Springer, Vienna, Austria; 1993:1–78.
Lü H, O'Regan D, Agarwal RP: Upper and lower solutions for the singular p -Laplacian with sign changing nonlinearities and nonlinear boundary data. Journal of Computational and Applied Mathematics 2005, 181(2):442–466. 10.1016/j.cam.2004.11.037
Du Z, Xue C, Ge W: Multiple solutions for three-point boundary value problem with nonlinear terms depending on the first order derivative. Archiv der Mathematik 2005, 84(4):341–349. 10.1007/s00013-004-1196-7
Khan RA, Webb JRL: Existence of at least three solutions of a second-order three-point boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2006, 64(6):1356–1366. 10.1016/j.na.2005.06.040
Minghe P, Chang SK: The generalized quasilinearization method for second-order threepoint boundary value problems. Nonlinear Analysis. Theory, Methods & Applications 2008, 68(9):2779–2790. 10.1016/j.na.2007.02.025
Qu WB, Zhang ZX, Wu JD: Positive solutions to a singular second order three-point boundary value problem. Applied Mathematics and Mechanics 2002, 23(7):854–866. 10.1007/BF02456982
De Coster C, Habets P: Two-Point Boundary Value Problems: Lower and Upper Solutions. Springer, Berlin, Germany; 1984.
Habets P, Zanolin F: Upper and lower solutions for a generalized Emden-Fowler equation. Journal of Mathematical Analysis and Applications 1994, 181(3):684–700. 10.1006/jmaa.1994.1052
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, SP., Tsai, LY. Existence Results of Three-Point Boundary Value Problems for Second-order Ordinary Differential Equations. Bound Value Probl 2011, 901796 (2011). https://doi.org/10.1155/2011/901796
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/901796
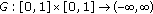 defined by (2.1), is the Green function corresponding for the problem
defined by (2.1), is the Green function corresponding for the problem 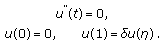
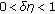 , we have
, we have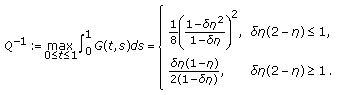
 -Solutions
-Solutions