- Research Article
- Open access
- Published:
Uniqueness results for elliptic problems with singular data
Boundary Value Problems volume 2006, Article number: 98923 (2006)
Abstract
We obtain some uniqueness results for the Dirichlet problem for second-order elliptic equations in an unbounded open set without the cone property, and with data depending on appropriate weight functions. The leading coefficients of the elliptic operator are VMO functions. The hypotheses on the other coefficients involve the weight function.
without the cone property, and with data depending on appropriate weight functions. The leading coefficients of the elliptic operator are VMO functions. The hypotheses on the other coefficients involve the weight function.
References
Adams RA: Sobolev Spaces. Academic Press, New York; 1975:xviii+268.
Caso L: Bounds for elliptic operators in weighted spaces. Journal of Inequalities and Applications 2006, 2006: 14 pages.
Caso L: Regularity results for singular elliptic problems. Journal of Function Spaces and Applications 2006, 4: 17 pages.
Caso L, Cavaliere P, Transirico M: Existence results for elliptic equations. Journal of Mathematical Analysis and Applications 2002,274(2):554–563. 10.1016/S0022-247X(02)00287-1
Caso L, Cavaliere P, Transirico M: Solvability of the Dirichlet problem in
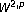 for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche (Catania) 2002,57(2):287–302 (2005).
for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche (Catania) 2002,57(2):287–302 (2005).Caso L, Cavaliere P, Transirico M: Uniqueness results for elliptic equations VMO-coefficients. International Journal of Pure and Applied Mathematics 2004,13(4):499–512.
Caso L, Transirico M: Some remarks on a class of weight functions. Commentationes Mathematicae Universitatis Carolinae 1996,37(3):469–477.
Caso L, Transirico M: The Dirichlet problem for second order elliptic equations with singular data. Acta Mathematica Hungarica 1997,76(1–2):1–16. 10.1007/BF02907048
Cavaliere P, Transirico M, Troisi M: Uniqueness result for elliptic equations in unbounded domains. Le Matematiche (Catania) 1999,54(1):139–146 (2000).
Chiarenza F, Frasca M, Longo P: Interior
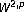 estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149–168.
estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149–168.Chiarenza F, Frasca M, Longo P:
 -solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841–853. 10.2307/2154379
-solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841–853. 10.2307/2154379Chicco M: Solvability of the Dirichlet problem in
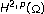 for a class of linear second order elliptic partial differential equations. Bollettino della Unione Matematica Italiana 1971, 4: 374–387.
for a class of linear second order elliptic partial differential equations. Bollettino della Unione Matematica Italiana 1971, 4: 374–387.Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Fundamental Principles of Mathematical Sciences. Volume 224. 2nd edition. Springer, Berlin; 1983:xiii+513.
Greco D: Nuove formole integrali di maggiorazione per le soluzioni di un'equazione lineare di tipo ellittico ed applicazioni alla teoria del potenziale. Ricerche di Matematica 1956, 5: 126–149.
Košelev AI: On boundedness of
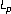 of derivatives of solutions of elliptic differential equations. Matematicheskij Sbornik. Novaya Seriya 1956, 38(80): 359–372.
of derivatives of solutions of elliptic differential equations. Matematicheskij Sbornik. Novaya Seriya 1956, 38(80): 359–372.Miranda C: Sulle equazioni ellittiche del secondo ordine di tipo non variazionale, a coefficienti discontinui. Annali di Matematica Pura ed Applicata. Serie Quarta 1963,63(1):353–386. 10.1007/BF02412185
Pucci C: Limitazioni per soluzioni di equazioni ellittiche. Annali di Matematica Pura ed Applicata. Serie Quarta 1966,74(1):15–30. 10.1007/BF02416445
Transirico M, Troisi M: Second-order nonvariational elliptic equations in unbounded open sets. Annali di Matematica Pura ed Applicata. Serie Quarta 1988, 152: 209–226. 10.1007/BF01766150
Transirico M, Troisi M: Further contributions to the study of second-order elliptic equations in unbounded open sets. Bollettino della Unione Matemàtica Italiana. Serie VII. B 1990,4(3):679–691.
Troisi M: On a class of weight functions. Rendiconti della Accademia Nazionale delle Scienze detta dei XL. Memorie di Matematica e Applicazioni. Serie V. Parte I 1986,10(1):141–152.
Troisi M: On a class of weighted Sobolev spaces. Rendiconti della Accademia Nazionale delle Scienze detta dei XL. Memorie di Matematica e Applicazioni. Serie V. Parte I 1986,10(1):177–189.
Vitanza C: A new contribution to the
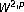 regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche (Catania) 1993,48(2):287–296 (1994).
regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche (Catania) 1993,48(2):287–296 (1994).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Caso, L. Uniqueness results for elliptic problems with singular data. Bound Value Probl 2006, 98923 (2006). https://doi.org/10.1155/BVP/2006/98923
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/98923
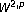 for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche (Catania) 2002,57(2):287–302 (2005).
for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche (Catania) 2002,57(2):287–302 (2005).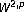 estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149–168.
estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149–168. -solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841–853. 10.2307/2154379
-solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841–853. 10.2307/2154379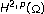 for a class of linear second order elliptic partial differential equations. Bollettino della Unione Matematica Italiana 1971, 4: 374–387.
for a class of linear second order elliptic partial differential equations. Bollettino della Unione Matematica Italiana 1971, 4: 374–387.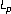 of derivatives of solutions of elliptic differential equations. Matematicheskij Sbornik. Novaya Seriya 1956, 38(80): 359–372.
of derivatives of solutions of elliptic differential equations. Matematicheskij Sbornik. Novaya Seriya 1956, 38(80): 359–372.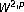 regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche (Catania) 1993,48(2):287–296 (1994).
regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche (Catania) 1993,48(2):287–296 (1994).