- Research
- Open access
- Published:
Bifurcation from interval and positive solutions for a class of fourth-order two-point boundary value problem
Boundary Value Problems volume 2013, Article number: 170 (2013)
Abstract
We consider the fourth-order two-point boundary value problem , , , which is not necessarily linearizable. We give conditions on the parameters k, l and that guarantee the existence of positive solutions. The proof of our main result is based upon topological degree theory and global bifurcation techniques.
MSC:34B15.
1 Introduction
The deformations of an elastic beam in an equilibrium state with fixed both endpoints can be described by the fourth-order boundary value problem
where is continuous, is a parameter and l is a given constant. Since problem (1.1) cannot transform into a system of second-order equations, the treatment method of the second-order system does not apply to it. Thus, the existing literature on problem (1.1) is limited. When , the existence of positive solutions of problem (1.1) has been studied by several authors, see [1–5]. Especially, when , Xu and Han [6] studied the existence of nodal solutions of problem (1.1) by applying disconjugate operator theory and bifurcation techniques.
Recently, motivated by [6], when k, l satisfy (A1), Shen [7] studied the existence of nodal solutions of a general fourth-order boundary value problem by applying disconjugate operator theory [8, 9] and Rabinowitz’s global bifurcation theorem
where
(A1) one of following conditions holds:
-
(i)
k, l satisfying are given constants with
(1.3) -
(ii)
k, l satisfying are given constants with
(1.4)
In this paper, we consider bifurcation from interval and positive solutions for problem (1.2). In order to prove our main result, condition (A1) and the following weaker conditions are satisfied throughout this paper:
(H1) is continuous and there exist functions , , , and such that
for some functions , defined on with
uniformly for , and
for some functions , defined on with
uniformly for .
(H2) for and .
(H3) There exists a function with in any subinterval of such that
It is the purpose of this paper to study the existence of positive solutions of (1.2) under conditions (A1), (H1), (H2) and (H3). The main tool we use is the following global bifurcation theorem for the problem which is not necessarily linearizable.
Theorem A (Rabinowitz [10])
Let V be a real reflexive Banach space. Let be completely continuous such that , . Let () be such that is an isolated solution of the following equation:
for and , where , are not bifurcation points of (1.10). Furthermore, assume that
where is an isolating neighborhood of the trivial solution. Let
Then there exists a continuum (i.e., a closed connected set) 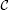 of
of  containing , and either
containing , and either
-
(i)
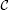 is unbounded in , or
is unbounded in , or -
(ii)
.
Remark 1.1 For other results on the existence and multiplicity of positive solutions and nodal solutions for boundary value problems of fourth-order ordinary differential equations based on bifurcation techniques, see [11–20].
2 Hypotheses and lemmas
Let
Theorem 2.1 (see [[7], Theorem 2.4])
Let (A1) hold. Then
-
(i)
is disconjugate on , and has a factorization
(2.2)
where with ();
-
(ii)
if and only if
(2.3)
where
Theorem 2.2 (see [[7], Theorem 2.7])
Let (A1) hold and with on any subinterval of . Then
-
(i)
the problem
(2.5)
has an infinite sequence of positive eigenvalues
-
(ii)
as ;
-
(iii)
to each eigenvalue , there corresponds an essential unique eigenfunction which has exactly simple zeros in and is positive near 0;
-
(iv)
given an arbitrary subinterval of , an eigenfunction that belongs to a sufficiently large eigenvalue changes its sign in that subinterval;
-
(v)
for each , the algebraic multiplicity of is 1.
Theorem 2.3 (see [[7], Theorem 2.8]) (Maximum principle)
Let (A1) hold. Let with on and in . If satisfies
then on .
Let with the norm . Let with its usual norm . By a positive solution of (1.2), we mean x is a solution of (1.2) with (i.e., in and ).
Let with the inner product and the norm . Further, define the linear operator
with
Then is a closed operator and is completely continuous.
Lemma 2.4 Let be the first eigenfunction of (2.5). Then, for all , we get
Proof Obviously, , we have
Integrating by parts, we obtain
□
Let be the closure of the set of positive solutions of the problem
We extend the function f to a continuous function defined on by
Then for . For , let x be an arbitrary solution of the problem
Since for , we have for . Thus x is a nonnegative solution of (2.11), and the closure of the set of nontrivial solutions of (2.13) in is exactly Σ.
Let be the Nemytskii operator associated with the function
Then (2.13), with , is equivalent to the operator equation
In the following, we shall apply the Leray-Schauder degree theory, mainly to the mapping ,
For , let , and let denote the degree of on with respect to 0.
Lemma 2.5 Let be a compact interval with . Then there exists a number with the property
Proof Suppose to the contrary that there exist sequences and in , in E, such that for all , then in .
Set . Then and . Now, from condition (H1), we have the following:
and, accordingly,
Let and denote the nonnegative eigenfunctions corresponding to and , respectively. Then we have, from the first inequality in (2.19),
From Lemma 2.4, we have
Since in E, from (1.6) we have
By the fact that , we conclude that in E. Thus,
Combining this and (2.21) and letting in (2.20), we get
and consequently
Similarly, we deduce from the second inequality in (2.19) that
Thus, . This contradicts . □
Corollary 2.6 For and , .
Proof Lemma 2.5, applied to the interval , guarantees the existence of such that for ,
Hence, for any ,
which ends the proof. □
Lemma 2.7 Suppose . Then there exists such that with , ,
where is the nonnegative eigenfunction corresponding to .
Proof We assume to the contrary that there exist and a sequence , with and in E, such that for all . As
and in , it follows that
Notice that has a unique decomposition
where and . Since on and , we have from (2.32) that .
Choose such that
By (H1), there exists such that
Therefore, for , ,
Since , there exists such that
and consequently
Applying Lemma 2.4 and (2.37), it follows that
Thus,
This contradicts (2.33). □
Corollary 2.8 For and , .
Proof Let , where is the number asserted in Lemma 2.7. As is bounded in , there exists such that for all . By Lemma 2.7, one has
Hence
□
Now, using Theorem A, we may prove the following.
Proposition 2.9 is a bifurcation interval from the trivial solution for (2.15). There exists an unbounded component C of a positive solution of (2.15), which meets . Moreover,
Proof For fixed with , let us take that , and . It is easy to check that for , all of the conditions of Theorem A are satisfied. So, there exists a connected component of solutions of (2.15) containing , and either
-
(i)
is unbounded, or
-
(ii)
.
By Lemma 2.5, the case (ii) cannot occur. Thus is unbounded bifurcated from in . Furthermore, we have from Lemma 2.5 that for any closed interval , if , then in E is impossible. So, must be bifurcated from in . □
3 Main results
Theorem 3.1 Let (A1), (H1), (H2), (H3) hold. Assume that either
or
then problem (1.2) has at least one positive solution.
Proof of Theorem 3.1 It is clear that any solution of (2.15) of the form yields a solution x of (1.2). We will show that C crosses the hyperplane in . To do this, it is enough to show that C joins to . Let satisfy
We note that for all since is the only solution of (2.15) for and .
Case 1. .
In this case, we show that
We divide the proof into two steps.
Step 1. We show that is bounded.
Since , . From (H3), we have
Let denote the nonnegative eigenfunction corresponding to .
From (3.4), we have
By Lemma 2.4, we have
Thus
Step 2. We show that C joins to .
From (3.3) and (3.7), we have that . Notice that (2.15) is equivalent to the integral equation
which implies that
We divide both of (3.9) by and set . Since is bounded in E, there exists a subsequence of and , with and on , such that
relabeling if necessary. Thus, (3.9) yields that
which implies that
Let and denote the nonnegative eigenfunction corresponding to and , respectively. Then we have, from the first inequality in (3.12),
From Lemma 2.4, integrating by parts, we obtain that
and consequently
Similarly, we deduce from the second inequality in (3.12) that
Thus
So, C joins to .
Case 2. .
In this case, if is such that
and
then
and, moreover,
Assume that is bounded; applying a similar argument to that used in Step 2 of Case 1, after taking a subsequence and relabeling if necessary, we obtain
Again C joins to and the result follows. □
References
Agarwal RP, Chow YM: Iterative methods for a fourth-order boundary value problem. J. Comput. Appl. Math. 1984, 10(2):203–217. 10.1016/0377-0427(84)90058-X
Ma R, Wu HP: Positive solutions of a fourth-order two-point boundary value problem. Acta Math. Sci., Ser. A 2002, 22(2):244–249.
Yao Q: Positive solutions for eigenvalue problems of fourth-order elastic beam equations. Appl. Math. Lett. 2004, 17(2):237–243. 10.1016/S0893-9659(04)90037-7
Yao Q: Solvability of an elastic beam equation with Caratheodory function. Math. Appl. 2004, 17(3):389–392.
Korman P: Uniqueness and exact multiplicity of solutions for a class of fourth-order semilinear problems. Proc. R. Soc. Edinb. A 2004, 134(1):179–190. 10.1017/S0308210500003140
Xu J, Han XL: Nodal solutions for a fourth-order two-point boundary value problem. Bound. Value Probl. 2010., 2010: Article ID 570932
Shen WG: Existence of nodal solutions of a nonlinear fourth-order two-point boundary value problem. Bound. Value Probl. 2012. 10.1186/1687-2770-2012-31
Elias U:Eigenvalue problems for the equations . J. Differ. Equ. 1978, 29(1):28–57. 10.1016/0022-0396(78)90039-6
Elias U Mathematics and Its Applications 396. In Oscillation Theory of Two-Term Differential Equations. Kluwer Academic, Dordrecht; 1997.
Rabinowitz PH: Some aspects of nonlinear eigenvalue problems. Rocky Mt. J. Math. 1973, 3: 161–202. 10.1216/RMJ-1973-3-2-161
Ma R: Existence of positive solutions of a fourth-order boundary value problem. Appl. Math. Comput. 2005, 168(2):1219–1231. 10.1016/j.amc.2004.10.014
Ma R: Nodal solutions for a fourth-order two-point boundary value problem. J. Math. Anal. Appl. 2006, 314(1):254–265. 10.1016/j.jmaa.2005.03.078
Ma R: Nodal solutions of boundary value problem of fourth-order ordinary differential equations. J. Math. Anal. Appl. 2006, 319(2):424–434. 10.1016/j.jmaa.2005.06.045
Ma R, Thompson B: Nodal solutions for a nonlinear fourth-order eigenvalue problem. Acta Math. Sin. Engl. Ser. 2008, 24(1):27–34. 10.1007/s10114-007-1009-6
Ma R, Xu J: Bifurcation from interval and positive solutions of a fourth-order boundary value problem. Nonlinear Anal., Theory Methods Appl. 2010, 72(1):113–122. 10.1016/j.na.2009.06.061
Bai Z, Wang H: On positive solutions of some nonlinear fourth-order beam equations. J. Math. Anal. Appl. 2006, 270(1):357–368. 10.1016/S0022-247X(02)00071-9
Ma R, Gao CH, Han XL: On linear and nonlinear fourth-order eigenvalue problems with indefinite weight. Nonlinear Anal., Theory Methods Appl. 2011, 74(18):6965–6969. 10.1016/j.na.2011.07.017
Ma R, Gao CH: Nodal solutions of a nonlinear eigenvalue problem of the Euler-Bernoulli equation. J. Math. Anal. Appl. 2012, 387(2):1160–1166. 10.1016/j.jmaa.2011.10.019
Ma R, Chen TL: Existence of positive solutions of fourth-order problems with integral boundary conditions. Bound. Value Probl. 2011., 2011: Article ID 297578
Ma R, Xu L: Existence of positive solutions of a nonlinear fourth-order boundary value problem. Appl. Math. Lett. 2010, 23(5):537–543. 10.1016/j.aml.2010.01.007
Acknowledgements
This work is supported by the NSF of Gansu Province (No. 1114-04).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
WS conceived of the study, and participated in its design and coordination and helped to draft the manuscript. TH drafted the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shen, W., He, T. Bifurcation from interval and positive solutions for a class of fourth-order two-point boundary value problem. Bound Value Probl 2013, 170 (2013). https://doi.org/10.1186/1687-2770-2013-170
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-170