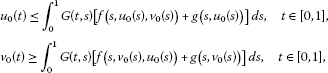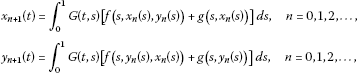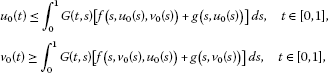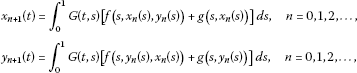- Research
- Open access
- Published:
Mixed monotone operator methods for the existence and uniqueness of positive solutions to Riemann-Liouville fractional differential equation boundary value problems
Boundary Value Problems volume 2013, Article number: 85 (2013)
Abstract
This work is concerned with the existence and uniqueness of positive solutions for the following fractional boundary value problem:
where is the standard Riemann-Liouville fractional derivative of order ν, and , . Our analysis relies on two new fixed point theorems for mixed monotone operators with perturbation. Our results can not only guarantee the existence of a unique positive solution, but also be applied to construct an iterative scheme for approximating it. An example is given to illustrate the main result.
MSC:26A33, 34B18, 34B27.
1 Introduction
In this paper, we investigate the existence and uniqueness of positive solutions for the fractional boundary value problem (FBVP for short) of the form:
where is the standard Riemann-Liouville fractional derivative of order ν, and , .
Fractional differential equations arise in many fields such as physics, mechanics, chemistry, economics, engineering and biological sciences, etc.; see [1–6] for example. In the recent years, there has been a significant development in ordinary and partial differential equations involving fractional derivatives; see the monographs of Miller and Ross [3], Podlubny [5], Kilbas et al. [6], and the papers [7–16] and the references therein. In these papers, many authors have investigated the existence of positive solutions for nonlinear fractional differential equation boundary value problems. On the other hand, the uniqueness of positive solutions for nonlinear fractional differential equation boundary value problems has been studied by some authors; see [10, 14, 17] for example.
In [18], Goodrich utilized the Krasnoselskii’s fixed point theorem to study a FBVP of the form:
and established the existence of at least one positive solution for FBVP (1.2). By using the same fixed point theorem, Goodrich [19] considered the existence of a positive solution to the following systems of differential equations of fractional order:
where , for and , and , with the following boundary value conditions:

under the assumptions that , , f, g are nonnegative and continuous. But the uniqueness of positive solutions is not treated in these papers.
Different from the works mentioned above, motivated by the work [20], we will use two fixed point theorems for mixed monotone operators with perturbation to show the existence and uniqueness of positive solutions for FBVP (1.1). To our knowledge, there are still very few to utilize the fixed point results on mixed monotone operators with perturbation to study the existence and uniqueness of a positive solution for nonlinear fractional differential equation boundary value problems. So, it is worthwhile to investigate FBVP (1.1) by using our new fixed point theorems in [20]. Our results can not only guarantee the existence of a unique positive solution, but also be applied to construct an iterative scheme for approximating it.
With this context in mind, the outline of this paper is as follows. In Section 2 we recall certain results from the theory of fractional calculus and some definitions, notations and results of mixed monotone operators. In Section 3 we provide some conditions, under which the problem FBVP (1.1) has a unique positive solution. Finally, in Section 4, we provide an example, which explicates the applicability of our result.
2 Preliminaries
For the convenience of the reader, we present here some definitions, lemmas and basic results that will be used in the proofs of our theorems.
Definition 2.1 (See [18])
Let with . Suppose that . Then the ν th Riemann-Liouville fractional integral is defined to be
whenever the right-hand side is defined. Similarly, with and , we define the ν th Riemann-Liouville fractional derivative to be
where is the unique positive integer satisfying and .
Lemma 2.2 (See [19])
Let be given. Then the unique solution to problem together with the boundary conditions , where and , is
where
is the Green function for this problem.
Lemma 2.3 (See [19])
Let be as given in the statement of Lemma 2.2. Then we have
-
(i)
is a continuous function on the unit square ;
-
(ii)
for each .
Lemma 2.4 The function defined by (2.2) satisfies the following conditions:
Proof Evidently, the right inequality holds. So, we only need to prove the left inequality. If , then we have , and thus
Hence,
When , we have
So, the proof is complete. □
In the sequel, we present some basic concepts in ordered Banach spaces for completeness and two fixed point theorems which we will be used later. For convenience of readers, we suggest that one refers to [20–22] for details.
Suppose that is a real Banach space which is partially ordered by a cone , i.e., if and only if . If and , then we denote or . By θ we denote the zero element of E. Recall that a non-empty closed convex set is a cone if it satisfies (i) , ; (ii) , .
P is called normal if there exists a constant such that, for all , implies ; in this case, N is called the normality constant of P. If , the set is called the order interval between and . We say that an operator is increasing (decreasing) if implies ().
For all , the notation means that there exist and such that . Clearly, ∼ is an equivalence relation. Given (i.e., and ), we denote by the set . It is easy to see that .
is said to be a mixed monotone operator if is increasing in x and decreasing in y, i.e., , , imply . Element is called a fixed point of A if .
Definition 2.6 An operator is said to be sub-homogeneous if it is satisfies
Definition 2.7 Let and β be a real number with . An operator is said to be β-concave if it satisfies
Lemma 2.8 (See Theorem 2.1 in [20])
Let and . is a mixed monotone operator and satisfies
is an increasing sub-homogeneous operator. Assume that
-
(i)
there is such that and ;
-
(ii)
there exists a constant such that , .
Then:
-
(1)
and ;
-
(2)
there exist and such that
-
(3)
the operator equation has a unique solution in ;
-
(4)
for any initial values , constructing successively the sequences
we have and as .
Lemma 2.9 (See Theorem 2.4 in [20])
Let and . is a mixed monotone operator and satisfies
is an increasing β-concave operator. Assume that
-
(i)
there is such that and ;
-
(ii)
there exists a constant such that , .
Then:
-
(1)
and ;
-
(2)
there exist and such that
-
(3)
the operator equation has a unique solution in ;
-
(4)
for any initial values , constructing successively the sequences
we have and as .
Remark 2.10 (i) If we take in Lemma 2.8, then the corresponding conclusion is still true (see Corollary 2.2 in [20]); (ii) if we take in Lemma 2.9, then the conclusion obtained is also true (see Theorem 2.7 in [23]).
3 Main results
In this section, we apply Lemma 2.8 and Lemma 2.9 to study FBVP (1.1), and we obtain some new results on the existence and uniqueness of positive solutions. The method used here is relatively new to the literature and so are the existence and uniqueness results to the fractional differential equations.
In our considerations, we work in the Banach space with the standard norm . Notice that this space can be equipped with a partial order given by
Set , the standard cone. It is clear that P is a normal cone in and the normality constant is 1.
Theorem 3.1 Assume that
(H1) is continuous and is continuous;
(H2) is increasing in for fixed and , decreasing in for fixed and , and is increasing in for fixed ;
(H3) and for , , , and there exists a constant such that , , , ;
(H4) there exists a constant such that , , .
Then:
-
(1)
there exist and such that and
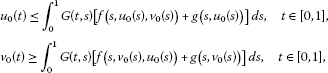
where , and is given as in (2.2);
-
(2)
FBVP (1.1) has a unique positive solution in ;
-
(3)
for any , constructing successively the sequences
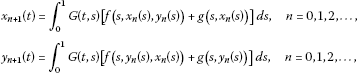
we have and as .
Proof To begin with, from Lemma 2.2, FBVP (1.1) has an integral formulation given by
where is given as in (2.2).
Define two operators and by
It is easy to prove that u is the solution of FBVP (1.1) if and only if . From (H1), we know that and . In the sequel, we check that A, B satisfy all the assumptions of Lemma 2.8.
Firstly, we prove that A is a mixed monotone operator. In fact, for , with , , we know that , , , and by (H2) and Lemma 2.3,
That is, .
Further, it follows from (H2) and Lemma 2.3 that B is increasing. Next we show that A satisfies the condition (2.5). For any and , by (H3) we have
That is, for , . So, the operator A satisfies (2.5). Also, for any , , from (H3) we know that
that is, for , . That is, the operator B is sub-homogeneous. Now we show that and . On the one hand, from (H1), (H2) and Lemma 2.4, for any , we have
On the other hand, also from (H1), (H2) and Lemma 2.4, for any , we obtain
From (H2), (H4), we have
Since , we get
and in consequence,

So, , ; and hence we have . Similarly,
from , we easily prove . Hence the condition (i) of Lemma 2.8 is satisfied.
In the following, we show the condition (ii) of Lemma 2.8 is satisfied. For , and any , from (H4),
Then we get , for . Finally, an application of Lemma 2.8 implies: there exist and such that , ; the operator equation has a unique solution in ; for any initial values , constructing successively the sequences
we have and as . That is,

FBVP (1.1) has a unique positive solution in ; for , the sequences

satisfy and as . □
Theorem 3.2 Assume (H1), (H2) and
(H5) there exists a constant such that , , , , and for , , ;
(H6) for and there exists a constant such that , , .
Then:
-
(1)
there exist and such that and
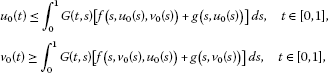
where , and is given as in (2.2);
-
(2)
FBVP (1.1) has a unique positive solution in ;
-
(3)
for any , constructing successively the sequences
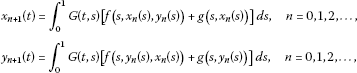
we have and as .
Sketch of the proof Consider two operators A, B defined in the proof of Theorem 3.1. Similarly, from (H1), (H2), we obtain that is a mixed monotone operator and is increasing. From (H5), we have
From (H2), (H6), we have
Since , we get

and in consequence,

So, we can easily prove that , . For , and any , from (H6),
Then we get , for . Finally, an application of Lemma 2.9 implies: there exist and such that , ; the operator equation has a unique solution in ; for any initial values , constructing successively the sequences
we have and as . That is,

FBVP (1.1) has a unique positive solution in ; for , the sequences

satisfy and as . □
From Remark 2.10 and similar to the proofs of Theorems 3.1-3.2, we can prove the following conclusions.
Corollary 3.3 Let . Assume that f satisfies the conditions of Theorem 3.1 and . Then: (i) there exist and such that and

where , and is given as in (2.2); (ii) the FBVP
has a unique positive solution in ; (iii) for any , constructing successively the sequences

we have and as .
Corollary 3.4 Let . Assume that g satisfies the conditions of Theorem 3.2 and for . Then: (i) there exist and such that and
where , and is given as in (2.2); (ii) the FBVP
has a unique positive solution in ; (iii) for any , constructing successively the sequences
we have and as .
4 An example
We now present one example to illustrate Theorem 3.1.
Example 4.1
Consider the following FBVP:
where is a constant, are continuous with .
Obviously, problem (4.1) fits the framework of FBVP (1.1) with , . (Note that , therefore, in this case.) In this example, we take and let

Obviously, ; is continuous and is continuous with . And is increasing in for fixed and , decreasing in for fixed and , and is increasing in for fixed . Besides, for , , , we have

Moreover, if we take , then we obtain
Hence all the conditions of Theorem 3.1 are satisfied. An application of Theorem 3.1 implies that problem (4.1) has a unique positive solution in , where , .
References
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York; 1974.
Gaul L, Klein P, Kempffe S: Damping description involving fractional operators. Mech. Syst. Signal Process. 1991, 5: 81-88. 10.1016/0888-3270(91)90016-X
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York; 1993.
Glockle WG, Nonnenmacher TF: A fractional calculus approach of self-similar protein dynamics. Biophys. J. 1995, 68: 46-53. 10.1016/S0006-3495(95)80157-8
Podlubny I Mathematics in Science and Engineering. In Fractional Differential Equations. Academic Press, New York; 1999.
Kilbas AA, Srivastava HM, Trujillo JJ North-Holland Mathematics Studies 204. In Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam; 2006.
Zhang SQ: Existence of positive solution for some class of nonlinear fractional differential equations. J. Math. Anal. Appl. 2003, 278: 136-148. 10.1016/S0022-247X(02)00583-8
Bai ZB, Lü HS: Positive solutions for boundary value problem of nonlinear fractional differential equation. J. Math. Anal. Appl. 2005, 311: 495-505. 10.1016/j.jmaa.2005.02.052
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Anal. 2008, 69: 3337-3343. 10.1016/j.na.2007.09.025
Zhou Y: Existence and uniqueness of fractional functional differential equations with unbounded delay. Int. J. Dyn. Syst. Differ. Equ. 2008, 1(4):239-244.
Kaufmann ER, Mboumi E: Positive solutions of a boundary value problem for a nonlinear fractional differential equation. Electron. J. Qual. Theory Differ. Equ. 2008., 2008: Article ID 3
Kosmatov N: A singular boundary value problem for nonlinear differential equations of fractional order. J. Appl. Math. Comput. 2009, 29: 125-135. 10.1007/s12190-008-0104-x
Xu X, Jiang D, Yuan C: Multiple positive solutions for boundary value problem of nonlinear fractional differential equation. Nonlinear Anal. 2009, 71: 4676-4688. 10.1016/j.na.2009.03.030
Yang L, Chen H: Unique positive solutions for fractional differential equation boundary value problems. Appl. Math. Lett. 2010, 23: 1095-1098. 10.1016/j.aml.2010.04.042
Wang YQ, Liu LS, Wu YH: Positive solutions for a nonlocal fractional differential equation. Nonlinear Anal. 2011, 74: 3599-3605. 10.1016/j.na.2011.02.043
Lizama C: An operator theoretical approach to a class of fractional order differential equations. Appl. Math. Lett. 2011, 24: 184-190. 10.1016/j.aml.2010.08.042
Yang C, Zhai CB: Uniqueness of positive solutions for a fractional differential equation via a fixed point theorem of a sum operator. Electron. J. Differ. Equ. 2012., 2012: Article ID 70
Goodrich CS: Existence of a positive solution to a class of fractional differential equations. Appl. Math. Lett. 2010, 23: 1050-1055. 10.1016/j.aml.2010.04.035
Goodrich CS: Existence of a positive solution to systems of differential equations of fractional order. Comput. Math. Appl. 2011, 62: 1251-1268. 10.1016/j.camwa.2011.02.039
Zhai CB, Hao MR: Fixed point theorems for mixed monotone operators with perturbation and applications to fractional differential equation boundary value problems. Nonlinear Anal. 2012, 75: 2542-2551. 10.1016/j.na.2011.10.048
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones. Academic Press, Boston; 1988.
Guo D, Lakskmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Anal. 1987, 11(5):623-632. 10.1016/0362-546X(87)90077-0
Zhai CB, Yang C, Zhang XQ: Positive solutions for nonlinear operator equations and several classes of applications. Math. Z. 2010, 266: 43-63. 10.1007/s00209-009-0553-4
Acknowledgements
The authors are grateful to the anonymous referee for his/her valuable suggestions. The first author was supported financially by the Youth Science Foundations of China (11201272) and Shanxi Province (2010021002-1).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhai, C., Hao, M. Mixed monotone operator methods for the existence and uniqueness of positive solutions to Riemann-Liouville fractional differential equation boundary value problems. Bound Value Probl 2013, 85 (2013). https://doi.org/10.1186/1687-2770-2013-85
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-85