- Research
- Open access
- Published:
Existence and multiplicity of solutions for a p-Kirchhoff equation on \({\mathbb {R}}^{N}\)
Boundary Value Problems volume 2018, Article number: 124 (2018)
Abstract
In this paper, we consider the following p-Kirchhoff equation:
where \(f(x,u)=\lambda g(x)|u|^{q-2}u+h(x)|u|^{r-2}u,1< q< p< r< p^{*}\) (\(p^{*}=\frac{Np}{N-p}\) if \(N\ge p,p^{*}=\infty\) if \(N\le p\)). Using variational methods, we prove that, under proper assumptions, there exist \(\lambda_{0},\lambda_{1}>0\) such that problem (P) has a solution for all \(\lambda\in[0,\lambda_{0})\) and has a sequence of solutions for all \(\lambda\in[0,\lambda_{1})\).
1 Introduction and main results
In this paper, we consider the following p-Kirchhoff equation:
where \(M,V\) are continuous functions, \(f(x,u)=\lambda g(x)|u|^{q-2}u+h(x)|u|^{r-2}u\ (1< q< p< r< p^{*})\) is concave and convex, and
Since the pioneering work of Lions [1], much attention has been paid to the existence of nontrivial solutions, multiplicity of solutions, ground state solutions, sign-changing solutions, and concentration of solutions for problem (1.1). For example, for the following Kirchhoff equation:
Li and Ye [2] and Guo [3] showed the existence of a ground state solution for problem (1.2) with \(N=3\), where the potential \(V(x)\in C({\mathbb {R}}^{3})\) and it satisfies \(V(x)\le\liminf_{|y|\to+\infty}V(y)\triangleq V_{\infty}<+\infty\). Sun and Wu [4] investigated the existence and non-existence of nontrivial solutions with the following assumption: \(V(x)\ge0\) and there exists \(c>0\) such that \(\operatorname{meas}\{x\in{\mathbb {R}}^{N}:V(x)< c\}\) is nonempty and has finite measure. Wu [5] proved that problem (1.2) has a nontrivial solution and a sequence of high energy solutions where \(V(x)\) is continuous and satisfies \(\inf V(x) \ge a_{1}>0\) and for each \(M>0\), \(\operatorname{meas}\{x\in{\mathbb {R}}^{N}:V(x)\le M\}<+\infty\). Nie and Wu [6] treated (1.2) where the potential is a radial symmetric function. Chen et al. [7] considered equation (1.2) when \(f(x,u)=\lambda a(x)|u|^{q-2}u+b(x)|u|^{r-2}u\ (1< q< p=2< r<2^{*})\).
Moreover, for p-Kirchhoff-type problem of the following form:
Cheng and Dai [8] proved the existence and non-existence of positive solutions, where \(M(t)\) satisfies
(M) There exists \(\sigma\in(0,1)\) such that \(\hat{M}(t)\ge \sigma[M(t)]t\), here \(\hat{M}(t)=\int_{0}^{t}M(s) \,ds\).
Furthermore, the authors in [9] dealt with problem (1.3) for the special case \(M(t)=t\) and \(p=2\). Recently, Chen and Zhu [10] considered problem (1.3) for \(M(t)=t^{\tau}\) and \(f(u)=|u|^{m-2}u+\mu|u|^{q-2}u\). Similar consideration can be found in [11–13].
However, p-Kirchhoff problem in the following form:
or p-Kirchhoff problem like (1.1) seems to be considered by few researchers as far as we know. Alves et al. [14] and Corrêa and Figueiredo [15] established the existence of a positive solution for problem (1.4) by the mountain pass lemma, where M is assumed to satisfy the following conditions:
- (\(\mathrm{H}_{1}\)):
-
\(M(t)\ge m_{0}\) for all \(t\ge0\).
- (\(\mathrm{H}_{2}\)):
-
\(\hat{M}(t)\ge[M(t)]^{p-1}t\) for all \(t\ge0\), where \(\hat{M}(t)=\int_{0}^{t}[M(s)]^{p-1} \,ds\).
In [16], Liu established the existence of infinitely many solutions to a Kirchhoff-type equation like (1.1). They treated the problem with M satisfying (\(\mathrm{H}_{1}\)) and
- (\(\mathrm{H}_{3}\)):
-
\(M(t)\le m_{1}\) for all \(t>0\).
Very recently, Figueiredo and Nascimento [17] and Santos Junior [18] considered solutions of problem (1.1) by minimization argument and minimax method, respectively, where \(p=2\) and M satisfies (\(\mathrm{H}_{1}\)) and
- (\(\mathrm{H}_{4}\)):
-
The function \(t\mapsto M(t)\) is increasing and the function \(t\mapsto\frac{M(t)}{t}\) is decreasing.
Subsequently, Li et al. [19] investigated the existence, multiplicity, and asymptotic behavior of solutions for problem (1.4), where M could be zero at zero, i.e., the problem is degenerate.
Note that \(M(t)=a+bt\) does not satisfy (\(\mathrm{H}_{2}\)) for \(p=2\) and (\(\mathrm{H}_{3}\)) for all \(1< p< N\). Moreover, \(M(t)=a+bt^{k}\) fails to satisfy (\(\mathrm{H}_{2}\)), (\(\mathrm{H}_{3}\)) for all \(k>0\), and (\(\mathrm{H}_{4}\)) for all \(k>1\). In this paper, we will assume proper conditions on M, which cover the typical case \(M(t)=a+bt^{k}\) and the degenerate case. Furthermore, our assumption on the potential V is totally different from all the previous works which were concerned with Kirchhoff-type problems to the best of our knowledge. The assumption on V is related to the functions \(g,h\) in the nonlinearity f. The potential V is not necessarily radial and can be unbounded or decaying to zero as \(|x|\to+\infty\) according to different functions g and h. See assumptions \((\mathrm{V})\) and (\(\mathrm{M}_{1}\))–(\(\mathrm{M}_{5}\)) below.
Before stating our main results, we introduce some function spaces and then present two embedding theorems, which is important to investigating our problem. For any \(s\in(1,+\infty)\) and any continuous function \(K(x):{\mathbb {R}}^{N}\to{\mathbb {R}},K(x)\ge0,\not \equiv0\), we define the weighted Lebesgue space \(L^{s}({\mathbb {R}}^{N},K)\) equipped with the norm
Throughout the article we assume \(V(x)\) satisfies
- \((\mathrm{V})\) :
-
\(V(x)\in C({\mathbb {R}}^{N})\), \(V(x)\ge0\), and \(\{x\in{\mathbb {R}}^{N}:V(x)=0\}\subset B_{R_{0}}\) for some \(R_{0}>0\), where \(B_{R_{0}}=\{x| |x|\le R_{0},x\in{\mathbb {R}}^{N}\}\).
The natural functional space to study problem (1.1) is X with respect to the norm
The following theorem is due to Lyberopoulos [20]. Denote \(B_{R}=\{ x|x\in{\mathbb {R}}^{N},|x|\le R\}\) and \(B_{R}^{C}={\mathbb {R}}^{N}\backslash B_{R}\).
Theorem 1.1
Let \(p< r< p^{*}\), \(V(x)\) satisfies \((\mathrm{V})\), \(h(x)\in C({\mathbb {R}}^{N})\), and \(h(x)\ge0,\not\equiv0\) such that
where
Then the embedding \(X\hookrightarrow L^{r}({\mathbb {R}}^{N},h)\) is continuous. Furthermore, if \(\mathcal{M}=0\), then the embedding is compact.
Theorem 1.2
Let \(1< q< p\), \(V(x)\) satisfies \((\mathrm{V})\), \(g(x)\in C({\mathbb {R}}^{N})\), \(g(x)\ge0,\not\equiv0\) such that
where
Then the embedding \(X\hookrightarrow L^{q}({\mathbb {R}}^{N},g)\) is continuous. Furthermore, if \(\mathcal{L}=0\), then the embedding is compact.
Proof
This theorem can be seen as a corollary of Theorem 2.3 in [21]. Here we give a detailed proof for the readers convenience. Let \(\varphi_{R}\in C_{0}^{\infty}({\mathbb {R}}^{N})\) be a cut-off function such that \(0\le\varphi_{R}\le1\), \(\varphi_{R}(x)=0\) for \(|x|< R\), \(\varphi_{R}(x)=1\) for \(|x|>R+1\), and \(|D\varphi_{R}(x)|\le C\). For any fixed \(R>R_{0}\), we write \(u=\varphi_{R} u+(1-\varphi_{R})u\). Then it follows from Hölder’s inequality that
Furthermore, by the Sobolev embedding theorem, we have
Combining (1.9) with (1.10), we obtain the continuity of the embedding \(X\hookrightarrow L^{q}({\mathbb {R}}^{N},g)\).
In the following, we prove the embedding \(X\hookrightarrow L^{q}({\mathbb {R}}^{N},g)\) is compact. Let \(\mathcal{L}=0\) and suppose that \(u_{n}\rightharpoonup0\) weakly in X. Then \(\|u_{n}\|_{X}\) is bounded. Hence it follows from (1.9) that for any \(\varepsilon>0\), there exists \(R>0\) sufficiently large such that
Moreover, by the Rellich–Kondrachov theorem, \(\|(1-\varphi_{R}) u_{n}\|_{L^{q}({\mathbb {R}}^{N},g)}\to0\), and so there exists \(n(\epsilon)\in\mathbb{N}\) such that, for all \(n\ge n(\epsilon)\),
Hence, for any \(\epsilon>0\), there exist R and n sufficiently large such that
which implies the embedding \(X\hookrightarrow L^{q}({\mathbb {R}}^{N},g)\) is compact. □
In the rest of the paper, we assume
- \((\mathrm{A})\) :
-
The function V satisfies \((\mathrm{V})\) and the functions \(M,g,h\) are continuous and nonnegative such that \(\mathcal {M}=\mathcal{L}=0\), where \(\mathcal{M}\) and \(\mathcal{L}\) are defined by (1.7) and (1.8), respectively.
By Theorems 1.1 and 1.2, if \(\mathcal{M}=\mathcal{L}=0\), then the embedding \(X\hookrightarrow L^{q}({\mathbb {R}}^{N},g)\) and \(X\hookrightarrow L^{r}({\mathbb {R}}^{N},h)\) is compact for \(1< q< p< r< p^{*}\). Let \(S_{q}\) and \(S_{r}\) be the best embedding constants, then
Since X is a reflexive and separable Banach space, it is well known that there exist \(e_{j}\in X\) and \(e_{j}^{*}\in X^{*}\) \((j=1,2,\ldots)\) such that
-
(1)
\(\langle e_{i},e_{j}^{*}\rangle=\delta_{ij}\), where \(\delta_{ij}=1\) for \(i=j\) and \(\delta_{ij}=0\) for \(i\neq j\).
-
(2)
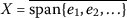 ,
,  .
.
Set
Motivated by [8, 19], we make the following assumptions on M:
- (\(\mathrm{M}_{1}\)):
-
There exists \(\sigma>0\) such that
$$\hat{M}(t)\ge\sigma\bigl[M(t)\bigr]^{p-1}t $$holds for all \(t\ge0\), where \(\hat{M}(t)=\int_{0}^{t}[M(s)]^{p-1} \,ds\).
- (\(\mathrm{M}_{2}\)):
-
\(M(t)\ge m_{0}>0\) for all \(t\ge0\).
- (\(\mathrm{M}_{3}\)):
-
\(M(t)\) is nonnegative and increasing for all \(t\ge0\).
- (\(\mathrm{M}_{4}\)):
-
There exists \(\rho>0\) such that
$$\frac{\sigma}{p}\bigl[M\bigl(\rho^{p}\bigr)\bigr]^{p-1}> \frac{1}{r}S_{r}^{-r/p}\rho^{r-p}, $$where \(S_{r}\) is the best embedding constant of \(X\hookrightarrow L^{r}({\mathbb {R}}^{n},h)\).
- (\(\mathrm{M}_{5}\)):
-
There exists \(\gamma_{1}>0\) such that
$$\frac{\sigma}{p}\bigl[M\bigl(\gamma_{1}^{p}\bigr) \bigr]^{p-1}\gamma_{1}^{p}\ge\frac{\beta _{1}^{r}\gamma_{1}^{r}}{4r}, $$where
$$\beta_{1}=\sup_{u\in Z_{1}, \Vert u \Vert =1} \biggl( \int_{{\mathbb {R}}^{N}}h \vert u \vert ^{r} \,dx \biggr)^{1/r}. $$
The main results of our paper read as follows.
Theorem 1.3
Assume \((\mathrm{A})\), (\(\mathrm{M}_{1}\)) and (\(\mathrm{M}_{2}\)) or (\(\mathrm{M}_{3}\)), (\(\mathrm{M}_{4}\)). Suppose also \(p<\sigma r\) and \(1< q< p< r< p^{*}\). Then there exists \(\lambda_{0}>0\) such that problem (1.1) has a solution for all \(\lambda\in[0,\lambda_{0})\).
Theorem 1.4
Assume \((\mathrm{A})\), (\(\mathrm{M}_{1}\)) and (\(\mathrm{M}_{2}\)) or (\(\mathrm{M}_{3}\)), (\(\mathrm{M}_{4}\)). Suppose also \(p<\sigma r\) and \(1< q< p< r< p^{*}\). Then there exists \(\lambda_{1}>0\) such that problem (1.1) has a sequence \(\{u_{n}\}\) of solutions in X with \(J(u_{n})\to\infty\) as \(n\to\infty\) for all \(\lambda\in[0,\lambda_{1})\).
Remark 1.5
Set \(M(t)=a+bt^{k}\ (a,b,k>0)\). Then we can easily deduce that M satisfies (\(\mathrm{M}_{1}\)) for all \(p>1\) and \(0<\sigma\le\frac{1}{(p-1)k+1}\).
Remark 1.6
Let \(M(t)=a+b\ln(1+t)\ (a,b>0,t\ge0)\). Assume \(p>1,b(p-1)< a\), then by direct calculation, one has
Consequently, M satisfies (\(\mathrm{M}_{1}\)) for \(0<\sigma\le1-\frac{b(p-1)}{a}\).
Remark 1.7
Clearly, assumptions (\(\mathrm{M}_{1}\)), (\(\mathrm{M}_{3}\)), (\(\mathrm{M}_{4}\)) or (\(\mathrm{M}_{1}\)), (\(\mathrm{M}_{3}\)), (\(\mathrm{M}_{5}\)) cover the degenerate case.
2 Proofs of the main results
The associated energy functional to equation (1.1) is
For any \(v\in C_{0}^{\infty}({\mathbb {R}}^{N})\), we have
We say that \(\{u_{n}\}\) is a \((PS)_{c}\) sequence for the functional J if
where \(X^{*}\) denotes the dual space of X. If every \((PS)_{c}\) sequence of J has a strong convergent subsequence, then we say that J satisfies the \((PS)\) condition.
The proof of Theorem 1.3 mainly relies on the following mountain pass lemma in [22] (see also [23]).
Lemma 2.1
Let E be a real Banach space and \(J\in C^{1}(E,\mathbb{R})\) with \(J(0)=0\). Suppose
\((\mathrm{H}_{1})\) there are \(\rho,\alpha>0\) such that \(J(u)\ge\alpha\) for \(\|u\|_{E}=\rho\);
\((\mathrm{H}_{2})\) there is \(e\in E\), \(\|e\|_{E}> \rho\) such that \(J(e)< 0\). Define
Then
is finite and \(J(\cdot)\) possesses a \((PS)_{c}\) sequence at level c. Furthermore, if J satisfies the \((PS)\) condition, then c is a critical value of J.
In the following, we shall verify J satisfies all conditions of the mountain pass lemma.
Lemma 2.2
Assume \((\mathrm{A})\), (\(\mathrm{M}_{1}\)) and (\(\mathrm{M}_{2}\)) or (\(\mathrm{M}_{3}\)). Suppose also \(p<\sigma r\). Then any \((PS)_{c}\) sequence of J is bounded.
Proof
Let \(\{u_{n}\}\) be any \((PS)_{c}\) sequence of J and satisfy (2.3).
By (\(\mathrm{M}_{1}\)) and \((\mathrm{A})\), we have
Case 1. If (\(\mathrm{M}_{2}\)) holds. Then we deduce from (2.4) that
Hence \(\{u_{n}\}\) is bounded.
Case 2. If (\(\mathrm{M}_{3}\)) holds. Let \(\tau_{0}>0\) be fixed. If \(\| u_{n}\|^{p}\ge\tau_{0}\), then
which implies \(\{u_{n}\}\) is bounded. □
Lemma 2.3
Assume \((\mathrm{A})\), (\(\mathrm{M}_{1}\)) and (\(\mathrm{M}_{2}\)) or (\(\mathrm{M}_{4}\)). Then there are \(\rho,\alpha>0\) such that \(J(u)\ge\alpha\) for \(\|u\|=\rho \).
Proof
Case 1. (\(\mathrm{M}_{2}\)) is satisfied. It follows from (1.11), (2.1), and (\(\mathrm{M}_{1}\))–(\(\mathrm{M}_{2}\)) that
Denote \(\phi(t)=At^{p-q}-B\lambda-Ct^{r-q}\) with
Obviously, \(\phi(t)\) attains its maximum
at
Let \(\lambda_{0}=\frac{A(r-p)}{B(r-q)}t_{0}^{p-q}\), \(\rho=t_{0}\), and \(\alpha=t_{0}^{q}\phi(t_{0})\). Then \(J(u)\ge\alpha>0\) for \(\|u\|=\rho\) and \(\lambda\in[0,\lambda_{0})\).
Case 2. (\(\mathrm{M}_{4}\)) is fulfilled. Let \(\|u\|=\rho\). Then, by (1.11), (2.1), and (\(\mathrm{M}_{1}\)), there hold
where \(A(\rho)=\frac{\sigma}{p}[M(\rho^{p})]^{p-1}\) and \(B,C\) is defined by (2.8). In view of (\(\mathrm{M}_{4}\)), \(J(u)\ge\alpha>0\) for all \(0<\lambda<\lambda _{0}=\frac{1}{B}[A(\rho)\rho^{p-q}-C\rho^{r-q}]\). □
Lemma 2.4
Assume \((\mathrm{A})\), (\(\mathrm{M}_{1}\)) and \(p<\sigma r\). Then there is \(e\in X\) with \(\|e\|>\rho\) such that \(J(e)<0\).
Proof
By integrating (\(\mathrm{M}_{1}\)), we obtain
Hence, for \(\|tu\|^{p}\ge t_{1}\),
Consequently, \(J(tu)<0\) if \(t\ge R\) for some \(R>0\) sufficiently large. □
Lemma 2.5
Assume \((\mathrm{A})\), (\(\mathrm{M}_{1}\)) and (\(\mathrm{M}_{2}\)) or (\(\mathrm{M}_{3}\)). Then any \((PS)_{c}\) sequence of J has a strong convergent subsequence.
Proof
Let \(\{u_{n}\}\) be any \((PS)_{c}\) sequence of J and satisfy (2.3). By Lemma 2.2, \(\{u_{n}\}\) is bounded. Passing to a subsequence if necessary, we have
Denote \(P_{n}=\langle J'(u_{n}),u_{n}-u\rangle\) and
We can easily obtain that
Since
we can deduce that
Case 1. (\(\mathrm{M}_{2}\)) holds. Using the standard inequality in \({\mathbb {R}}^{N}\) given by
or
we obtain from (2.12) that \(\|u_{n}-u\|\to0\) as \(n\to\infty\).
Case 2. If (\(\mathrm{M}_{3}\)) holds, then due to the degenerate nature of (1.1), two situations must be considered: either \(\inf_{n}\| u_{n}\|>0\) or \(\inf_{n}\|u_{n}\|=0\).
Case 2-1: \(\inf_{n}\|u_{n}\|>0\). Then we can deduce from (2.12)–(2.14) that \(\|u_{n}-u\|\to0\) as Case 1.
Case 2-2: \(\inf_{n}\|u_{n}\|=0\). If 0 is an accumulation point for the sequence \(\{\|u_{n}\|\}\), then there is a subsequence of \(\{ u_{n}\}\) (not relabelled) such that \(u_{n}\to0\). Hence \(0=J(0)=\lim_{n\to \infty}J(u_{n})= c\). By Lemma 2.3, \(c>0\). This is impossible. Consequently, 0 is an isolated point of \(\{\|u_{n}\|\}\). Therefore, there is a subsequence of \(\{u_{n}\}\) (not relabelled) such that \(\inf_{n}\| u_{n}\|>0\), and we can proceed as before.
This completes the proof. □
Proof of Theorem 1.3
The conclusion follows by Lemmas 2.2–2.5 immediately. □
To get multiplicity result of problem (1.1), we need the following fountain theorem.
Lemma 2.6
(Fountain theorem [24])
Let X be a Banach space with the norm \(\|\cdot\|\), and let \(X_{i}\) be a sequence of subspace of X with \(\dim X_{i}<\infty\) for each \(i\in\mathbb{N}\). Further, set
Consider an even functional \(\Phi\in C^{1}(X,\mathbb{R})\). Assume, for each \(k\in\mathbb{N}\), there exist \(\rho_{k}>\gamma_{k}>0\) such that
- \((\Phi_{1})\) :
-
\(a_{k}:=\max_{u\in Y_{k},\|u\|=\rho_{k}}\Phi(u)\le0\);
- \((\Phi_{2})\) :
-
\(b_{k}:=\inf_{u\in Z_{k},\|u\|=\gamma_{k}}\Phi(u)\to +\infty, k\to+\infty\);
- \((\Phi_{3})\) :
-
Φ satisfies the \((PS)_{c}\) condition for every \(c>0\).
Then Φ has an unbounded sequence of critical values.
Proof of Theorem 1.4
Obviously the functional J is even. It remains to verify that J satisfies \((\Phi_{1})\)–\((\Phi_{3})\) in Lemma 2.6.
It follows from (2.10) that
for positive constants \(C_{1},C_{2}\) and for all \(t\ge0\). Hence
Since all norms are equivalent on the finite dimensional space \(Y_{k}\), we have, for all \(u\in Y_{k}\),
where \(C_{3},C_{4}\) are positive constants. Therefore \(a_{k}:=\max_{u\in Y_{k},\|u\|=\rho_{k}}J(u)<0\) for \(\|u\|=\rho_{k}\) sufficiently large. This gives \((\Phi_{1})\).
Denote \(\beta_{k}=\sup_{u\in Z_{k},\|u\|=1} (\int_{{\mathbb {R}}^{N}}h|u|^{r} \,dx )^{1/r}\). Since \(Z_{k+1}\subset Z_{k}\), we deduce that \(0\le\beta_{k+1}\le\beta_{k}\). Hence \(\beta_{k}\to\beta_{0}\ge0\) as \(k\to+\infty\). By the definition of \(\beta_{k}\), there exists \(u_{k}\in Z_{k}\) with \(\|u_{k}\|=1\) such that
for all \(k\ge1\). Therefore there exists a subsequence of \(\{u_{k}\}\) (not relabelled) such that \(u_{k}\rightharpoonup u\) in X and \(\langle u,e_{j}^{*}\rangle=\lim_{k\to\infty}\langle u_{k},e_{j}^{*}\rangle=0\) for all \(j\ge1\). Consequently, \(u= 0\). This implies \(u_{k}\rightharpoonup0\) in X and so \(u_{k}\to0\) in \(L^{r}({\mathbb {R}}^{N},h)\). Thus \(\beta_{0}=0\). The proof of \((\Phi_{2})\) is divided into the following two cases.
Case 1: (\(\mathrm{M}_{2}\)) holds. For any \(u\in Z_{k}\), there holds
Set
Then
for all \(\lambda\in(0,\lambda_{1})\) and \(\|u\|=\gamma_{k}\). Hence \((\Phi_{2})\) is fulfilled.
Case 2: (\(\mathrm{M}_{3}\)), (\(\mathrm{M}_{5}\)) hold. For \(\|u\|=\rho\), we have
Set
Then by (\(\mathrm{M}_{5}\))
for all \(\lambda\in(0,\widetilde{\lambda}_{1})\) and \(\|u\|=\widetilde {\gamma}_{k}\). Hence \((\Phi_{2})\) is fulfilled.
By Lemma 2.5, we obtain \((\Phi_{3})\). Consequently, the conclusion follows by the fountain theorem. □
References
Lions, J.L.: On some questions in boundary value problems of mathematical physics. In: Contemporary Development in Continuum Mechanics and Partial Differential Equations. North-Holland Math. Stud., vol. 30, pp. 284–346. North-Holland, Amsterdam (1978)
Li, G., Ye, H.: Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in \({\mathbb {R}}^{3}\). J. Differ. Equ. 2014, 257 (2014)
Guo, Z.: Ground states for Kirchhoff equations without compact condition. J. Differ. Equ. 259, 2884–2902 (2014)
Sun, J., Wu, T.: Ground state solutions for an indefinite Kirchhoff type problem with steep potential well. J. Differ. Equ. 256, 1771–1792 (2014)
Wu, X.: Existence of nontrivial solutions and high energy solutions for Schrodinger–Kirchhoff-type equations in \({\mathbb {R}}^{N}\). Nonlinear Anal., Real World Appl. 12, 1278–1287 (2011)
Nie, J., Wu, X.: Existence and multiplicity of non-trivial solutions for Schrodinger–Kirchhoff-type equations with radial potential. Nonlinear Anal. 75, 3470–3479 (2012)
Chen, C., Kuo, Y., Wu, T.: The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions. J. Differ. Equ. 250, 1876–1908 (2011)
Chen, X., Dai, G.: Positive solutions for p-Kirchhoff type problems on \({\mathbb {R}}^{N}\). Math. Methods Appl. Sci. 38, 2650–2662 (2015)
Li, Y., Li, F., Shi, J.: Existence of a positive solution to Kirchhoff type problems without compactness condition. J. Differ. Equ. 253, 2285–2294 (2012)
Chen, C., Zhu, Q.: Existence of positive solutions to p-Kirchhoff-type problem without compactness conditions. Appl. Math. Lett. 28, 82–87 (2014)
Huang, J., Chen, C., Xiu, Z.: Existence and multiplicity results for a p-Kirchhoff equation with a concave-convex term. Appl. Math. Lett. 26, 1070–1075 (2013)
Chen, C., Chen, Q.: Infinitely many solutions for p-Kirchhoff equation with concave-convex nonlinearities in \({\mathbb {R}}^{N}\). Math. Methods Appl. Sci. 39, 1493–1504 (2016)
Santos Junior, J.R., Siciliano, G.: Positive solutions for a Kirchhoff problem with vanishing nonlocal term. J. Differ. Equ. 265, 2034–2043 (2018)
Alves, C.O., Corrêa, F.J.S.A., Ma, T.F.: Positive solutions for a quasilinear elliptic equation of Kirchhoff type. Comput. Math. Appl. 49, 85–93 (2005)
Corrêa, F.J.S.A., Figueiredo, G.M.: On an elliptic equation of p-Kirchhoff type via variational methods. Bull. Aust. Math. Soc. 74(2), 263–277 (2006)
Liu, D.: On a p-Kirchhoff equation via Fountain Theorem and Dual Fountain Theorem. Nonlinear Anal. 72, 302–308 (2010)
Figueiredo, G.M., Nascimento, R.G.: Existence of a nodal solution with minimal energy for a Kirchhoff equation. Math. Nachr. 288(1), 48–60 (2015)
Santos Junior, J.R.: The effect of the domain topology on the number of positive solutions of an elliptic Kirchhoff problem. Nonlinear Anal., Real World Appl. 28, 269–283 (2016)
Li, W., Kun, X., Binlin, Z.: Existence and multiplicity of solutions for critical Kirchhoff-type p-Laplacian problems. J. Math. Anal. Appl. 458, 361–378 (2018)
Lyberopoulos, A.N.: Quasilinear scalar field equations with competing potentials. J. Differ. Equ. 251, 3625–3657 (2011)
Huang, J., Xiu, Z.: Existence and multiplicity of weak solutions for a singular quasilinear elliptic equation. Comput. Math. Appl. 67, 1450–1460 (2014)
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)
Struwe, M.: Variational Methods, Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 3rd edn. Springer, New York (2000)
Willem, M.: Minimax Theorem. Birkhäuser, Boston (1996)
Acknowledgements
The author is grateful to the anonymous referees for their valuable suggestions and comments.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Funding
This work is supported by the Fundamental Research Funds for the Central Universities (2016B07514).
Author information
Authors and Affiliations
Contributions
The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that he has no competing interests regarding the publication of this paper.
Additional information
Abbreviations
No.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, J. Existence and multiplicity of solutions for a p-Kirchhoff equation on \({\mathbb {R}}^{N}\). Bound Value Probl 2018, 124 (2018). https://doi.org/10.1186/s13661-018-1045-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-018-1045-4
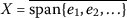 ,
,  .
.