- Research
- Open access
- Published:
Applying periodic and anti-periodic boundary conditions in existence results of fractional differential equations via nonlinear contractive mappings
Boundary Value Problems volume 2023, Article number: 91 (2023)
Abstract
We introduce a notion of nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction and prove related results. With these results, we address the existence and uniqueness results with periodic/anti-periodic boundary conditions for:
1. The nonlinear multi-order fractional differential equation
where
2. The nonlinear multi-term fractional delay differential equation
where
moreover, here \({}^{c}\mathcal{D}^{\delta}\) is predominantly called Caputo fractional derivative of order δ.
1 Introduction
The field of fractional differential equations (FDEs) has gained recognition and significance in recent years as a result of its practical implications with physics, ecology and banking [1, 2]. It is commonly known that classical calculus can be used to model and analyse important and complicated phenomena across many different scientific fields. However, FDEs can provide a deeper examination of many complex natural systems. Diffusion for picture restoration, the spread of viral diseases and other situations fall under this category. In the overwhelming of the aforementioned situations, such types of described anomalous techniques have macroscopically complicated dynamics, and regular derivative frameworks are inadequate to characterise actual behaviour. Therefore, fractional differential equations are preferred over the use of ordinary differential equations [3]. While many conventional methods do not necessarily require explicit mention of fractional differential equations, some research results for fractional differential equations can be attained in a similar manner. As a result, new methods and scientific discoveries are created specifically for fractional differential equations. In light of this, many academicians concentrate on initial and boundary value issues involving various derivative types, such as Atangana–Baleanu, Caputo–Fabrizio and Caputo. The amount of research conducted on the subject has significantly increased over the last few years, with a range of fascinating and useful results (see [4–16]).
The very first statement to the fixed point theory was in a paper proving the existence result. Subsequently, this technique was enhanced as a successive approximating method, and in the context of complete normed space, it was shown and given as a fixed point theorem. It offers a rough technique for precisely characterising the fixed point. It also ensures that a fixed point will exist and be unique. This approach allows us to guarantee that it provides a solution to the initial problem by specifying the conditions that apply when a fixed point resists a particular function. In many different fields of mathematics, the existence result is analogous to the fixed point existence for an applicable function in a variety of mathematical challenges [17–24]. Fixed point results are some of those mathematical notations that show that at least one point still remains fixed when a set’s points are adapted into points of the same set.
Scientific theories of fixed points are very useful in determining whether an equation has a solution. The differential operator, for instance, in differential equations transforms one function into another. It is possible to find the solution of a fractional derivative for a function that has not experienced a substantial progress.
The exponential function \(e^{q}\) is significant to the theory of differential equations with integer orders. Its one-parameter extension, the function that is presently depicted by [25]
was exemplified by Mittag-Leffler in his research articles [26–28].
In particular, Agarwal [29] is credited for the development of the two parameter Mittag-Leffler type function, which is fundamental to the fractional calculus. Humbert and Agarwal [30] explored a variety of correlations for this function by employing the Laplace transform method. The Agarwal function might have been a better name for this function. The two-parameter function is now known as the Mittag-Leffler function, while Humbert and Agarwal cordially left almost the same representation as used for the one-parameter Mittag-Leffler function.
The two-parametric Mittag-Leffler function is defined by (see Podlubny [31])
The Laplace transform for Mittag-Leffler function in two parameters is presented as \(\mathfrak{E}_{j}(a,l; \delta ,\varrho ):=a^{j\delta +\varrho -1} \mathcal{E}_{\delta ,\varrho}^{(j)}(la^{\delta})\) along with the derivatives given by (refer to Podlubny [31])
where \(\mathcal{E}_{\delta ,\varrho}^{(j)}(y)=\frac{d^{j}}{dy^{j}} \mathcal{E}_{\delta ,\varrho}(y)= \sum_{u=0}^{ \infty}\frac{(u+j)!y^{u}}{u!\Gamma (\delta u+\delta j+\varrho )}\), \(j=0,1,2,\ldots\) .
A similar conceptual study can be found in [32] and [33].
The novelty of this article is to explore the connections between fractional Green’s functions, multi-term fractional order differential equations and metric fixed point theory. We prove the existence of a solution and the uniqueness of nonlinear multi-order fractional differential equations via nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction. An interesting feature of our result is that continuity is no longer needed.
2 Nonlinear contractive mappings
Definition 2.1
[34] Let  be a set that is nonempty. Consider
be a set that is nonempty. Consider  . The mapping
. The mapping  is said to be a controlled rectangular metric if the following conditions hold:
is said to be a controlled rectangular metric if the following conditions hold:
-
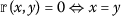 ;
; -
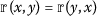 ;
; -
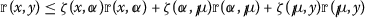
for all  and for all distinct points
and for all distinct points  , each distinct from x and y respectively. As in [34],
, each distinct from x and y respectively. As in [34],  denotes a controlled rectangular metric space (for our convenience, it is called CRMS). The topological properties such as Cauchy, completeness and convergence of controlled rectangular metric space can be seen in [34].
denotes a controlled rectangular metric space (for our convenience, it is called CRMS). The topological properties such as Cauchy, completeness and convergence of controlled rectangular metric space can be seen in [34].
Definition 2.2
[35] \(\mathscr{T}:\mathfrak{B}\cup \mathfrak{C} \rightarrow \mathfrak{B} \cup \mathfrak{C}\) is said to be a cyclic map if \(\mathscr{T}(\mathfrak{B})\subseteq \mathfrak{C}\) and \(\mathscr{T}(\mathfrak{C})\subseteq \mathfrak{B}\), where \(\mathfrak{B}\) and \(\mathfrak{C}\) are nonempty closed subsets of a complete metric space  .
.
Definition 2.3
[36] With respect to a complete metric space, represented by \(\mathcal{X}\), let \(\mathcal{A}\) and \(\mathcal{B}\) be nonempty closed subsets. Using the distance function d and the cyclic mapping \(\mathfrak{H}\), there are some \(k_{x}\in (0, 1)\) such that
Then ς is called a cyclic orbital contraction.
Property-\(\mathcal{F^{\star}}\): Let \(\mathcal{F^{\star}}\) be the family of all functions  and \(\xi :(0,\infty )\rightarrow (0,\infty )\). We say that \(\mathcal{F^{\star}}\) satisfies Property-\(\mathcal{F^{\star}}\) if the following conditions hold:
and \(\xi :(0,\infty )\rightarrow (0,\infty )\). We say that \(\mathcal{F^{\star}}\) satisfies Property-\(\mathcal{F^{\star}}\) if the following conditions hold:
-
\(\mathscr{F}\) is strictly increasing;
-
For every positive sequence
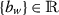 , we have \(\lim_{w\rightarrow \infty}b_{w}=0\) iff \(\lim_{w\rightarrow \infty}\mathscr{F}(b_{w})= -\infty \);
, we have \(\lim_{w\rightarrow \infty}b_{w}=0\) iff \(\lim_{w\rightarrow \infty}\mathscr{F}(b_{w})= -\infty \); -
There exists \(z\in (0,1)\) such that \(\lim_{b\rightarrow 0^{+}}b^{z}\mathscr{F}(b)=0\);
-
\(\lim \inf_{u \rightarrow v^{+}}\xi (u)>0\) for all \(v\geq 0\).
The above-mentioned conditions can be seen in [37] and [38, 39]. In very recent years, Wardowski [37] introduced a novel perspective of contraction and established a fixed point theorem that, in comparison to earlier research findings, generalises the Banach principle of contraction. The conditions mentioned above are a few of the prerequisites that writers must meet in order to formulate statements of specific F-contractions and are also used as key strategies to achieve at fixed point problems (see [40, 41]). The elegance of the \(\mathscr{F}\)-contraction is noteworthy; all that is needed is a complete metric space and an easily verifiable nonlinear condition. The \(\mathscr{F}\)-contraction also has an impact on how conventional methods are modelled. The \(\mathscr{F}\)-contraction continues to be a topic of extra motivation and research due to its broad range of application and usefulness, which constitutes for the emphasis to its generalisations. This illustrates why mathematics has so many implementations in other fields.
We now present our next concept.
Definition 2.4
Suppose that \(\mathfrak{B}\) and \(\mathfrak{C}\) are two nonempty subsets of the CRM-space  and \(\mathcal{F^{\star}}\) is the family of mappings satisfying the property-\(\mathcal{F^{\star}}\). Assume that \(\mathscr{W}\) is a cyclic mapping from \(\mathfrak{B}\cup \mathfrak{C}\) to \(\mathfrak{B}\cup \mathfrak{C}\) such that, for some \(x\in \mathfrak{B}\),
and \(\mathcal{F^{\star}}\) is the family of mappings satisfying the property-\(\mathcal{F^{\star}}\). Assume that \(\mathscr{W}\) is a cyclic mapping from \(\mathfrak{B}\cup \mathfrak{C}\) to \(\mathfrak{B}\cup \mathfrak{C}\) such that, for some \(x\in \mathfrak{B}\),

for all \(w\in \mathbb{N}\) and \(y\in \mathfrak{B}\). Then \(\mathscr{W}\) is called a nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction.
Theorem 2.1
Let  be a controlled rectangular metric space. Suppose that \(\mathfrak{B}\) and \(\mathfrak{C}\) are two nonempty closed subsets of
be a controlled rectangular metric space. Suppose that \(\mathfrak{B}\) and \(\mathfrak{C}\) are two nonempty closed subsets of  . Let \(\mathscr{W}\) be a nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction. For \(x_{0}\in \mathfrak{B}\), take \(x_{w}=\mathscr{W}^{w}x_{0}\). For
. Let \(\mathscr{W}\) be a nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction. For \(x_{0}\in \mathfrak{B}\), take \(x_{w}=\mathscr{W}^{w}x_{0}\). For  , \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x)\), \(\lim_{w \rightarrow +\infty}\zeta (x,x_{w})\) and \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x_{m})\) exist and are finite for all \(w,m\in \mathbb{N}\), \(w\neq m\). Then \(\mathscr{W}\) has a unique fixed point in \(\mathfrak{B}\cap \mathfrak{C}\).
, \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x)\), \(\lim_{w \rightarrow +\infty}\zeta (x,x_{w})\) and \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x_{m})\) exist and are finite for all \(w,m\in \mathbb{N}\), \(w\neq m\). Then \(\mathscr{W}\) has a unique fixed point in \(\mathfrak{B}\cap \mathfrak{C}\).
Proof
Let \(x=x_{0}\in \mathfrak{B}\). Define
Since \(\{x_{0}\}\) in \(\mathfrak{B}\) and \(x_{2w+1}\in \mathfrak{C}\) for \(w\geq 0\).
From (1), we have

This can be written as follows:

Again,

Similarly, we have

By repeating the same process, we get

Since \(\mathscr{F}\) is increasing, then  for all \(w\in \mathbb{N}\), that is, the positive sequence
for all \(w\in \mathbb{N}\), that is, the positive sequence  is decreasing. Therefore it converges to a limit \(r\geq 0\). Inequality (2) becomes
is decreasing. Therefore it converges to a limit \(r\geq 0\). Inequality (2) becomes

Since \(\liminf_{\sigma \rightarrow \theta ^{+}}\xi (\sigma )>0\), we have  . Thus there exist \(w_{0}\in \mathbb{N}\) and \(a>0\) such that, for all \(w\geq w_{0}\),
. Thus there exist \(w_{0}\in \mathbb{N}\) and \(a>0\) such that, for all \(w\geq w_{0}\),  . Hence (3) becomes
. Hence (3) becomes

For all \(w\geq w_{0}\), taking limit as \(n\rightarrow \infty \) in (4), we get

which gives  , and hence condition (2) of property-\(\mathcal{F^{\star}}\),
, and hence condition (2) of property-\(\mathcal{F^{\star}}\),

By using condition (3) of property-\(\mathcal{F^{\star}}\), there exists \(k\in (0,1)\) such that

From (4), we get

and hence,

Taking limit as \(n\rightarrow \infty \), we get

Then there exists \(w_{1}\in \mathbb{N}\) such that, for all \(w\geq w_{1}\),

Now we shall prove that  .
.
For all \(w,m\in \mathbb{N}\), we assume that \(x_{w}\neq x_{m}\). Consider the possibility that \(x_{w}=x_{m}\) in the case of some \(w=m+\gamma \), where \(\gamma >0\), thus \(\mathscr{W}x_{w}=\mathscr{W}x_{m}\).
Consider

Since \(\liminf_{\sigma \rightarrow \theta ^{+}}\xi (\sigma )>0\), we have  .
.
Thus (7) will become

By continuing this process, we get

Therefore, for all \(m,w\in \mathbb{N}\),  .
.
Now we will prove  .
.
In order to this, let us suppose

This can be written as

Again,

This can be written as

By repeating the same process, we get

Since \(\liminf_{\sigma \rightarrow \theta ^{+}}\xi (\sigma )>0\), we have  . Thus there exists \(w_{0}\in \mathbb{N}\) and \(b>0\) such that, for all \(w\geq w_{0}\),
. Thus there exists \(w_{0}\in \mathbb{N}\) and \(b>0\) such that, for all \(w\geq w_{0}\),  . Hence (8) becomes
. Hence (8) becomes

For all \(w\geq w_{0}\), taking limit as \(w\rightarrow \infty \) in (9) and by using condition (2) of property-\(\mathcal{F^{\star}}\), and doing the same process as we did for (4), we get

Now our aim is to prove that \(\{x_{w}\}\) is a Cauchy. In other words, it is represented as

Denote  for all \(p\in \mathbb{N}\). Now split it into two cases.
for all \(p\in \mathbb{N}\). Now split it into two cases.
Case 1: Assume that \(m=w+2\lambda +1\) with \(\lambda \geq 1\). By hypothesis, we have

Thus,

We simply utilise that \(\zeta (x,y)\geq 1\).
Assume
Following that, we are able to express (11) as

Now, let
Since \(0< k<1\), \(\frac{1}{[(\flat -w_{0})a]^{\frac{1}{k}}}\) and \(\frac{1}{[((\flat +1)-w_{0})a]^{\frac{1}{k}}}\) converge, which yields \(a_{\flat}\) converges.
Thus the series
converges.
On the other hand, \(\zeta (x_{w},x_{w+1})\frac{1}{[(w-w_{0})a]^{\frac{1}{k}}}\), \(\zeta (x_{w+1},x_{w+2})\frac{1}{[((w+1)-w_{0})a]^{\frac{1}{k}}}\) converges as \(w\rightarrow \infty \).
From (11), we conclude that  .
.
Case 2: Take \(\rho =2\lambda \) \((\lambda \geq 1)\), thus

Repeating this process and using the hypothesis, we get

Thus we conclude

We simply utilise that \(\zeta (x,y)\geq 1\).
Assume
Then we have

Now let
With the help of (5), we can say that \(b_{\flat}\) converges. Thus the series
converges.
From (10),  converges as \(w\rightarrow \infty \). Thus, from (13), we can write
converges as \(w\rightarrow \infty \). Thus, from (13), we can write

We conclude that the sequence \(x_{w}\) is a Cauchy sequence in the complete controlled rectangular metric space,
which yields \(\mathfrak{B}\cap \mathfrak{C}\neq \emptyset \), as \(\mathscr{W}^{w}x\rightarrow \sigma \), where \(\sigma \in \mathfrak{B}\cap \mathfrak{C}\).
Now we prove \(\mathscr{W}\sigma =\sigma \). From nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction, we have

Applying \(\lim_{w\rightarrow \infty}\) to the above inequality, we get

and hence from the property-\(\mathcal{F^{\star}}\), we have

Finally, we show that σ is a unique fixed point of \(\mathscr{W}\). Suppose on the contrary that there exists a point \(\beta \in \mathfrak{B}\cap \mathfrak{C}\) such that \(\sigma \neq \beta \) and \(\mathscr{W}\beta =\beta \).

which is a contradiction. Hence \(\sigma =\beta \). This completes the proof. □
Theorem 2.2
Let \(\mathfrak{B}\) and \(\mathfrak{C}\) be nonempty subsets of CRMS  with property \(\mathscr{F}^{*}\). Suppose that \(\mathscr{W}\) is a cyclic mapping from \(\mathfrak{B}\cup \mathfrak{C}\) to \(\mathfrak{B}\cup \mathfrak{C}\) such that
with property \(\mathscr{F}^{*}\). Suppose that \(\mathscr{W}\) is a cyclic mapping from \(\mathfrak{B}\cup \mathfrak{C}\) to \(\mathfrak{B}\cup \mathfrak{C}\) such that

Take \(x_{0}\in \mathfrak{B}\) and \(x_{w}=\mathscr{W}^{w}x_{0}\). For  , \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x)\), \(\lim_{w \rightarrow +\infty}\zeta (x,x_{w})\) and \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x_{m})\) exist and are finite. Then there will be a fixed point that is unique in \(\mathfrak{B}\cap \mathfrak{C}\).
, \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x)\), \(\lim_{w \rightarrow +\infty}\zeta (x,x_{w})\) and \(\lim_{w\rightarrow +\infty}\zeta (x_{w},x_{m})\) exist and are finite. Then there will be a fixed point that is unique in \(\mathfrak{B}\cap \mathfrak{C}\).
Proof
Take \(x_{0}\in \mathfrak{B}\cup \mathfrak{C}\). Moreover, define \(x_{w}=\mathscr{W}^{w}x_{0}\). Thus, for \(x_{0}\in \mathfrak{B}\cap \mathfrak{C}\),  ,
,

We can determine that, by induction,

By using the same pattern as in the above theorem, one can prove that \(\{\mathscr{W}^{w}x\}\) converges to some point \(\vartheta \in \mathfrak{B}\cup \mathfrak{C}\). Note that an infinite number of terms of the sequence \(\{\mathscr{W}^{w}x\}\) lie in \(\mathfrak{B}\) and an infinite number of terms lie in \(\mathfrak{C}\). Thus \(\vartheta \in \mathfrak{B}\cap \mathfrak{C}\). So \(\mathfrak{B}\cap \mathfrak{C}\neq \phi \).
Since \(\mathscr{W}\) is cyclic, \(\mathscr{W}(\mathfrak{B})\subseteq \mathfrak{C}\) and \(\mathscr{W}(\mathfrak{C})\subseteq \mathfrak{B}\) lead to \(\mathscr{W}:\mathfrak{B}\cap \mathfrak{C}\rightarrow \mathfrak{B} \cap \mathfrak{C}\). Thus (15) implies that \(\mathscr{W}\) restricted to \(\mathfrak{B}\cap \mathfrak{C}\) is a cyclic \(\mathscr{F}\)-contractive mapping. Hence the defined contractive mapping applies to \(\mathscr{W}\) on \(\mathfrak{B}\cap \mathfrak{C}\). Hence one can easily prove that \(\mathscr{W}\) has a unique fixed point in \(\mathfrak{B}\cap \mathfrak{C}\). □
3 Connecting fixed point elements to nonlinear multi-order fractional differential equations
We utilise our Theorem 2.2 to investigate the existence and uniqueness of solutions for the nonlinear fractional differential equation of multi-order. An interesting feature about our result is that continuity is no longer needed. The nonlinear multi-order fractional differential equation is studied in the current section:
Here,

with the periodic boundary condition
and the anti-periodic boundary condition
Theorem 3.1
Under the following assumptions, boundary value problem (16)–(17) and (16)–(18) has a unique solution.
- \((\mathcal{A}_{1})\).:
-
For all \(\varsigma \in [0,\mathscr{A}]\), we have
$$ \psi (\varsigma )\leq \int _{0}^{\mathscr{A}}\mathscr{G}(\varsigma , \varkappa )\sigma \bigl(\varkappa ,\varphi (\varkappa ) \bigr)\,d \varkappa $$(19)and
$$ \varphi (\varsigma )\geq \int _{0}^{\mathscr{A}}\mathscr{G}( \varsigma ,\varkappa )\sigma \bigl(\varkappa ,\psi (\varkappa ) \bigr)\,d \varkappa . $$(20) - \((\mathcal{A}_{2})\).:
-
For all \(\varkappa \in [0,\mathscr{A}]\), σ is a decreasing function, that is,
 , \(x\geq y\Rightarrow \sigma (\varkappa ,x)\leq \sigma (\varkappa ,y)\).
, \(x\geq y\Rightarrow \sigma (\varkappa ,x)\leq \sigma (\varkappa ,y)\). - \((\mathcal{A}_{3})\).:
-
\(\sup_{\varsigma \in [0,\mathscr{A}]}\int _{0}^{\mathscr{A}} \mathscr{G}(\varsigma ,\varkappa )\,d \varkappa \leq 1\).
- \((\mathcal{A}_{4})\).:
-
For all \(\varkappa \in [0,\mathscr{A}]\), for all
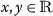 with \((x\leq \varphi _{0} \textit{ and } y\geq \psi _{0})\) or \((x\geq \psi _{0} \textit{ and } y\leq \varphi _{0})\) for
with \((x\leq \varphi _{0} \textit{ and } y\geq \psi _{0})\) or \((x\geq \psi _{0} \textit{ and } y\leq \varphi _{0})\) for 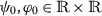 .
. - \((\mathcal{A}_{5})\).:
-
\(|\sigma (\varsigma ,y)-\sigma (\varsigma ,x)|\leq \frac{1}{\tilde{\mathscr{G}}}|y-x|e^{-\frac{1}{|y-x|}}, x\),
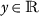 , where \(\tilde{\mathscr{G}}=\sup \{\int _{0}^{\mathscr{A}}|\mathscr{G}( \varsigma ,\varkappa )|\,d \varkappa , \varsigma \in [0,\mathscr{A}]\}\); here the function \(\varsigma \in [0,\mathscr{A}]\mapsto \int _{0}^{\mathscr{A}}| \mathscr{G}(\varsigma ,\varkappa )|\,d \varkappa \) is continuous on \([0,\mathscr{A}]\).
, where \(\tilde{\mathscr{G}}=\sup \{\int _{0}^{\mathscr{A}}|\mathscr{G}( \varsigma ,\varkappa )|\,d \varkappa , \varsigma \in [0,\mathscr{A}]\}\); here the function \(\varsigma \in [0,\mathscr{A}]\mapsto \int _{0}^{\mathscr{A}}| \mathscr{G}(\varsigma ,\varkappa )|\,d \varkappa \) is continuous on \([0,\mathscr{A}]\). - \((\mathcal{A}_{6})\).:
-
The mapping σ from
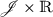 to
to 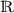 is continuous.
is continuous. - \((\mathcal{A}_{7})\).:
-
Define the set \(\mathcal{C}=\{\theta \in \mathbb{C}([0,\mathscr{A}])/\psi \leq \theta (\varsigma )\leq \varphi \textit{ for all } \varsigma \in [0, \mathscr{A}]\}\).
Proof
Let  represent the set of all continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into
represent the set of all continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into  with the norm
with the norm
 represents the set of all functions characterised on \(\mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0\).
represents the set of all functions characterised on \(\mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0\).
Applying periodic boundary condition:
Case-1: \(w=1\) and \(\psi _{0}=0\).
The nonlinear fractional differential equation (16)–(17) reduces to
\(\varsigma \in \mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0, \gamma _{0}\),  , \(\gamma _{1}\neq 0\), the boundary conditions that are periodic \(\theta (0)=\theta (\mathscr{A})\) yield the equation for the fractional integral
, \(\gamma _{1}\neq 0\), the boundary conditions that are periodic \(\theta (0)=\theta (\mathscr{A})\) yield the equation for the fractional integral
under which \(\mathscr{G}(\varsigma ,\varkappa )\) is the subsequent Green function
Case-2: \(w\geq 2\).
The nonlinear fractional differential equation (16)–(17)
where

the boundary conditions that are periodic
yield the equation for the fractional integral
under which \(\mathscr{G}(\varsigma ,\varkappa )\) is the subsequent Green function:
For \(0\leq \varkappa <\varsigma \),
For \(\varsigma \leq \varkappa <\mathscr{A}\),
where the terms \((r; a_{0},a_{1},a_{2},\ldots,a_{w-2})\) are the so-called the multinomial coefficients; here, moreover,
Applying anti-periodic boundary condition:
Case-1: \(w=1\), \(\delta _{0}=0\).
The nonlinear fractional differential equation (16)–(17) reduces to
\(\varsigma \in \mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0, \gamma _{0}\),  , \(\gamma _{1}\neq 0\), the boundary conditions that are anti-periodic \(\theta (0)=-\theta (\mathscr{A})\) yield the equation for the fractional integral
, \(\gamma _{1}\neq 0\), the boundary conditions that are anti-periodic \(\theta (0)=-\theta (\mathscr{A})\) yield the equation for the fractional integral
under which \(\mathscr{G}(\varsigma ,\varkappa )\) is the subsequent Green function:
Case-2: \(w\geq 2\).
The nonlinear fractional differential equation \(\mathcal{L}(\mathcal{D})\theta (\varsigma )=\sigma (\varsigma , \theta (\varsigma ))\), the boundary conditions that are anti-periodic \(\theta (0)=-\theta (\mathscr{A})\) yield the equation for the fractional integral
under which \(\mathscr{G}(\varsigma ,\varkappa )\) is the subsequent Green function:
For \(0\leq \varkappa <\varsigma \),
For \(\varsigma \leq \varkappa <\mathscr{A}\),
where the terms \((r; a_{0},a_{1},a_{2},\ldots,a_{w-2})\) are the so-called the multinomial coefficients; here, moreover,
Now consider the fractional integral
where (17) and (18) are the boundary conditions and \(\mathscr{G}(\varsigma ,\varkappa )\) is the Green function referring to those ailments accordingly, as given above, and the function  is continuous.
is continuous.
Let  be the set of real-valued continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into
be the set of real-valued continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into  . We endow
. We endow  with
with  for all
for all  .
.
Define  by
by
It is clear that  is a CRMS.
is a CRMS.
Let us define  and \(\xi :(0,\infty )\rightarrow (0,\infty )\) by \(\mathscr{F}(z)=\log z\), \(z>0\) and \(\xi (t)=\frac{1}{t}\),
and \(\xi :(0,\infty )\rightarrow (0,\infty )\) by \(\mathscr{F}(z)=\log z\), \(z>0\) and \(\xi (t)=\frac{1}{t}\),  .
.
Let  ,
,  such that
such that
Define the closed subsets of  , \(\mathfrak{B}\) and \(\mathfrak{C}\) by
, \(\mathfrak{B}\) and \(\mathfrak{C}\) by

Define the mapping  by
by
We shall prove that
Let \(\theta \in \mathfrak{B}\), that is, \(\theta (\varkappa )\leq \varrho (\varkappa )\) for all \(\varkappa \in [0,\mathscr{A}]\). By using \((\mathcal{A}_{2})\) of our assumption, we get
as \(\mathscr{G}(\varsigma ,\varkappa )\geq 0\) for all \(\varsigma ,\varkappa \in [0,\mathscr{A}]\).
The above inequality with hypothesis implies that
Thus \(\mathscr{A}\theta \in \mathfrak{C}\).
Similarly, let \(\theta \in \mathfrak{C}\), that is, \(\theta (\varkappa )\geq \delta (\varkappa )\) for all \(\varkappa \in [0,\mathscr{A}]\). By using \((\mathcal{A}_{2})\) of our assumption and since \(\mathscr{G}(\varsigma ,\varkappa )\geq 0\) for all \(\varsigma ,\varkappa \in [0,\mathscr{A}]\), we get
The above inequality with hypothesis implies that
Thus \(\mathscr{A}\theta \in \mathfrak{B}\).
Hence \(\mathscr{A}(\mathfrak{B})\subseteq \mathfrak{C} \) and \(\mathscr{A}(\mathfrak{C})\subseteq \mathfrak{B}\).
Now, let \(\theta \in \mathfrak{B}\) and \(\mu \in \mathfrak{C}\), that is, for all \(\varsigma \in [0,\mathscr{A}]\),
This implies that for all \(\varsigma \in [0,\mathscr{A}]\),
Now, by using conditions \((\mathcal{A}_{3})\) and \((\mathcal{A}_{5})\),

which implies

Thus,

Applying log on both sides, we get

A similar method can be used to demonstrate that the inequality mentioned above is true if we take \(\theta \in \mathfrak{C}\) and \(\mu \in \mathfrak{B}\). Thus, by our Theorem 2.2, \(\mathscr{A}\) has a unique fixed point, as it satisfied all the conditions of Theorem 2.2. □
We deduce that \(\mathscr{A}\) has a unique fixed point \(\theta ^{*}\in \mathfrak{B}\cap \mathfrak{C}=\mathcal{C}\), that is, \(\theta ^{*}\in \mathcal{C}\) is the unique solution to boundary value problem (16)–(17) and (16)–(18). More importantly, we have utilised our fixed point result to demonstrate the existence of solution to nonlinear multi-order fractional differential equation with boundary conditions that are periodic/anti-periodic in the context of CRMS without considering the property of continuity.
Theorem 3.2
Under the following assumptions, boundary value problem (16)–(17) and (16)–(18) has a unique solution.
- \((\mathcal{C}_{1})\).:
-
For all \(\varsigma \in [0,\mathscr{A}]\), we have
$$ \psi (\varsigma )\leq \int _{0}^{\mathscr{A}}\mathscr{G}(\varsigma , \varkappa )\sigma \bigl(\varkappa ,\varphi (\varkappa ) \bigr)\,d \varkappa $$(27)and
$$ \varphi (\varsigma )\geq \int _{0}^{\mathscr{A}}\mathscr{G}( \varsigma ,\varkappa )\sigma \bigl(\varkappa ,\psi (\varkappa ) \bigr)\,d \varkappa . $$(28) - \((\mathcal{C}_{2})\).:
-
For all \(\varkappa \in [0,\mathscr{A}]\), σ is a decreasing function, that is,
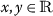 , \(x\geq y\Rightarrow \sigma (\varkappa ,x)\leq \sigma (\varkappa ,y)\).
, \(x\geq y\Rightarrow \sigma (\varkappa ,x)\leq \sigma (\varkappa ,y)\). - \((\mathcal{C}_{3})\).:
-
\(\sup_{\varsigma \in [0,\mathscr{A}]}\int _{0}^{\mathscr{A}} \mathscr{G}(\varsigma ,\varkappa )\,d \varkappa \leq 1\).
- \((\mathcal{C}_{4})\).:
-
For all \(\varkappa \in [0,\mathscr{A}]\), for all
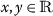 with \((x\leq \varphi _{0} \textit{ and } y\geq \psi _{0})\) or \((x\geq \psi _{0} \textit{ and } y\leq \varphi _{0})\) for
with \((x\leq \varphi _{0} \textit{ and } y\geq \psi _{0})\) or \((x\geq \psi _{0} \textit{ and } y\leq \varphi _{0})\) for 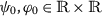 .
. - \((\mathcal{C}_{5})\).:
-
There exists a strictly increasing sequence \((\ell _{w})_{w\in \mathbb{N}\cup \{0\}}\) satisfying \(w_{0}=0\), \(\ell _{w}\geq 1\), \(\ell _{w}-\ell _{w-1}\leq 1\) for all \(w\in \mathbb{N}\), \(\ell _{w}\rightarrow \infty \) such that, for any \(w\in \mathbb{N}\),
$$ \bigl\vert \sigma (\varsigma ,y)-\sigma (\varsigma ,x) \bigr\vert ^{2}\leq \frac{1}{(\tilde{\mathscr{G}})^{2}}\frac{1}{e^{x_{w}-(x_{w-1})^{2}}} \vert y-x \vert ^{2} $$for all
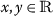 and \(\varsigma \in \mathscr{J}\) such that \(|y-x|< x_{w}e^{\mathscr{A}}\),where \(\tilde{\mathscr{G}}=\sup \{\int _{0}^{\mathscr{A}}|\mathscr{G}( \varsigma ,\varkappa )|\,d \varkappa , \varsigma \in [0,\mathscr{A}]\}\).
and \(\varsigma \in \mathscr{J}\) such that \(|y-x|< x_{w}e^{\mathscr{A}}\),where \(\tilde{\mathscr{G}}=\sup \{\int _{0}^{\mathscr{A}}|\mathscr{G}( \varsigma ,\varkappa )|\,d \varkappa , \varsigma \in [0,\mathscr{A}]\}\). - \((\mathcal{C}_{6})\).:
-
σ is a mapping from
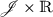 to
to  is continuous.
is continuous. - \((\mathcal{C}_{7})\).:
-
Define the set \(\mathcal{C}=\{\theta \in \mathbb{C}([0,\mathscr{A}])/\psi \leq \theta (\varsigma )\leq \varphi \textit{ for all } \varsigma \in [0, \mathscr{A}]\}\).
Proof
Let  represent the set of all continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into
represent the set of all continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into  with the norm
with the norm
 represents the set of all real-valued functions characterised on \(\mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0\) consisting of continuous derivatives.
represents the set of all real-valued functions characterised on \(\mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0\) consisting of continuous derivatives.
Applying periodic boundary condition:
Case-1: \(w=1\) and \(\psi _{0}=0\).
The nonlinear fractional differential equation (16)–(17) reduces to
\(\varsigma \in \mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0, \gamma _{0}\),  , \(\gamma _{1}\neq 0\), with boundary condition that is periodic \(\theta (0)=\theta (\mathscr{A})\) and is equal to the fractional integral
, \(\gamma _{1}\neq 0\), with boundary condition that is periodic \(\theta (0)=\theta (\mathscr{A})\) and is equal to the fractional integral
The following Green function, where \(\mathscr{G}(\mathfrak{h},\varkappa )\), is used:
Case-2: \(w\geq 2\).
The nonlinear fractional differential equation (16)–(17)
here,

with boundary condition that is periodic
equal to the fractional integral
where \(\mathscr{G}(\varsigma ,\varkappa )\) is the following Green function:
For \(0\leq \varkappa <\varsigma \),
For \(\varsigma \leq \varkappa <\mathscr{A}\),
where the terms \((r; a_{0},a_{1},a_{2},\ldots,a_{w-2})\) are the so-called the multinomial coefficients; here, moreover,
Applying anti-periodic boundary condition:
Case-1: \(w=1\), \(\delta _{0}=0\).
The nonlinear fractional differential equation (16)–(17) reduces to
\(\varsigma \in \mathscr{J}=[0,\mathscr{A}]\), \(\mathscr{A}>0, \gamma _{0}\),  , \(\gamma _{1}\neq 0\), has a boundary condition that is anti-periodic \(\theta (0)=-\theta (\mathscr{A})\) and equivalent to the fractional integral equation
, \(\gamma _{1}\neq 0\), has a boundary condition that is anti-periodic \(\theta (0)=-\theta (\mathscr{A})\) and equivalent to the fractional integral equation
where \(\mathscr{G}(\varsigma ,\varkappa )\) is the following Green function:
Case-2: \(w\geq 2\).
The nonlinear fractional differential equation \(\mathcal{L}(\mathcal{D})\theta (\varsigma )=\sigma (\varsigma , \theta (\varsigma ))\) with the boundary value condition that is anti-periodic \(\theta (0)=-\theta (\mathscr{A})\) is equal to the fractional integral
where \(\mathscr{G}(\varsigma ,\varkappa )\) is the following Green function:
For \(0\leq \varkappa <\varsigma \),
For \(\varsigma \leq \varkappa <\mathscr{A}\),
where the terms \((r; a_{0},a_{1},a_{2},\ldots,a_{w-2})\) are the so-called the multinomial coefficients; here, moreover,
Now assume the fractional integral equation
where \(\mathscr{G}(\varsigma ,\varkappa )\) is the Green function corresponding to the boundary conditions (17) and (18), respectively, as given above, and the function  is continuous.
is continuous.
Let  be the set of real-valued continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into
be the set of real-valued continuous functions from \(\mathscr{J}=[0,\mathscr{A}]\) into  . We endow
. We endow  with the
with the  for all
for all  .
.
Define  by
by
It is clear that  is a CRMS.
is a CRMS.
Let  ,
,  such that
such that
Define the closed subsets of  , \(\mathfrak{B}\) and \(\mathfrak{C}\) by
, \(\mathfrak{B}\) and \(\mathfrak{C}\) by

Define the mapping  by
by
We shall prove that
Let \(\theta \in \mathfrak{B}\), that is, \(\theta (\varkappa )\leq \varrho (\varkappa )\) for all \(\varkappa \in [0,\mathscr{A}]\). By using \((\mathcal{C}_{2})\) of our assumption, we get
as \(\mathscr{G}(\varsigma ,\varkappa )\geq 0\) for all \(\varsigma ,\varkappa \in [0,\mathscr{A}]\).
The above inequality (34) with hypothesis implies that
Thus \(\mathscr{A}\theta \in \mathfrak{C}\).
Similarly, let \(\theta \in \mathfrak{C}\), that is, \(\theta (\varkappa )\geq \delta (\varkappa )\) for all \(\varkappa \in [0,\mathscr{A}]\). By using \((\mathcal{C}_{2})\) of our assumption and since \(\mathscr{G}(\varsigma ,\varkappa )\geq 0\) for all \(\varsigma ,\varkappa \in [0,\mathscr{A}]\), we get
Inequality (35) with hypothesis implies that
Thus \(\mathscr{A}\theta \in \mathfrak{B}\).
Hence we proved (33), that is, \(\mathscr{A}(\mathfrak{B})\subseteq \mathfrak{C} \) and \(\mathscr{A}(\mathfrak{C})\subseteq \mathfrak{B}\).
Now, let \(\theta \in \mathfrak{B}\) and \(\mu \in \mathfrak{C}\), that is, for all \(\varsigma \in [0,\mathscr{A}]\),
This implies from the hypothesis that for all \(\varsigma \in [0,\mathscr{A}]\),
A fixed point of the operator \(\mathscr{A}\) in (32) will be the solution of (16)–(17) and (16)–(18), \(i.e\)., nonlinear multi-order fractional differential equation with periodic/anti-periodic boundary conditions.
Let us define  by \(F(a)=\log a\) for \(a>0\) and \(\xi :(0,\infty )\rightarrow (0,\infty )\) by
by \(F(a)=\log a\) for \(a>0\) and \(\xi :(0,\infty )\rightarrow (0,\infty )\) by
Fix \(w\geq 2\).
For any  such that \(\ell _{w-1}<|\theta (\varsigma )-\mu (\varsigma )|<\ell _{w}\).
such that \(\ell _{w-1}<|\theta (\varsigma )-\mu (\varsigma )|<\ell _{w}\).
By using \((\mathcal{C}_{3})\) and \((\mathcal{C}_{5})\),
Thus,

for all  satisfying \(\ell _{w-1}\leq |\theta -\mu |< \ell _{w}\) when \(w\geq 2\) for \(w=1\).
satisfying \(\ell _{w-1}\leq |\theta -\mu |< \ell _{w}\) when \(w\geq 2\) for \(w=1\).
One can easily prove as above that (36) is satisfied for all  such that \(0<|\theta -\mu |<\ell _{1}\).
such that \(0<|\theta -\mu |<\ell _{1}\).
Thus all the conditions of Theorem 2.2 are satisfied. Hence \(\mathscr{A}\) has a unique solution, i.e., nonlinear multi-order differential equation with periodic/anti-periodic boundary conditions has a unique solution. □
4 Connecting fixed point elements to nonlinear multi-term fractional delay differential equations
In this section our Theorem 2.2 is used to investigate the existence and uniqueness of solutions for the nonlinear multi-term fractional delay differential equations:
Here,

and \({}^{c}\mathcal{D}^{\delta}\) denotes the Caputo fractional derivative of order δ. Moreover,  and
and  are continuous with the periodic boundary condition
are continuous with the periodic boundary condition
and the anti-periodic boundary condition
Problem (37)–(38) is equivalent to the integral equations for \(w=1\) and \(\delta _{0}=0\) as well as \(w\geq 2\).
The Green function for problem (37)–(38) when \(w=1\) and \(\delta _{0}=0\) is
The Green function for problem (37)–(38) when \(w\geq 2\) is, for \(0\leq \varkappa <\varsigma \),
For \(\varsigma \leq \varkappa <\mathscr{A}\),
where \((r; a_{0},a_{1},a_{2},\ldots,a_{w-2})= \frac{r!}{a_{0}!,a_{1}!,a_{2}!,\ldots,a_{w-2}!}\) are the so-called the multinomial coefficients; here, moreover,
Problem (37)–(39) is equivalent to the integral equation for \(w=1\) and \(\delta _{0}=0\) as well as for \(w\geq 2\).
where
The Green function for problem (37)–(39) when \(w\geq 2\) is, for \(0\leq \varkappa <\varsigma \),
For \(\varsigma \leq \varkappa <\mathscr{A}\),
where the terms \((r; a_{0},a_{1},a_{2},\ldots,a_{w-2})= \frac{r!}{a_{0}!,a_{1}!,a_{2}!,\ldots,a_{w-2}!}\) are the so-called multinomial coefficients; here, moreover,
Theorem 4.1
Under the following assumptions, boundary value problem (37)–(38) and (37)–(39) has a unique solution.
- \((\mathcal{D}_{1})\).:
-
Let \(\tilde{\mathscr{G}}=\sup \{\int _{0}^{\mathscr{A}}|\mathscr{G}( \varsigma ,\varkappa )|\,d \varkappa , \varsigma \in [0,\mathscr{A}]\}\), where the function \(\varsigma \in [0,\mathscr{A}]\mapsto \int _{0}^{\mathscr{A}}| \mathscr{G}(\varsigma ,\varkappa )|\,d \varkappa \) is continuous on \([0,\mathscr{A}]\).
- \((\mathcal{D}_{2})\).:
-
Define the set \(\mathcal{C}=\{\theta \in \mathbb{C}([-\tau ,\mathscr{A}])/\psi \leq \theta (\varsigma )\leq \varphi \textit{ for all } \varsigma \in [- \tau ,\mathscr{A}]\}\).
- \((\mathcal{D}_{3})\).:
-
The function
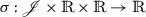 is continuous.
is continuous. - \((\mathcal{D}_{4})\).:
-
For all \(\varsigma \in [0,\mathscr{A}]\), we have
$$ \psi (\varsigma )\leq \int _{0}^{\mathscr{A}}\mathscr{G}(\varsigma , \varkappa )\sigma \bigl(\varkappa ,\varphi (\varkappa ),\varphi ( \varkappa -\tau ) \bigr) \,d \varkappa $$(40)and
$$ \varphi (\varsigma )\geq \int _{0}^{\mathscr{A}}\mathscr{G}( \varsigma ,\varkappa )\sigma \bigl(\varkappa ,\psi (\varkappa ),\psi ( \varkappa -\tau ) \bigr)\,d \varkappa . $$(41) - \((\mathcal{D}_{5})\).:
-
For all \(\varkappa \in [0,\mathscr{A}]\), σ is a decreasing function, that is,
 , \(x\geq y\Rightarrow \sigma (\varkappa ,x)\leq \sigma (\varkappa ,y)\).
, \(x\geq y\Rightarrow \sigma (\varkappa ,x)\leq \sigma (\varkappa ,y)\). - \((\mathcal{D}_{6})\).:
-
\(\sup_{\varsigma \in [0,\mathscr{A}]}\int _{0}^{\mathscr{A}} \mathscr{G}(\varsigma ,\varkappa )\,d \varkappa \leq 1\).
- \((\mathcal{D}_{7})\).:
-
For all \(\varkappa \in [0,\mathscr{A}]\), for all
 with \((x\leq \varphi _{0} \textit{ and } y\geq \psi _{0})\) or \((x\geq \psi _{0} \textit{ and } y\leq \varphi _{0})\) for
with \((x\leq \varphi _{0} \textit{ and } y\geq \psi _{0})\) or \((x\geq \psi _{0} \textit{ and } y\leq \varphi _{0})\) for 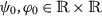 .
. - \((\mathcal{D}_{8})\).:
-
Assume that \(|\sigma (\varsigma ,x_{1},y)-\sigma (\varsigma ,x_{2},y)|\leq |x_{1}-x_{2}|e^{ \frac{1}{|x_{1}-x_{2}|}}\frac{1}{\tilde{\mathscr{G}}}\).
Proof
Let  denote the set of all continuous functions defined on \([-\tau ,\mathscr{A}]\) into
denote the set of all continuous functions defined on \([-\tau ,\mathscr{A}]\) into  with the norm \(\|\theta \|_{\infty}=\sup \{|\theta (\varsigma )|^{2}/\varsigma \in [- \tau ,\mathscr{A}]\}\), \(\mathscr{A}>0\).
with the norm \(\|\theta \|_{\infty}=\sup \{|\theta (\varsigma )|^{2}/\varsigma \in [- \tau ,\mathscr{A}]\}\), \(\mathscr{A}>0\).
Here,  .
.
Let  , we endow
, we endow  with
with

Define  by
by
It is clear that  is a CRMS. Let us define
is a CRMS. Let us define  and
and  by \(\mathscr{F}(s)=\log s\), \(s>0\) and \(\xi (z)=\frac{1}{z}\),
by \(\mathscr{F}(s)=\log s\), \(s>0\) and \(\xi (z)=\frac{1}{z}\),  .
.
Let  ,
,  such that
such that
Define the closed subsets of  , \(\mathfrak{B}\) and \(\mathfrak{C}\) by
, \(\mathfrak{B}\) and \(\mathfrak{C}\) by

Define the operator  as
as
where \(\mathscr{G}(\varsigma ,\varkappa )\) is the Green function of the corresponding boundary value problem.
We shall prove that
Let \(\theta \in \mathfrak{B}\), that is, \(\theta (\varkappa )\leq \varrho (\varkappa )\) for all \(\varkappa \in [0,\mathscr{A}]\). By using \((\mathcal{D}_{2})\) of our assumption, we get
as \(\mathscr{G}(\varsigma ,\varkappa )\geq 0\) for all \(\varsigma ,\varkappa \in [0,\mathscr{A}]\).
The above inequality with hypothesis implies that
Thus \(\mathscr{A}\theta \in \mathfrak{C}\).
Similarly, let \(\theta \in \mathfrak{C}\), that is, \(\theta (\varkappa )\geq \delta (\varkappa )\) for all \(\varkappa \in [0,\mathscr{A}]\). By using \((\mathcal{D}_{2})\) of our assumption and since \(\mathscr{G}(\varsigma ,\varkappa )\geq 0\) for all \(\varsigma ,\varkappa \in [0,\mathscr{A}]\), we get
The above inequality with hypothesis implies that
Thus \(\mathscr{A}\theta \in \mathfrak{B}\).
Hence \(\mathscr{A}(\mathfrak{B})\subseteq \mathfrak{C}\) and \(\mathscr{A}(\mathfrak{C})\subseteq \mathfrak{B}\).
Now, let \(\theta \in \mathfrak{B}\) and \(\mu \in \mathfrak{C}\), that is, for all \(\varsigma \in [0,\mathscr{A}]\),
This implies that for all \(\varsigma \in [0,\mathscr{A}]\),
Let \(\theta (\varsigma )\in \mathfrak{B}\) and \(\mu (\varsigma )\in \mathfrak{C}\).
By using conditions \((\mathcal{D}_{6})\) and \((\mathcal{D}_{8})\),

which implies

Applying log on both sides, we get

Using the same technique, we can show that the above inequality holds also if we take \(\theta \in \mathfrak{C}\) and \(\mu \in \mathfrak{B}\).
Hence \(\mathscr{A}\) has a unique fixed point \(\theta ^{*}\in \mathfrak{B}\cap \mathfrak{C}=\mathcal{C}\), \(i.e.,\theta ^{*}\in \mathcal{C}\) is the unique solution to (37)–(38) and (37)–(39). □
5 Conclusion
In this article, we developed connections between a number of concepts, including Green’s functions, multi-term fractional order differential equations and metric fixed point theory. We provided the results of fixed point of nonlinear cyclic orbital \((\xi -\mathscr{F})\)-contraction under controlled rectangular metric space. With the aid of these results, we were able to derive the existence and uniqueness theorems for fractional boundary value problems in terms of Green’s function for various multi-order fractional differential equations. We shall attempt to use the techniques described in this article in further work, which may serve as some kind of inspiration for using fixed point theory and fractional calculus in neural network algorithms and machine learning systems.
Availability of data and materials
Not applicable.
References
Kochubei, A.N., Luchko, Y.F., Tarasov, V.E., Petras, I.: Handbook of Fractional Calculus with Applications: Applications in Physics. Part A. de Gruyter, Berlin (2019)
Kochubei, A.N., Luchko, Y.F., Tarasov, V.E., Petras, I.: Handbook of Fractional Calculus with Applications: Applications in Physics. Part B. de Gruyter, Berlin (2019)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Atangana, A., Baleanu, D.: New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016). https://doi.org/10.2298/TSCI160111018A
Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 1–13 (2015)
Panda, S.K., Ravichandran, C., Hazarika, B.: Results on system of Atangana–Baleanu fractional order Willis aneurysm and nonlinear singularly perturbed boundary value problems. Chaos Solitons Fractals 142, 110390 (2021). https://doi.org/10.1016/j.chaos.2020.110390
Borah, M.J., Hazarika, B., Panda, S.K., Nieto, J.J.: Examining the correlation between the weather conditions and COVID-19 pandemic in India: a mathematical evidence. Results Phys. 19, 103587 (2020). https://doi.org/10.1016/j.rinp.2020.103587
Kumari, P.S., Panthi, D.: Cyclic compatible contraction and related fixed point theorems. Fixed Point Theory Appl. 2016, 28 (2016). https://doi.org/10.1186/s13663-016-0521-8
Panda, S.K., Kalla, K.S., Nagy, A.M., Priyanka, L.: Numerical simulations and complex valued fractional order neural networks via \((\varepsilon -\mu )\)-uniformly contractive mappings. Chaos Solitons Fractals 173, 113738 (2023). https://doi.org/10.1016/j.chaos.2023.113738
Alqahtani, B., Fulga, A., Karapinar, E., Kumari, P.S.: Sehgal type contractions on dislocated spaces. Mathematics 7(2), 153 (2019). https://doi.org/10.3390/math7020153
Das, A., Hazarika, B., Panda, S.K., et al.: An existence result for an infinite system of implicit fractional integral equations via generalized Darbo’s fixed point theorem. Comput. Appl. Math. 40, 143 (2021). https://doi.org/10.1007/s40314-021-01537-z
Das, A., Rabbani, M., Hazarika, B., Panda, S.K.: A fixed point theorem using condensing operators and its applications to Erdelyi–Kober bivariate fractional integral equations. Turk. J. Math. 46(6), 2513–2529 (2022). https://doi.org/10.55730/1300-0098.3284
Panda, S.K., Vijayakumar, V.: Results on finite time stability of various fractional order systems. Chaos Solitons Fractals 174, 113906 (2023). https://doi.org/10.1016/j.chaos.2023.113906
Gao, W., Baskonus, H.M.: Deeper investigation of modified epidemiological computer virus model containing the Caputo operator. Chaos Solitons Fractals 158, 112050 (2022)
Ilhan, E., Veeresha, P., Baskonus, H.M.: Fractional approach for a mathematical model of atmospheric dynamics of \(\mathrm{CO}_{2}\) gas with an efficient method. Chaos Solitons Fractals 152, 111347 (2021)
Ma, Y.-K., Williams, K., Vijayakumar, V., Nisar, K.S., Shukla, A.: Results on Atangana–Baleanu fractional semilinear neutral delay integro-differential systems in Banach space. J. King Saud Univ., Sci. 34(6), 102158 (2022)
Panda, S.K.: Applying fixed point methods and fractional operators in the modelling of novel coronavirus 2019-nCoV/SARS-CoV-2. Results Phys. 19, 103433 (2020). https://doi.org/10.1016/j.rinp.2020.103433
Panda, S.K., Atangana, A., Nieto, J.J.: New insights on novel coronavirus 2019-nCoV/SARS-CoV-2 modelling in the aspect of fractional derivatives and fixed points. Math. Biosci. Eng. 18(6), 8683–8726 (2021). https://doi.org/10.3934/mbe.2021430
Panda, S.K., Abdeljawad, T., Jarad, F.: Chaotic attractors and fixed point methods in piecewise fractional derivatives and multi-term fractional delay differential equations. Results Phys. 46, 106313 (2023). https://doi.org/10.1016/j.rinp.2023.106313
Hammad, H.A., Aydi, H., De la Sen, M.: Graphical structure of double controlled metric-like spaces with an application. Adv. Cont. Discr. Mod. 2022(1), 1–16 (2022)
Mehmood, M., Shoaib, A., Mlaiki, N.: Fixed point results on triple controlled quasi rectangular metric like spaces. AIMS Math. 8(5), 10049–10066 (2023). https://doi.org/10.3934/math.2023509
Shoaib, A., Rasham, T., Marino, G., Lee, J.R., Park, C.: Fixed point results for dominated mappings in rectangular b-metric spaces with applications. AIMS Math. 5(5), 5221–5229 (2020). https://doi.org/10.3934/math.2020335
Rasham, T., Marino, G., Shoaib, A.: Fixed points for a pair of F-dominated contractive mappings in rectangular b-metric spaces with graph. Mathematics 7(10), 884 (2019). https://doi.org/10.3390/math7100884
Nazam, M., Aydi, H., Hussain, A.: Existence theorems for \((\psi ,\phi )\)-orthogonal interpolative contractions and an application to fractional differential equations. Optimization 72, 1899–1929 (2023)
Erdelyi, A. (ed.): Higher Transcendental Functions, vol. 3. McGraw-Hill, New York (1955)
Mittag-LefIter, G.M.: Sur la nouvelte fonction \(\mathcal{E}_{\alpha}(x)\). C. R. Acad. Sci. Paris 137, 554–558 (1903)
Mittag-Lefller, G.M.: Sopra la funzione \(\mathcal{E}_{\alpha}(x)\). R. Accad. Lincei, Ser. 5 13, 1–35 (1904)
Mittag-Leffler, G.M.: Sur la representation analytique d’une branche uniforme d’une fonction monogene. Acta Math. 29, 101–182 (1905)
Agarwal, R.P.: A propos d’une note de M. Pierre Humbert. C. R. Sdances Acad. Sci. 236(21), 2031–2032 (1953)
Humbert, P., Agarwal, R.P.: Sur la fonction de Mittag-Leffler et quelques-unes de ses generalisations. Bull. Sci. Math. 77(10), 180–185 (1953)
Podlubny, I.: Fractional Differential Equations. Academic Press, Boston (1999)
Choudhary, S., Daftardar-Gejji, V.: Existence uniqueness theorems for multi-term fractional delay differential equations. Fract. Calc. Appl. Anal. 18, 1113–1127 (2015). https://doi.org/10.1515/fca-2015-0064
Choudhary, S., Daftardar-Gejji, V.: Nonlinear multi-order fractional differential equations with periodic/anti-periodic boundary conditions. Fract. Calc. Appl. Anal. 17, 333–347 (2014)
Zubair, S.T., et al.: Controlled b-Branciari metric type spaces and related fixed point theorems with applications. Filomat 34(13), 4253–4269 (2020)
Kirk, W.A., Srinavasan, P.S., Veeramani, P.: Fixed points for mapping satisfying cyclical contractive conditions. Fixed Point Theory 4, 79–89 (2003)
Karpagam, S., Agrawal, S.: Best proximity points theorems for cyclic Meir–Keeler contraction maps. Nonlinear Anal. 74, 1040–1046 (2011)
Wardowski, D.: Solving existence problems via F-contractions. Proc. Am. Math. Soc. 146(4), 1585–1598 (2018)
Piri, H., Kumam, P.: Some fixed point theorems concerning F-contraction in complete metric spaces. Fixed Point Theory Appl. 2014, 210 (2014). https://doi.org/10.1186/1687-1812-2014-210
Wardowski, D.: Fixed point theory of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 94 (2012)
Minak, G., Halvaci, A., Altun, I.: Ciric type generalized F-contractions on complete metric spaces and fixed point results. Filomat 28(6), 1143–1151 (2014)
Rasham, T., Shoaib, A., Hussain, N.: Common fixed point results for new Ciric-type rational multivalued F-contraction with an application. J. Fixed Point Theory Appl. 20, 45 (2018). https://doi.org/10.1007/s11784-018-0525-6
Acknowledgements
This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
Funding
For this research article, funding is not applicable.
Author information
Authors and Affiliations
Contributions
P.S.K., V.V., and K.S.N. were involved with the organizing and execution of the study, as well as in the findings analysis and manuscript writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Panda, S.K., Vijayakumar, V. & Nisar, K.S. Applying periodic and anti-periodic boundary conditions in existence results of fractional differential equations via nonlinear contractive mappings. Bound Value Probl 2023, 91 (2023). https://doi.org/10.1186/s13661-023-01778-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-023-01778-3
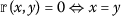 ;
;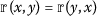 ;
;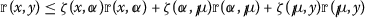
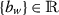 , we have
, we have  ,
, 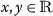 with
with 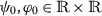 .
.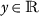 , where
, where 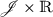 to
to 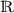 is continuous.
is continuous.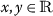 ,
, 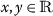 with
with 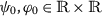 .
.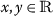 and
and 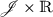 to
to  is continuous.
is continuous.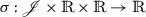 is continuous.
is continuous. ,
,  with
with 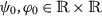 .
.