- Research
- Open access
- Published:
Remarks on a fractional nonlinear partial integro-differential equation via the new generalized multivariate Mittag-Leffler function
Boundary Value Problems volume 2023, Article number: 96 (2023)
Abstract
Introducing a new generalized multivariate Mittag-Leffler function which is a generalization of the multivariate Mittag-Leffler function, we derive a sufficient condition for the uniqueness of solutions to a brand new boundary value problem of the fractional nonlinear partial integro-differential equation using Banach’s fixed point theorem and Babenko’s technique. This has many potential applications since uniqueness is an important topic in many scientific areas, and the method used clearly opens directions for studying other types of equations and corresponding initial or boundary value problems. In addition, we use Python which is a high-level programming language efficiently dealing with the summation of multi-indices to compute approximate values of the generalized Mittag-Leffler function (it seems impossible to do so by any existing integral representation of the Mittag-Leffler function), and provide an example showing applications of key results derived.
1 Introduction
Partial differential equations have played an important role in various scientific areas, such as physics and engineering [1–8]. There are many interesting studies on uniqueness and existence of solutions, based on the theory of fixed points, for fractional nonlinear PDEs and corresponding initial or boundary value problems, as well as for integral equations [9, 10]. Ouyang and Zhu et al. [11–13] studied the time fractional PDEs given below:
where \(0 < \alpha \leq 1\), the function \(a(t)\) is a diffusion coefficient, l is a positive integer, \(\Omega \subset R^{l}\) is a bounded domain with a smooth boundary ∂Ω, \(\psi \in L^{2}(\Omega )\), and the function \(v: [0, T_{0}] \times R^{l} \rightarrow R\) satisfies certain conditions. Ouyang [11] investigated the existence of the local solutions using Leray–Schauder’s fixed point theorem. Additionally, Zhu et al. [12, 13] converted the above time fractional partial differential equations into a form of the time fractional differential equations in the Banach space \(L^{2}(\Omega )\), and, using Banach’s fixed point theorem and strict contraction principle, derived results on the existence and uniqueness.
Let \(a(x) \in C[0, T]\), \(g: [0, T] \times R \rightarrow R\), and \(f: C[0, T] \rightarrow R\). Very recently, Li [14] studied the uniqueness of solutions for the following nonlinear integro-differential equation with a nonlocal boundary condition and variable coefficients for \(l < \alpha \leq l + 1\):
where λ is a constant. In particular for \(l = 1\), equation (1.1) turns out to be
This paper aims to study the uniqueness of solutions for the following new equation with \(0 < \alpha \leq 1\) and \(m = 1, 2, \dots \), in the space \(S([0, 1]^{2} )\):
where all \(\lambda _{i}\) are constants, \(\psi (x)\) is a continuous function on \([0, 1]\), and \(v: [0, 1]^{2} \times R \rightarrow R\) is a function which satisfies conditions to be given. Equation (1.2) with its initial condition is new and, to the best of our knowledge, has never been investigated earlier.
The remainder of the paper is organized in the following manor. Section 3 studies the uniqueness of solutions for equation (1.2) by the newly introduced generalized multivariate Mittag-Leffler function and Banach’s fixed point theory. Section 4 presents a demonstrative example which illuminates applications of the key results based on the value of a generalized multivariate Mittag-Leffler function calculated by our Python code. Finally, in Sect. 5, we provide a summary of the work.
2 Preliminaries
We define \(I_{t}^{\alpha}\) as the partial Riemann–Liouville fractional integral of order \(\alpha > 0\) [15, 16] given by
and \(\frac{ _{c} \partial ^{\alpha}}{\partial t^{\alpha}}\) as the partial Liouville–Caputo fractional derivative of order \(\alpha > 0\) [15] by
From [17, 18], we have for \(0 < \alpha \leq 1\),
The set \(S([0, 1]^{2} )\) is a Banach space equipped with the following norm:
where u is continuous on \([0, 1]^{2}\).
Definition 1
A generalized multivariate Mittag-Leffler function is defined by the following series:
where \(\alpha _{i}, \epsilon, \delta > 0, \beta _{i} \geq 0, \zeta _{j} \in {\mathcal {C}} \) for \(1 \leq j \leq m\) and
In particular,
which is the multivariate Mittag-Leffler function given in [19] since \(\Gamma (1) = 1\). Moreover,
which is the well-known two-parameter Mittag-Leffler function.
Babenko’s approach [20] is a highly effective method that can be employed to solve various integral and differential equations [9, 17] by treating a bounded integral operator as a “normal” variable and using the inverse operator to deduce solutions. The method itself is similar to the Laplace transform while working on differential and integral equations with constant coefficients, but it can be applied to equations with continuous and bounded variable coefficients. To show this approach, we will consider the following equation in the space \(C[0, 1]\) (the space of all continuous functions on \([0, 1]\)) for constants a and b:
where
and
Obviously,
Applying \(I_{0}^{\alpha}\) to equation (2.1), we have
Considering the inverse operator of \((1 + a I_{0}^{\beta - \beta _{1}} + b I_{0}^{\beta + \alpha} )\), we informally get by Babenko’s technique
using
This implies that
which gives that the series solution
is an element in \(C[0, 1]\).
3 Uniqueness of solutions
Theorem 2
Let \(\psi \in C[0, 1]\), \(\lambda _{i}\) be real constants, \(\beta _{i}, \gamma _{i} \geq 0\) for all \(i = 1, 2, \dots, m\), and \(v: [0, 1]^{2} \times R \rightarrow R\) be a continuous and bounded function. In addition, we assume that \(0 < \alpha \leq 1\) and
Then \(u(t, x)\) is a solution to equation (1.2) if and only if it satisfies the following integral equation in the space \(S([0, 1]^{2} )\):
Furthermore,
Proof
Applying \(I_{t}^{\alpha}\) to equation (1.2), we get
This implies that
Using
we get
This further implies that
Using Babenko’s method, we deduce that
by the multinomial theorem. We will now show that \(u \in S([0, 1]^{2} )\). Indeed,
Since
we come to
since v is bounded. Hence \(u \in S([0, 1]^{2} )\). This marks the completion of the proof. □
Theorem 3
Let \(\psi \in C[0, 1]\), \(\lambda _{i}\) be real constants, \(\gamma _{i}, \beta _{i} \geq 0\) for all \(i = 1, 2, \dots, m\), and \(v: [0, 1]^{2} \times R \rightarrow R\) be a bounded and continuous function that satisfies the following Lipschitz condition for \({\mathcal {M}}> 0\):
Furthermore, we suppose that \(0 < \alpha \leq 1\) and
Then there is a unique solution in the space \(S([0, 1]^{2} )\) to equation (1.2).
Proof
Let \({\mathcal {T}}\) be the mapping defined on the space \(S([0, 1]^{2} )\) by
From the proof of Theorem 2, we claim that \({\mathcal {T}} u \in S([0, 1]^{2} )\). We will prove that \({\mathcal {T}}\) is contractive. In fact, for \(u_{1}, u_{2} \in S([0, 1]^{2} )\), we get from Theorem 2 that
by noting that
Since \(W < 1\), there is a unique solution to equation (1.2) in the space \(S([0, 1]^{2})\) by Banach’s fixed point theorem. Hence Theorem 3 follows. □
4 Example
Example 4
Consider the following equation with a boundary condition:
Then there is a unique solution in the space \(S([0, 1]^{2} )\) to equation (4.1).
Proof
Let
Obviously,
for all \(u_{1}, u_{2} \in R\), by noting that \((t, x) \in [0,1] \times [0, 1]\). Therefore \({\mathcal {M}} = 1/18\), and
from equation (4.1). We evaluate the following W given in Theorem 3 via Python language to get
By Theorem 3, the result follows. □
Remark 5
The Python language is quite useful when computing the values of the multivariate Mittag-Leffler function or the newly introduced generalized multivariate Mittag-Leffler function. These functions appear often in many fields and play an important role in studying integral or differential equations with various conditions, as well as in finding approximate solutions, such as for equation (2.1) as an example.
5 Conclusion
We have obtained a sufficient condition for uniqueness of solution to the new boundary value problem (1.2) involving double integral operators by using the new generalized multivariate Mittag-Leffler function, Babenko’s approach, as well as by applying Banach’s fixed point theorem. Moreover, we made use of the Python language to aid in finding the approximate value of a generalized Mittag-Leffler function, which currently seems unfeasible to do so by any existing integral representations of the Mittag-Leffler function. Finally, we presented an example that applies the results of the key theorems derived. The technique used certainly works for different types of PDE and corresponding initial or boundary value problems.
Availability of data and materials
No data were used to support this study.
Abbreviations
- \(I_{t}^{\alpha}\) :
-
the partial Riemann–Liouville fractional integral of order \(\alpha > 0\) with respect to t
- \(\frac{ _{c} \partial^{\alpha}}{\partial t^{\alpha}}\) :
-
, the partial Liouville–Caputo fractional derivative of order \(\alpha > 0\) with respect to t
-
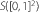 :
: -
the Banach space equipped with the following norm: \(\lVert u \rVert = \sup_{t \in [0, 1], x \in [0, 1]} |u(t, x)| \text{ for } u \in S([0, 1]^{2})\), where u is continuous on \([0, 1]^{2}\)
- \(E_{(\alpha_{1}, \ldots, \alpha_{m}), \, \epsilon}^{(\beta_{1}, \dots, \beta_{m}), \, \delta}(\zeta_{1}, \dots, \zeta_{m}) \) :
-
is the generalized multivariate Mittag-Leffler function
References
Atangana, A.: Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 102, 396–406 (2020)
Seadawy, A.R., Lu, D., Yue, C.: Travelling wave solutions of the generalized nonlinear fifth-order KdV water wave equations and its stability. J. Taibah Univ. Sci. 11, 623–633 (2017)
Rida, S.Z., El-Sherbinyb, H.M., Arafa, A.A.M.: On the solution of the fractional nonlinear Schrödinger equation. Phys. Lett. A 372, 553–558 (2008)
Marin, M., Agarwal, R.P., Mahmoud, S.R.: Modeling a microstretch thermoelastic body with two temperatures. Abstr. Appl. Anal. 2013, Article ID 583464 (2013)
Shannon, A.G., Özkan, E.: Some aspects of interchanging difference equation orders. Notes Number Theory Discrete Math. 28, 507–516 (2022)
Abo-Dahab, S.M., Abouelregal, A.E., Marin, M.: Generalized thermoelastic functionally graded on a thin slim strip non-Gaussian laser beam. Symmetry 12, 1094 (2020). https://doi.org/10.3390/sym12071094
Othman, M.I.A., Fekry, M., Marin, M.: Plane waves in generalized magneto-thermo-viscoelastic medium with voids under the effect of initial stress and laser pulse heating. Struct. Eng. Mech. 73, 621–629 (2020)
Bhatti, M.M., Shahid, A., Sarris, I.E., Bég, O.A.: Spectral relaxation computation of Maxwell fluid flow from a stretching surface with quadratic convection and non-Fourier heat flux using Lie symmetry transformations. Int. J. Mod. Phys. B 37, Article ID 2350082 (2023)
Li, C., Saadati, R., Allahviranloo, T.: Conditions to guarantee the existence of solutions for a nonlinear and implicit integro-differential equation with variable coefficients. Math. Methods Appl. Sci. (2022). https://doi.org/10.1002/mma.8890
Adjabi, Y., Jarad, F., Baleanu, D., Abdeljawad, T.: On Cauchy problems with Caputo–Hadamard fractional derivatives. J. Comput. Anal. Appl. 21, 661–681 (2016)
Ouyang, Z.G.: Existence and uniqueness of the solutions for a class of nonlinear fractional order partial differential equations with delay. Comput. Math. Appl. 61, 860–870 (2011)
Zhu, B., Liu, L.S., Wu, Y.H.: Local and global existence of mild solutions for a class of nonlinear fractional reaction–diffusion equations with delay. Appl. Math. Lett. 61, 73–79 (2016)
Zhu, B., Liu, L.S., Wu, Y.H.: Existence and uniqueness of global mild solutions for a class of nonlinear fractional reaction–diffusion equations with delay. Comput. Math. Appl. 78, 1811–1818 (2019)
Li, C.: Uniqueness of a nonlinear integro-differential equation with nonlocal boundary condition and variable coefficients. Bound. Value Probl. 2023, 26 (2023)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, North-Holland (2006)
Long, P., Murugusundaramoorthy, G., Tang, H., Wang, W.: Subclasses of analytic and bi-univalent functions involving a generalized Mittag-Leffler function based on quasi-subordination. J. Math. Comput. Sci. 26(4), 379–394 (2022)
Li, C.: Uniqueness of the partial integro-differential equations. J. Integral Equ. Appl. 22, 463–475 (2021)
Li, C., Saadati, R., Srivastava, R., Beaudin, J.: On the boundary value problem of nonlinear fractional integro-differential equations. Mathematics 10, Article ID 1971 (2022). https://doi.org/10.3390/math10121971.
Hadid, S.B., Luchko, Y.F.: An operational method for solving fractional differential equations of an arbitrary real order. Panam. Math. J. 6, 57–73 (1996)
Babenko, Y.I.: Heat and Mass Transfer. Khimiya, Leningrad (1986). (in Russian)
Acknowledgements
The authors thank the anonymous referees for their helpful comments that improved the quality of the manuscript.
Funding
This research is supported by the Natural Sciences and Engineering Research Council of Canada (Grant No. 2019-03907).
Author information
Authors and Affiliations
Contributions
CL, methodology, writing–original draft preparation. RS, supervision, and project administration. JB, editing, and writing–original draft preparation. AH, editing, and writing–original draft preparation. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, C., Saadati, R., Beaudin, J. et al. Remarks on a fractional nonlinear partial integro-differential equation via the new generalized multivariate Mittag-Leffler function. Bound Value Probl 2023, 96 (2023). https://doi.org/10.1186/s13661-023-01783-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-023-01783-6
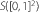 :
: