- Research
- Open access
- Published:
Infinite system of nonlinear tempered fractional order BVPs in tempered sequence spaces
Boundary Value Problems volume 2024, Article number: 23 (2024)
Abstract
This paper deals with the existence results of the infinite system of tempered fractional BVPs
where \(\mathtt{j}\in \mathbb{N}\), \(2<\varrho \le 3\), \(1<\mathtt{m}\le 2\), by utilizing the Hausdorff measure of noncompactness and Meir–Keeler fixed point theorem in a tempered sequence space.
1 Introduction
Fractional calculus is an important branch of mathematics that deals with the description of the possibility of computation of unknown functions via suitable derivative and integral operators of real order and studies the relationships between them [17, 19, 21]. The concept of fractional calculus has been widely used to model physical problems engineering systems, and their applications which significantly leads to a set of linear or nonlinear fractional differential equations [8, 35, 39, 42, 43]. The development of this discipline has inspired scholars to look into its existence and uniqueness [14, 28, 32–34, 38].
The tempered fractional derivative is obtained by multiplying the fractional derivative by an exponential factor. The traditional Riemann–Liouville (RL) and Caputo fractional derivatives are obtained under special circumstances for \(\uplambda =0\), and this new fractional operator depends on the parameter λ. Due to its use in physics, groundwater hydrology, poroelasticity, geophysical flow, and finance [7, 12, 13, 22, 23, 36], the tempered fractional derivative has recently gained popularity as a subject of study. In [44], Zaky studied the well-posedness of the solution to the following two-point nonlinear tempered fractional boundary value problem (TFBVP)
where \(\mathtt{g}\in \mathrm{C}([0,\mathrm{T}]\times \mathbb{R},\mathbb{R})\), α, β, γ are real constants with \(\upalpha +\upbeta \ne 0\), and \({}^{\mathfrak{c}}_{0}\mathrm{D}^{\upalpha ,{\uplambda}}_{\mathrm{r}}\) is the Caputo tempered fractional derivative of rational order \(\upalpha \in (0,1)\). Pandey et al. [29] by applying fractional variational approach, studied the properties of eigenvalues for the TFBVP
where ɸ, ϕ and \(\psi _{\upmu}\) are real-valued continuous functions defined on \([\upalpha ,\upbeta ]\). Recently, Khuddush and Prasad [15] studied the thermistor problem with two-point boundary conditions
where \(\uplambda \ge 0\), \(\upmu >0\), \({}^{\mathfrak{c}}\mathtt{D}^{2\varrho}_{0^{+}}\) denotes the tempered Caputo fractional derivative of order 2ϱ, \(\mathtt{g}\in \mathrm{C}([0,\mathtt{T}]\times \mathbb{R},\mathbb{R})\) and derived sufficient conditions for the existence, uniqueness and Hyers-Ulam stability of solutions.
The measure of noncompactness (MNC) plays a dominant role in functional analysis, as introduced by Kuratowski [18]. In [41], Srivastava et al. applied the MNC on \(\mathrm{C}([0, a]\times [0, a])\) to study the two variable functional integral equations. Many scholars have also used the notion of an MNC for the existence of solutions for results of infinite systems of differential and integral equations [2, 6, 10, 11, 25, 26, 30, 31, 40]. In the following, we mention a few recent works on MNC. By utilizing the Hausdorff measure of noncompactness (HMNC) in tempered sequence spaces, Das et al. [9] established the existence of solutions to the infinite system of TFBVP
where \(\mathtt{h}_{\mathtt{k}}\in \mathrm{C}([0,\mathrm{T}],\mathbb{R})\), and \({}^{\mathtt{R}}_{0}\mathrm{D}^{\upbeta}_{0^{+}}\) is a Riemann–Liouville fractional derivative of order \(\upbeta \in (1,2)\). Recently, Khuddush et al., [16] established the existence results by applying the concept of a family of measures of noncompactness in the space of functions \(\mathbb{C}^{\mathfrak{z},\upalpha}(\mathbb{R}^{+})\) to the following ∞-point fractional BVP
where m is a fixed nonnegative integer, \(\mathtt{c}_{\mathtt{j}}\in \mathbb{R}^{+}\), \(\varphi \in \mathrm{C}(\mathbb{R}^{+},\mathbb{R})\), \(\mathtt{h}\in \mathrm{C}(\mathbb{R}^{+}\times \mathbb{R},\mathbb{R})\). Inspired by the above-mentioned works, in this paper, we derive sufficient conditions for the existence of solutions via the HMNC in tempered sequence spaces to the following infinite system of TFBVP
where \(\mathtt{j}\in \mathbb{N}\), \(2<\varrho \le 3\), \(1<\mathtt{m}\le 2\), \(\uplambda >0\), \({}^{\mathtt{R}}_{0}\mathrm{D}^{\varrho ,{\uplambda}}_{\mathrm{r}}\) denotes the RL-tempered fractional derivative of order ϱ, \(\mathtt{z}(\mathrm{r})= (\mathtt{z}_{\mathtt{j}}(\mathrm{r}) )_{\mathtt{j}=1}^{\infty}\), and \(\psi _{\mathtt{j}}:(0,1)\to (0,1)\) is continuous. We also provide an example to illustrate the theoretical results.
2 Preliminaries
Essential results are stated here prior to proceeding to the main results in the subsequent sections.
-
Denote by \(\mathcal{AC}[\mathtt{b}, \mathtt{c}]\) the space of real-valued absolutely continuous functions \(\mathtt{z}(\mathrm{r})\) on \([\mathtt{b}, \mathtt{c}]\).
-
Denote by \(\mathcal{AC}^{k}[\mathtt{b}, \mathtt{c}]\) the space of real-valued functions \(\mathtt{z}(\mathrm{r})\), which have continuous derivatives of order \(k-1\) on \([\mathtt{b}, \mathtt{c}]\) such that \(\frac{\mathrm{d}^{k-1}\mathtt{z}(\mathrm{r})}{\mathrm{d}\mathrm{r}^{k-1}} \in \mathcal{AC}[\mathtt{b}, \mathtt{c}]\).
-
Denote by \(\mathcal{L}([\mathtt{b}, \mathtt{c}])\) the family of all Lebesgue measurable functions on \([\mathtt{b}, \mathtt{c}]\).
Definition 2.1
Let \(\mathtt{z}(\mathrm{r})\in \mathcal{L}([\mathtt{b}, \mathtt{c}])\), \(\uplambda \ge 0\) and \(\upeta >0\). The RL-tempered fractional integral of order η is defined as
where \({}^{\mathtt{R}}_{\mathtt{b}}\mathrm{I}^{\upeta}_{\mathrm{r}}\) is the classical RL-fractional integral [17]
Definition 2.2
Let \(k-1<\upeta <k\), \(k\in \mathbb{N}^{+}\) and \(\uplambda \ge 0\). The RL-tempered fractional derivative of order η is defined as
where \({}^{\mathtt{R}}_{\mathtt{b}}\mathrm{D}^{\upeta}_{\mathrm{r}}\) is the classical RL-fractional derivative [17]
Lemma 2.3
(Composite property [20]) Let \(\mathtt{z}(\mathrm{r})\in \mathcal{AC}^{k}[\mathtt{b}, \mathtt{c}]\) and \(k-1<\upeta <k\). Then, the composite property between RL-tempered fractional derivative and RL-tempered fractional integral is given by
and
To study the boundary value problem (1)–(2), first we solve the following linear fractional differential equation
satisfying the boundary conditions (2).
Lemma 2.4
Let z be a solution of (5) and (2) if and only if z solves the integral equation
where

and  .
.
Proof
Assume that \(\mathtt{z}\in C^{[\varrho ]+1}[0, 1] \) is a solution of (5). According to Lemma 2.3, we obtain
where \(\mathrm{A,B}\), and C are constants. Using the boundary condition \(\mathtt{z}(0)=0\), we get \(\mathrm{C}=0\), and hence
Applying the tempered fractional order derivative operator \({}^{\mathtt{R}}_{0}\mathrm{D}_{\mathrm{r}}^{\mathtt{m}, \uplambda}\) on both sides of (6), we get
Using condition \({}^{\mathtt{R}}_{0}\mathrm{D}_{\mathrm{r}}^{\mathtt{m}, \uplambda} \mathtt{z}(0)=0\), we obtain \(\mathtt{B}=0\). So, equation (6) reduced to
Taking \(\mathrm{r}=1\) into (7), (8) and using condition \(\mathtt{b}_{1} \mathtt{z}(1)+\mathtt{b}_{2} {}^{\mathtt{R}}_{0} \mathrm{D}_{\mathrm{r}}^{\mathtt{m}, \uplambda} \mathtt{z}(1)=0\), we get

Plugging A value into (8), we get

□
It is clear from Lemma 2.4 that \(\mathtt{z}_{\mathtt{j}}\) is a solution of (1)–(2) iff \(\mathtt{z}_{\mathtt{j}}\) solves the following integral equation
Lemma 2.5
Suppose that  , then for all \(\mathrm{r},\mathrm{p}\in [0,1]\), the kernel \(\mho (\mathrm{r},\mathrm{p})\) satisfies the following
, then for all \(\mathrm{r},\mathrm{p}\in [0,1]\), the kernel \(\mho (\mathrm{r},\mathrm{p})\) satisfies the following
-
(i)
\(\mho (\mathrm{r},\mathrm{p})\ge 0\) and continuous on \([0,1]\times [0,1]\).
-
(ii)
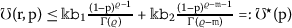 .
. -
(iii)
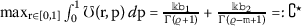 .
.
Proof
From the definition of \(\mho (\mathrm{r,p})\), it is clear that \(\mho (\mathrm{r,p})\) is continuous on \([0,1]\times [0,1]\). For \(\mathrm{r,p}\in [0,1]\), we have

This proves (i). For \(\mathrm{r,p}\in [0,1]\), we have

This proves (ii). Finally,

□
Definition 2.6
([18])
The Kurtowski MNC of F, where F is a subset of a metric space E, is given by
From above definition, we have
Let \(\mathrm{B}(\upzeta ,\mathtt{r})= \{\upxi \in \mathfrak{Z}: \Vert \upxi -\upzeta \Vert \le \mathtt{r} \}\), where \(\mathfrak{Z}\) is a Banach space equipped with the norm \(\Vert \cdot \Vert \).
Denote by \(\mathfrak{M}_{\mathfrak{Z}}\) the class of all non-empty and bounded subsets of \(\mathfrak{Z}\) and \(\mathfrak{N}_{\mathfrak{Z}}\) its subclass containing all relatively compact sets.
Definition 2.7
([4])
A real-valued function μ from \(\mathcal{M}_{\mathfrak{Z}}\) to \([0,1)\) is said to be an MNC if
-
(i)
\(\mathrm{K}\mathfrak{er}(\mu )= \{\mathrm{H}\in \mathfrak{M}_{ \mathfrak{Z}}:\mu (\mathrm{H})=0 \}\) is non-empty and \(\mathrm{K}\mathfrak{er}(\mu )\subset \mathcal{N}_{\mathfrak{Z}}\).
-
(ii)
\(\mu (\mathrm{H})\le \mu (\mathrm{G})\), if \(\mathrm{H}\subset \mathrm{G}\).
-
(iii)
\(\mu (\mathfrak{conv}(\mathrm{H}))=\mu (\mathrm{H})\), where \(\mathfrak{conv}(\mathrm{H})\) is the convex closure of H.
-
(iv)
\(\mu (\overline{\mathrm{H}})=\mu (\mathrm{H})\).
-
(v)
\(\mu (\upxi \mathrm{G}+(1-\upxi )\mathrm{H}) \le \xi \mu (\mathrm{G})+(1- \upxi )\mu (\mathrm{H})\) for all \(0\le \upxi \le 1\).
-
(vi)
if \(\mathrm{G}_{\mathrm{k}} \in \mathcal{M}_{\mathfrak{Z}}\), \(\mathrm{G}_{\mathrm{k}}=\overline{\mathrm{G}}_{\mathrm{k}}\), \(\mathrm{G}_{\mathrm{k}+1}\subset \mathrm{G}_{\mathrm{k}}\) for \(\mathrm{k}\in \mathbb{N}\) and \(\lim_{\mathrm{k} \to +\infty}\mu (\mathrm{G}_{ \mathrm{k}})=0\) then \(\bigcap_{\mathrm{k}=1}^{\infty} \mathrm{G}_{ \mathrm{k}} \ne \emptyset \).
Definition 2.8
([6])
The HMNC is defined as
where H is a bounded subset of a metric space G.
Next, we define some Banach spaces as
We also define
which is called the HMNC on the Banach space \((\mathtt{c}_{0},\Vert \cdot \Vert _{\mathtt{c}_{0}})\); for more details, see [6].
Definition 2.9
([27])
The MNC μ on the Banach space \((\mathtt{c},\Vert \cdot \Vert _{\mathtt{c}})\) is defined by
Definition 2.10
([5])
If \(\ell =(\ell _{\mathtt{j}})\), then ℓ is called a tempering sequence, if \(\ell _{\mathtt{j}}>0\) for all j and ℓ is nonincreasing. Define
Then, M is a linear space over \(\mathbb{R}\). We denote the space by \(\mathtt{c}^{\ell}_{0}\) and \(\mathtt{c}^{\ell}_{0}\) that is a Banach space with the norm \(\Vert \varpi \Vert _{\mathtt{c}^{\ell}_{0}}=\sup \{\ell _{ \mathrm{k}} \vert \varpi _{\mathrm{k}} \vert \}\). Next, let
Then, M is a linear space over \(\mathbb{R}\). We denote the space by \(\mathtt{c}^{\ell}\) and \(\mathtt{c}^{\ell}\) that is a Banach space with the norm \(\Vert \varpi \Vert _{\mathtt{c}^{\ell}}=\sup \{\ell _{ \mathrm{k}} \vert \varpi _{\mathrm{k}} \vert \}\).
Here, we note that there is a isometry between the spaces \(\mathtt{c}^{\ell}_{0}\) and \(\mathtt{c}_{0}\) and the spaces \(\mathtt{c}^{\ell}\) and c: In [5], the HMNC on \(\mathfrak{M}_{\mathtt{c}_{0}^{\ell}}\) is defined as
Also, the HMNC on \(\mathtt{c}^{\ell}\) is defined as
Let \(\mathtt{Q}=(0,1)\). Denote by \(\complement (\mathtt{Q},\mathtt{c}^{\ell}_{0})\) the space of all continuous functions on Q with values in \(\mathtt{c}^{\ell}_{0}\), which is a Banach space with the norm
Denote by \(\complement (\mathtt{Q},\mathtt{c}^{\ell})\) the space of all continuous functions on Q with values in \(c^{\ell}\), which is a Banach space with the norm
for more details, see [9].
Let \(\mathrm{G}\ne \emptyset \) be a bounded, closed and convex subset of \(\complement (\mathtt{Q},\mathtt{c}^{\ell})\) and \(\mathtt{z}\in \mathtt{Q}\) or \(\complement (\mathtt{Q},\mathtt{c}^{\ell}_{0})\), Then,
satisfy all the axioms of MNC on \(\complement (\mathtt{Q},\mathtt{c}^{\ell}_{0})\) and
satisfy all the axioms of MNC on \(\complement (\mathtt{Q},\mathtt{c}^{\ell})\), which can be found in [9].
Definition 2.11
([24])
Let G be a metric space with metric d. The mapping \(\mathtt{F}:\mathrm{G}\to \mathrm{G}\) is called a Meir–Keeler contraction if for any \(\updelta >0\), there exists \(\upeta >0\) such that
Theorem 2.12
([24])
Let G be a complete metric space. If \(\mathtt{F}:\mathrm{G}\to \mathrm{G}\) is a Meir–Keeler contraction, then F has a unique fixed point.
Definition 2.13
([1])
The mapping F on a non-empty subset U of a Banach space G is said to be a Meir–Keeler condensing operator if for any \(\upeta >0\), there exists \(\updelta >0\) such that
Theorem 2.14
In addition to Definition 2.13, if U is a closed, bounded and convex subset of G, then F has a fixed point.
3 Solvability of the Boundary Value Problem (1) in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\)
This portion deals with the existence of solutions for BVP (1) in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\).
We assume that the following conditions are met in this section:
-
(A)
Let \(\psi _{\mathtt{j}}:{\mathtt{Q}\times \mathbb{R}^{\infty}}\to { \mathbb{R}}\) and define an operator ψ from \(\mathtt{Q}\times \mathtt{c}^{\ell}_{0}\) to \(\mathtt{c}^{\ell}_{0}\) as \((\mathrm{r}, \mathtt{z}(\mathrm{r}))\to (\psi \mathtt{z})(\mathrm{r})= (\psi _{\mathtt{j}}(\mathrm{r}, \mathtt{z}(\mathrm{r})) )_{ \mathtt{j}=1}^{\infty}\), which is the family of all functions \(((\psi \mathtt{z})(\mathrm{r}) )_{\mathrm{r}\in \mathtt{Q}}\) equicontinuous on \(\mathtt{c}^{\ell}_{0}\).
-
(B)
\(\upxi _{\mathtt{j}}(\mathrm{r}), \upzeta _{\mathtt{j}}(\mathrm{r}): \mathtt{Q}\to \mathbb{R}\) are continuous functions, \(\ell _{\mathtt{j}}\upxi _{\mathtt{j}}(\mathrm{r}) \xrightarrow{{\text{uniformly}}}0\) converges on Q, and the sequence \((\upzeta _{\mathtt{j}}(\mathrm{r}))\) is equibounded on Q. Let \(\upzeta (\mathrm{r})=\sup \{\upzeta _{\mathtt{j}}(\mathrm{r}): \mathtt{j}\in \mathbb{N}\}\), \(\upzeta ^{\star }=\sup \{\upzeta (\mathrm{r}):\mathrm{r}\in \mathtt{Q}\}\), \(\ell ^{\star }=\sup \{\ell _{\mathtt{j}}\upxi _{\mathtt{j}}( \mathrm{r}):\mathtt{j}\in \mathbb{N},\mathrm{r}\in \mathtt{Q}\}\) and
$$ \bigl\vert \psi _{\mathtt{j}}\bigl(\mathrm{r},\mathtt{z}(\mathrm{r})\bigr) \bigr\vert \le \upxi _{\mathtt{j}}(\mathrm{r})+\upzeta _{\mathtt{j}}( \mathrm{r}) \bigl\vert \mathtt{z}_{\mathtt{j}}(\mathrm{r}) \bigr\vert , \quad \mathtt{z}_{\mathtt{j}}\in \mathtt{c}^{\ell}_{0},~ \mathrm{r}\in \mathtt{Q}, \mathtt{j}\in \mathbb{N}. $$
Theorem 3.1
Let \(\widehat{\mho}:=\sup_{\mathrm{p}\in \mathtt{Q}}\mho ^{\star}( \mathrm{p})\), and suppose \(e^{\uplambda}\widehat{\mho}<1\) and \((\mathrm{A})-(\mathrm{B})\) hold, then BVP (1) has at least one solution \(\mathtt{z}(\mathrm{r})= (\mathtt{z}_{\mathtt{j}} (\mathrm{r}) )_{\mathtt{j}=1}^{\infty}\) in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\).
Proof
Since \(\sup \{\ell _{\mathtt{j}}\vert \mathtt{z}_{\mathtt{j}}(\mathrm{r}) \vert \}<+\infty \) for all \(\mathtt{z}(\mathrm{r})= (\mathtt{z}_{\mathtt{j}}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\in \complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\) and \(\mathrm{r}\in \mathtt{Q} \exists \kappa >0\ni \) \(\sup \{\ell _{\mathtt{j}}\vert \mathtt{z}_{\mathtt{j}}(\mathrm{r}) \vert \}<\kappa \). From \((\mathrm{B})\) and (9), we get
Therefore,
Let \(\mathcal{E}=\mathcal{E}(\mathtt{z}^{0}(\mathrm{r}),a_{1})\) be a closed ball centered at \(\mathtt{z}^{0}(\mathrm{r})= (\mathtt{z}^{0}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\), for all \(\mathrm{r}\in \mathtt{Q}\), and radius \(a_{1}\). So, \(\mathcal{E}\) is a non-empty closed, bounded and convex subset of \(\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\).
For fixed \(\mathrm{r}\in \mathtt{Q}\), define an operator \(\wp =(\wp _{\mathtt{j}})_{\mathtt{j}=1}^{\infty}:\complement ( \mathtt{Q}, \mathtt{c}^{\ell}_{0})\to \complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\) as
Since \((\psi _{\mathtt{j}}(\mathrm{r}, \mathtt{z}(\mathrm{r})) )_{ \mathtt{j}=1}^{\infty}\in \mathtt{c}^{\ell}_{0}\), for \(\mathrm{r}\in \mathtt{Q}\), it follows that
Thus, \((\wp \mathtt{z})(\mathrm{r})\in \complement (\mathtt{Q}, \mathtt{c}^{ \ell}_{0})\). It is easy to see that \((\wp _{\mathtt{j}}\mathtt{z})(\mathrm{r})\) satisfies
For fixed \(\mathrm{r}\in \mathtt{Q}\) and \(\mathtt{z}(\mathrm{r})\in \mathcal{E}\), we get
Thus, ℘ is a self-mapping on \(\mathcal{E}\). From \((\mathrm{A})\), for any \(\mathtt{z}(\mathrm{r})= (\mathtt{z}_{\mathtt{j}}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\in \mathcal{E}\) and for any \(\upeta >0\), there exists \(\upxi >0\) such that \(\Vert (\psi \mathtt{z})(\mathrm{r})-(\psi \mathtt{w})(\mathrm{r}) \Vert _{\mathtt{c}^{\ell}_{0}}< \frac {\upeta}{e^{\uplambda}\widehat{\mho}}\) for each \(\mathtt{z}(\mathrm{r})\in \mathcal{E}\), whenever \({\vert \mathtt{z}(\mathrm{r})-\mathtt{w}(\mathrm{r}) \vert}\le \upxi \), where \(\mathrm{r}\in \mathtt{Q}\). So, for \(\mathrm{r}\in \mathtt{Q}\), we have
Thus, ℘ is continuous on \(\mathcal{E} \forall \mathrm{r}\in \mathtt{Q}\).
Now, we have
Thus,
It follows that
That is
Setting \(\upxi =\frac{\upeta}{e^{\uplambda}\widehat{\mho}} [1-e^{\uplambda}\widehat{\mho} ]\), we get \(\upeta \le \chi _{\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})}( \mathcal{E})<\upeta +\upxi \).
Therefore, ℘ is a Meir–Keeler condensing operator on \(\mathcal{E}\). Further, ℘ satisfies all the conditions of Theorem 2.14, i.e., ℘ has a fixed point in \(\mathcal{E}\). Hence, BVP (1) has a solution in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\). □
4 Solvability of the BVP (1) in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell})\)
In this section, we study the solvability of BVP (1) in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell})\).
We assume the following conditions hold throughout this section:
-
(C)
Let \(\psi _{\mathtt{j}}:{\mathtt{Q}\times \mathbb{R}^{\infty}\to \mathbb{R}}\) and define an operator ψ from \(\mathtt{Q}\times \mathtt{c}^{\ell}\) to \(\mathtt{c}^{\ell}\) as \((\mathrm{r}, \mathtt{z}(\mathrm{r}))\to (\psi \mathtt{z})(\mathrm{r})= (\psi _{\mathtt{j}}(\mathrm{r}, \mathtt{z}(\mathrm{r})) )_{ \mathtt{j}=1}^{\infty}\), which is the family of all functions \(((\psi \mathtt{z})(\mathrm{r}) )_{\mathrm{r}\in \mathtt{Q}}\) equicontinuous on \(\mathtt{c}^{\ell}\).
-
(D)
\(\upeta _{\mathtt{j}}(\mathrm{r}), \mathfrak{z}_{\mathtt{j}}( \mathrm{r}):\mathtt{Q}\to \mathbb{R}\) are continuous functions such that the sequence \(\ell _{\mathtt{j}}\upeta _{\mathtt{j}}(\mathrm{r}) \xrightarrow{\text{uniformly}}0\) on Q and the sequence \((\mathfrak{z}_{\mathtt{j}}(\mathrm{r}))\) is convergence on Q, so we take \(\mathfrak{z}(\mathrm{r})=\sup \{\mathfrak{z}_{\mathtt{j}}(\mathrm{r}): \mathtt{j}\in \mathbb{N}\}\), \(\mathfrak{z}^{\star }=\sup \{\mathfrak{z}(\mathrm{r}):\mathrm{r}\in \mathtt{Q}\}\), \(\ell ^{\star }=\sup \{\ell _{\mathtt{j}}\upeta _{\mathtt{j}}( \mathrm{r}):\mathtt{j}\in \mathbb{N},\mathrm{r}\in \mathtt{Q}\}\) and
$$ \psi _{\mathtt{j}}\bigl(\mathrm{r},\mathtt{z}(\mathrm{r})\bigr)\le \upeta _{ \mathtt{j}}(\mathrm{r})+\mathfrak{z}_{\mathtt{j}}(\mathrm{r}) \mathtt{z}_{\mathtt{j}}(\mathrm{r}), \quad \mathtt{z}_{\mathtt{j}}\in \mathtt{c}^{\ell},~\mathrm{r}\in \mathtt{Q}, \mathtt{j}=1,2,3,\ldots . $$
Theorem 4.1
Let \(\widehat{\mho}:=\sup_{\mathrm{p}\in \mathtt{Q}}\mho ^{\star}( \mathrm{p})\), suppose \(e^{\uplambda}\widehat{\mho}\mathfrak{z}^{\star}<1\) and \((\mathscr{C})\)–\((\mathscr{D})\) hold, then BVP (1) has at least one solution \(\mathtt{z}(\mathrm{r})= (\mathtt{z}_{\mathtt{j}}(\mathrm{r}) )\) in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell})\).
Proof
Since \(\sup \{\ell _{\mathtt{j}}\vert \mathtt{z}_{\mathtt{j}}(\mathrm{r}) \vert \}<+\infty \) for all \(\mathtt{z}(\mathrm{r})= (\mathtt{z}_{\mathtt{j}}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\in \complement (\mathtt{Q}, \mathtt{c}^{\ell})\) and \(\mathrm{r}\in \mathtt{Q}\), there exists \(\uprho >0\) such that \(\sup \{\ell _{\mathtt{j}}\vert \mathtt{z}_{\mathtt{j}}(\mathrm{r}) \vert \}<\uprho \). From \((\mathrm{D})\) and (9), we get
Thus,
Let \(\mathcal{S}=\mathcal{S}(\mathtt{z}^{0}(\mathrm{r}),r_{1})\) be closed with center \(\mathtt{z}^{0}(\mathrm{r})= (\mathtt{z}^{0}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\) for all \(\mathrm{r}\in \mathtt{Q}\) and radius b. So, \(\mathcal{S}\) is a non-empty bounded, closed convex subset of \(\complement (\mathtt{Q}, \mathtt{c}^{\ell})\).
For fixed \(\mathrm{r}\in \mathtt{Q}\), define an operator \(\pounds =(\pounds _{\mathtt{j}})_{\mathtt{j}=1}^{\infty}: \complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\to \complement ( \mathtt{Q}, \mathtt{c}^{\ell}_{0})\) as
Now, let \(\mathtt{i}\in \mathbb{N}\) and
Observe that
As \(\mathtt{j,i}\to \infty \), we obtain \(\vert \mathfrak{z}_{\mathtt{j}}(\mathrm{p})-\mathfrak{z}_{\mathtt{i}}( \mathrm{p})\vert \to 0\), \(\vert \ell _{\mathtt{j}}\mathtt{z}_{\mathtt{j}}(\mathrm{p})-\ell _{ \mathtt{i}}\mathtt{z}_{\mathtt{i}}(\mathrm{p})\vert \to 0\) and \(\vert \ell _{\mathtt{j}}\upeta _{\mathtt{j}}(\mathrm{p})-\ell _{ \mathtt{i}}\upeta _{\mathtt{i}}(\mathrm{p})\vert \to 0\). Since \((\mathfrak{z}_{\mathtt{j}})\), \((\ell _{\mathtt{j}}\upeta _{\mathtt{j}})\) are convergent on Q and \(\mathtt{z}_{\mathtt{j}}(\mathrm{p})\in \complement (\mathtt{Q}, \mathtt{c}^{\ell})\), it follows that
Hence, \((\pounds \mathtt{z})(\mathrm{r})\in \complement (\mathtt{Q}, \mathtt{c}^{\ell})\). We also note that \((\pounds _{\mathtt{j}}\mathtt{z})(\mathrm{r})\) satisfies
For fixed \(\mathrm{r}\in \mathtt{Q}\) and \(\mathtt{z}(\mathrm{r})\in \mathcal{S}\), we get
which proves that £ is a self-mapping on \(\mathcal{S}\). From \((\mathrm{C})\), for any \(\mathtt{w}(\mathrm{r})= (\mathtt{w}_{\mathtt{j}}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\in \mathcal{S}\) and for any \(\upeta >0\), there exists \(\upxi >0\) such that \(\Vert (\psi \mathtt{z})(\mathrm{r})-(\psi \mathtt{w})(\mathrm{r}) \Vert _{\mathtt{c}^{\ell}}< \frac {\upeta}{e^{\uplambda}\widehat{\mho}}\) for each \(\mathtt{z}(\mathrm{r})\in \mathcal{S}\), whenever \(\vert \mathtt{z}(\mathrm{r})-\mathtt{w}(\mathrm{r}) \vert\le \upxi \), where \(\mathrm{r}\in \mathtt{Q}\). So, for \(\mathrm{r}\in \mathtt{Q}\), we have
So, £ is continuous on \(\mathcal{S}\) for every \(\mathrm{r}\in \mathtt{Q}\).
Now, we have
Thus,
It follows that,
Setting \(\upxi = \frac{\upeta}{e^{\uplambda}\widehat{\mho}\mathfrak{z}^{\star}} [1-e^{ \uplambda}\widehat{\mho}\mathfrak{z}^{\star} ]\), we get \(\upeta \le \upmu _{\complement (\mathtt{Q}, \mathtt{c}^{\ell})}( \mathcal{S})<\upeta +\upxi \).
Therefore, £ is a Meir–Keeler condensing operator on \(\mathcal{S}\). Since r is arbitrary, so for every \(\mathrm{r}\in \mathtt{Q}\), £ satisfies all the conditions of Theorem 2.14, i.e., £ has a fixed point in \(\mathcal{S}\). Hence, BVP (1) has a solution in \(\complement (\mathtt{Q}, \mathtt{c}^{\ell})\). □
5 Applications
In this section, we provide two examples to check the validity of our main results.
Example 5.1
Consider the following BVP
So, \(\varrho =\frac{5}{2}\), \(\mathtt{m}=\frac{3}{2}\), \(\uplambda =\frac{1}{6}\), \(\mathtt{b}_{1}=0.1\), \(\mathtt{b}_{2}=\frac{2}{3\sqrt{\uppi}}\), \(\mathtt{Q}=[0, 1]\), and \(\psi _{\mathtt{j}}(\mathrm{r},\mathtt{z}(\mathrm{r}))= \frac{e^{-\mathtt{j}\mathrm{r}}\cos (\mathtt{j}\mathrm{r})}{\mathtt{j}} +\sum_{\mathrm{i}=\mathtt{j}}^{\infty} \frac{\mathtt{z}_{\mathtt{j}}(\mathrm{r})}{\mathrm{i}^{2}}\).
Let \(\ell _{\mathtt{j}}=\frac{1}{\mathtt{j}}\) for all \(\mathtt{j}\in \mathbb{N}\). Now, for \(\mathtt{z}(\mathrm{r})\in \complement (\mathtt{Q},\mathtt{c}_{0}^{ \ell})\), we have
Next, let \(\upnu (\mathrm{r})= (\nu _{\mathtt{j}}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\in \complement (\mathtt{Q},\mathtt{c}_{0}^{ \ell})\). Let \(\upeta >0\) be given and \(\updelta =\frac{24\upeta}{\uppi ^{2}}\) such that \(\Vert \mathtt{z}(\mathrm{r})-\upnu (\mathrm{r})\Vert _{\complement ( \mathtt{Q},\mathtt{c}_{0}^{\ell})}<\updelta \). Then,
Thus, \(((\psi \mathtt{z})(\mathrm{r}))_{\mathrm{r}\in \mathtt{Q}}\) is equicontinuous on \({\mathtt{c}^{\ell}_{0}}\). For \(\mathrm{r}\in \mathtt{Q}\) and \(\mathtt{j}\in \mathbb{N}\), we also have
where \(\upxi _{\mathtt{j}}(\mathrm{r})=\frac{1}{\mathtt{j}}\) and \(\upzeta _{\mathtt{j}}(\mathrm{r})=\frac{\uppi ^{2}}{6}\). So, \(\upzeta ^{\star }=\frac{\uppi ^{2}}{6}\). We note that \((\ell \upxi _{\mathtt{j}}(\mathrm{r}) )= (1/\mathtt{j}^{2} )\xrightarrow{\text{uniformly}} 0\) on Q, and the sequence \(\upzeta _{\mathtt{j}}(\mathrm{r})\) is equibounded on Q. Also,  ,
,

Then, \(\widehat{\mho}=0.754\). So,
Hence, by Theorem 3.1, BVP (11)–(12) has a solution in \(\complement (\mathtt{Q},\mathtt{c}^{\ell}_{0})\).
Example 5.2
Consider the BVP
So, \(\varrho =\frac{7}{3}\), \(\mathtt{m}=\frac{4}{3}\), \(\uplambda =\frac{1}{8}\), \(\mathtt{Q}=[0, 1]\), \(\mathtt{b}_{1}=0.2\), \(\mathtt{b}_{2}=\frac{27}{4\sqrt{3}\uppi}\), and \(\psi _{\mathtt{j}}(\mathrm{r},\mathtt{z}(\mathrm{r}))= \frac{1}{\mathtt{j}} +\sum_{\mathrm{i}=\mathtt{j}}^{\infty} \frac{\mathtt{z}_{\mathtt{j}}(\mathrm{r})}{2\mathrm{i}^{2}}\).
Let \(\ell _{\mathtt{j}}=\frac{1}{\mathtt{j}}\) for all \(\mathtt{j}\in \mathbb{N}\). Now, for \(\mathtt{z}(\mathrm{r})\in \complement (\mathtt{Q},\mathtt{c}^{\ell})\), we have
This shows that \((\psi _{\mathtt{j}}(\mathrm{r},\mathtt{z}(\mathrm{r})) )\in \mathtt{c}^{\ell}\). Next, let \(\mathtt{w}(\mathrm{r})= (\mathtt{w}_{\mathtt{j}}(\mathrm{r}) )_{ \mathtt{j}=1}^{\infty}\in \complement (\mathtt{Q},\mathtt{c}^{\ell})\). Let \(\upeta >0\) be given and \(\updelta =\frac{12\upeta}{\uppi ^{2}}\) such that \(\Vert \mathtt{z}(\mathrm{r})-\mathtt{w}(\mathrm{r})\Vert _{ \complement (\mathtt{Q},\mathtt{c}^{\ell})}<\upxi \). Then
Thus, \(((\psi \mathtt{z})(\mathrm{r}))_{\mathrm{r}\in \mathtt{Q}}\) is equicontinuous on \({\mathtt{c}^{\ell}}\). For \(\mathrm{r}\in \mathtt{Q}\) and \(\mathtt{j}\in \mathbb{N}\), we also have \(\upeta _{\mathtt{j}}(\mathrm{r})=\frac{1}{\mathtt{j}}\) and \(\mathfrak{z}_{\mathtt{j}}(\mathrm{r})= \frac{\pi ^{2}}{12}\). So, \(\mathfrak{z}^{\star }=\frac{\uppi ^{2}}{12}\). We note that \((\ell \upeta _{\mathtt{j}}(\mathrm{r}) )= (\frac{1}{\mathtt{j}^{2}} )\xrightarrow{\text{uniformly}}0\) on Q, and the sequence \(\mathfrak{z}_{\mathtt{j}}(\mathrm{r})\) is convergent on Q. Also,  ,
,

Then, \(\widehat{\mho}=0.84\). So,
Hence, by Theorem 4.1, BVP (13)–(14) has a solution in \(\complement (\mathtt{Q},\mathtt{c}^{\ell})\).
6 Conclusion
The present paper considers a boundary value problem with an infinite system of tempered fractional order. A variation of the well-known RL-fractional derivative, the so-called tempered fractional RL-derivative, is the fractional derivative used in our case. Using the HMNC technique and the Meir–Keeler fixed point theorem, we looked into whether there is a solution to an infinite system. This study was conducted in two brand-new sequence spaces: tempered sequence spaces \(\complement (\mathtt{Q}, \mathtt{c}^{\ell}_{0})\) and \(\complement (\mathtt{Q},\mathtt{c}^{\ell})\). Finally, numerical examples are also given to demonstrate the results we achieved. Future research could focus on the following areas:
-
(1)
To investigate infinite system of singular TFBVP, further research is required.
-
(2)
Is it possible to expand the concept used in this paper to investigate infinite systems of fractional difference equations and dynamic equations on time scales.
References
Aghajani, A., Mursaleen, M., Haghighi, A.S.: Fixed point theorems for Meir–Keeler condensing operators via MNC. Acta Math. Sci. 35(3), 552–566 (2015)
Alotaibi, A., Mursaleen, M., Mohiuddine, S.A.: Application of MNC to infinite system of linear equations in sequence spaces. Bull. Iranian Math. Soc. 41, 519–527 (2015)
Bai, Z., Lu, H.: Positive solutions for a boundary value problem of nonlinear fractional differential equations. J. Math. Anal. Appl. 311, 495–505 (2005)
Banas, J.: On measures of noncompactness in Banach spaces. Comment. Math. Univ. Carol. 21, 131–143 (1980)
Banas, J., Krajewska, M.: Existence of solutions for infinite systems of differential equations in spaces of tempered sequences. Electron. J. Differ. Equ. 2017, 60 (2017)
Banas, J., Mursaleen, M.: Sequence Spaces and Measures of Noncompactness with Applications to Differential and Integral Equations. Springer, New Delhi (2014)
Cartea, A., Castillo-Negrete, D.D.: Fractional diffusion models of option prices in markets with jumps. Phys. A, Stat. Mech. Appl. 374(2), 749–763 (2007)
Cichon, M., Salem, H.A.H.: On the lack of equivalence between differential and integral forms of the Caputo-type fractional problems. J. Pseudo-Differ. Oper. Appl. 11, 1869–1895 (2020)
Das, A., Hazarika, B., Agarwal, R.P., Nashine, H.K.: Solvability of infinite systems of fractional differential equations in the spaces of tempered sequences. Filomat 33(17), 5519–5530 (2019)
Das, A., Hazarika, B., Mahato, N.K., Parvaneh, V.: Application of measure of noncompactness on integral equations involving generalized proportional fractional and Caputo-Fabrizio fractional integrals. Filomat 36(17), 5885–5893 (2022). https://doi.org/10.2298/FIL2217885D
Das, P., Paunovic, M., Parvaneh, V., Mursaleen, M., Bagheri, Z.: Existence of a solution to an infinite system of weighted fractional integral equations of a function with respect to another function via a measure of noncompactness. Demonstr. Math. 56, 20220192 (2023)
Hanyga, A.: Wave propagation in media with singular memory. Math. Comput. Model. 34(12–13), 1399–1421 (2001)
He, J.Q., Dong, Y., Li, S.T., Liu, H.L., Yu, Y.J., Jin, G.Y., Liu, L.D.: Study on force distribution of the tempered glass based on laser interference technology. Optik 126(24), 5276–5279 (2015)
Khuddush, K., Prasad, K.R.: Infinitely many positive solutions for an iterative system of conformable fractional order dynamic boundary value problems on time scales. Turk. J. Math. 46, 433–452 (2022). https://doi.org/10.3906/mat-2106-110
Khuddush, M., Prasad, K.R.: Existence, uniqueness and stability analysis of a tempered fractional order thermistor boundary value problems. J. Anal. 31, 85–107 (2023). https://doi.org/10.1007/s41478-022-00438-6
Khuddush, M., Prasad, K.R., Leela, D.: Existence of solutions to the ∞-point fractional BVP posed on half-line via a family of MNC in the Hölder space \(C^{\varrho ,\upalpha}(R^{+})\). Filomat 36(10), 3527–3543 (2022). https://doi.org/10.2298/FIL2210527K
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier, North Holland (2006)
Kuratowski, K.: Sur les espaces completes. Fundam. Math. 15, 301–309 (1930)
Li, C., Cai, M.: Theory and numerical approximations of fractional integrals and derivatives. J. Soc. Ind. Appl. Math. (2019)
Li, C., Deng, W., Zhao, L.: Well-posedness and numerical algorithm for the tempered fractional ordinary differential equations. Discrete Contin. Dyn. Syst. 24(4), 1989–2015 (2019)
Mainardy, F.: Fractional Calculus and Waves in Linear Viscoelasticity. Imperial College Press, London (2002)
Meerschaert, M.M., Sabzikar, F., Phanikumar, M.S., Zeleke, A.: Tempered fractional time series model for turbulence in geophysical flows. J. Stat. Mech. Theory Exp. 2014(9), P09023 (2014)
Meerschaert, M.M., Zhang, Y., Baeumer, B.: Tempered anomalous diffusion in heterogeneous systems. Geophys. Res. Lett. 35(17), 1–5 (2008)
Meir, A., Keeler, E.: A theorem on contraction mappings. J. Math. Anal. Appl. 28, 326–329 (1969)
Mursaleen, M., Bilal, B., Rizvi, S.M.H.: Applications of MNC to infinite system of fractional differential equations. Filomat 31(11), 3421–3432 (2017)
Mursaleen, M., Mohiuddine, S.A.: Applications of measures of noncompactness to the infinite system of differential equations in \(\varrho _{p}\) spaces. Nonlinear Anal. 75, 2111–2115 (2012)
Mursaleen, M., Rizvi, S.M.H., Samet, B.: Solvability of a class of boundary value problems in the space of convergent sequences. Appl. Anal. 97(11), 1829–1845 (2018)
Muthaiah, S., Baleanu, D., Thangaraj, N.G.: Existence and Hyers-Ulam type stability results for nonlinear coupled system of Caputo-Hadamard type fractional differential equations. AIMS Math. 6(1), 168–194 (2021)
Pandey, P.K., Pandey, R.K., Yadav, S., Agrawal, O.P.: Variational approach for tempered fractional Sturm-Liouville problem. Int. J. Appl. Comput. Math. 7, 51 (2021). https://doi.org/10.1007/s40819-021-01000-x
Parvaneh, V., Banaei, S., Roshan, J.R., Mursaleen, M.: On tripled fixed point theorems via measure of noncompactness with applications to a system of fractional integral equations. Filomat 35(14), 4897–4915 (2021)
Paunovic, M., Mohammadi, B., Parvaneh, V.: On weak Wardowski contractions and solvability of p-Caputo implicit fractional pantograph differential equation with generalized anti-periodic boundary conditions. J. Nonlinear Convex Anal. 23(6), 1261–1274 (2022)
Prasad, K.R., Khuddush, M., Leela, D.: Existence of solutions for infinite systems of regular fractional Sturm-Liouville problems in the spaces of tempered sequences. Tbil. Math. J. 13(4), 193–209 (2020). https://doi.org/10.32513/tbilisi/1608606058
Prasad, K.R., Khuddush, M., Veeraiah, P.: Countably many positive solutions for singular R-L fractional order bvp with R-S integral boundary conditions. Nonlinear Stud. 27(4), 1075–1089 (2020)
Rabbani, M., Das, A., Hazarika, B., Arab, R.: MNC of a new space of tempered sequences and its application on fractional differential equations. Chaos Solitons Fractals 140, 110221 (2020)
Recent, D.L.: Applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. (2003). https://doi.org/10.1155/S0161171203301486
Rosenau, P.: Tempered diffusion: a transport process with propagating fronts and inertial delay. Phys. Rev. A 46(12), R7371 (1992)
Sabzikar, F., Meerschaert, M.M., Chen, J.: Tempered fractional calculus. J. Comput. Phys. 293, 14–28 (2015)
Salem, A., Alshehri, H.M., Almaghamsi, L.: MNC for an infinite system of fractional Langevin equation in a sequence space. Adv. Differ. Equ. 2021, 132 (2021). https://doi.org/10.1186/s13662-021-03302-2
Srivastava, H.M.: Diabetes and its resulting complications: mathematical modeling via fractional calculus. Public Health Open Access 4(3), 1–5 (2020)
Srivastava, H.M., Das, A., Hazarika, B., Mohiuddine, S.A.: Existence of solutions of infinite systems of differential equations of general order with boundary conditions in the spaces \(c_{0}\) and \(\varrho _{1}\) via the MNC. Math. Methods Appl. Sci. 41(10), 3558–3569 (2018)
Srivastava, H.M., Das, A., Hazarika, B., Mohiuddine, S.A.: Existence of solution for non-linear functional integral equations of two variables in Banach algebra. Symmetry 11, 1–16 (2019)
Srivastava, H.M., Saad, K.M., Khader, M.M.: An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals 140, 1–7 (2020)
Tarasov, V.E., Tarasova, V.V.: Time dependent fractional dynamics with memory in quantum and economic physics. Ann. Phys. 383, 579–599 (2017)
Zaky, M.A.: Existence, uniqueness and numerical analysis of solutions of tempered fractional boundary value problems. Appl. Numer. Math. 145, 429–457 (2019)
Acknowledgements
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number ISP-2024.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rao, S.N., Khuddush, M., Msmali, A.H. et al. Infinite system of nonlinear tempered fractional order BVPs in tempered sequence spaces. Bound Value Probl 2024, 23 (2024). https://doi.org/10.1186/s13661-024-01826-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-024-01826-6
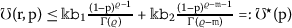 .
.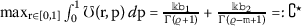 .
.